Codeforces Round #226 (Div. 2)

u010660276發表於2014-02-02

A. Bear and Raspberry

思路:只要找到前一個比後一個差值的最大值就可以。

#include<iostream>
#include<cstdio>
using namespace std;
int main()
{
    //freopen("in.txt","r",stdin);
    int n,k,x,y;
    int ans=0;
    cin>>n>>k>>x;
    for(int i=1;i<n;i++)
    {
        cin>>y;
        if(y<x&&x-y>ans)ans=x-y;
        x=y;
    }
    cout<<(ans-k<=0?0:ans-k)<<endl;
    return 0;
}

B. Bear and Strings

題意：找出所有的i，j，使得處於ij之間的子序列至少含有一個bear。

思路：每次匹配一個後找到從當前x到上一個匹配的距離*到最後的距離，所以每次儲存上一個匹配的位置

#include<iostream>
#include<string>
#include<cstdio>
using namespace std;
string a,b("bear");
int main()
{
    //freopen("in.txt","r",stdin);
    cin>>a;
    int before=-1,ans=0,len=a.size();
    if(len<4){cout<<0<<endl;return 0;}
    for(int i=0;i<len;i++)
    {
        bool flag=true;
        for(int j=0;j<4;j++)
            if(a[i+j]!=b[j]){flag=false;break;}

        if(!flag)continue;
        //cout<<i<<endl;
        ans+=(i-before)*(len-i-3);
        before=i;
    }
    cout<<ans<<endl;
    return 0;
}

C. Bear and Prime Numbers
time limit per test
2 seconds
memory limit per test
512 megabytes
input
standard input
output
standard output

Recently, the bear started studying data structures and faced the following problem.

You are given a sequence of integers x1, x2, ..., xn of length n and m queries, each of them is characterized by two integers li, ri. Let's introduce f(p) to represent the number of such indexes k, that xk is divisible by p. The answer to the query li, ri is the sum: 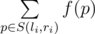, where S(li, ri) is a set of prime numbers from segment [li, ri] (both borders are included in the segment).

Help the bear cope with the problem.

Input

The first line contains integer n (1 ≤ n ≤ 106). The second line contains n integers x1, x2, ..., xn (2 ≤ xi ≤ 107). The numbers are not necessarily distinct.

The third line contains integer m (1 ≤ m ≤ 50000). Each of the following m lines contains a pair of space-separated integers, li and ri (2 ≤ li ≤ ri ≤ 2·109) — the numbers that characterize the current query.

Output

Print m integers — the answers to the queries on the order the queries appear in the input.

Sample test(s)
Input
6
5 5 7 10 14 15
3
2 11
3 12
4 4
Output
9
7
0
Input
7
2 3 5 7 11 4 8
2
8 10
2 123
Output
0
7
Note

Consider the first sample. Overall, the first sample has 3 queries.

  1. The first query l = 2, r = 11 comes. You need to count f(2) + f(3) + f(5) + f(7) + f(11) = 2 + 1 + 4 + 2 + 0 = 9.
  2. The second query comes l = 3, r = 12. You need to count f(3) + f(5) + f(7) + f(11) = 1 + 4 + 2 + 0 = 7.
  3. The third query comes l = 4, r = 4. As this interval has no prime numbers, then the sum equals 0.

寫起來較噁心，1900飄過。。。

打素數表然後判斷數字能被那些素數整除。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxm=10000005;
int prime[maxm],cnt[maxm];
bool is_prime[maxm];
int n,m,num;
void make_prime_table()
{
    num=0;
    fill(is_prime,is_prime+maxm,1);
    is_prime[0]=is_prime[1]=false;
    for(int i=2; i<maxm; i++)
    {
        if(is_prime[i])
        {
            prime[num++]=i;
            for(int j=2*i; j<maxm; j+=i)is_prime[j]=false;
        }
    }
}
int main()
{
    //freopen("in.txt","r",stdin);
    make_prime_table();
    scanf("%d",&n);
    int x,l,r;
    memset(cnt,0,sizeof(cnt));
    for(int i=1; i<=n; i++)
    {
        scanf("%d",&x);
        if(is_prime[x])
            cnt[x]++;
        else
        {
            int j=0;
            while(prime[j]<=x&&j<num)
            {
                if(x%prime[j]==0)cnt[prime[j]]++;
                while(x%prime[j]==0)x/=prime[j];
                if(is_prime[x]){cnt[x]++;break;}
                j++;
            }
        }
    }
    for(int i=2; i<maxm; i++)
        cnt[i]+=cnt[i-1];
    scanf("%d",&m);
    while(m--)
    {
        int ans=0;
        scanf("%d%d",&l,&r);
        l=min(l,maxm-5);
        r=min(r,maxm-5);
        cout<<cnt[r]-cnt[l-1]<<endl;
    }
    return 0;
}

還有個方法，從小到大列舉數字，把他的倍數標記 

#include <stdio.h>
#include <string.h>

const int N = 10000001;

int vis[N], sum[N], v[N];

void init() {
	int num, n;
	scanf("%d", &n);
	for (int i = 0; i < n; i++) {
		scanf("%d", &num);
		vis[num]++;
	}
}

void cal() {
	for (int i = 2; i < N; i++) {
		if (v[i]) continue;
		for (int j = i; j < N; j += i) {
			if (vis[j]) sum[i] += vis[j];
			v[j] = 1;
		}
	}
}

void solve() {
	for (int i = 2; i < N; i++)
		sum[i] += sum[i - 1];
	int m, l, r;
	scanf("%d", &m);
	while (m--) {
		scanf("%d%d", &l, &r);
		if (r >= N) r = N - 1;
		if (l >= N) l = N;
		printf("%d\n", sum[r] - sum[l - 1]);
	}
}

int main() {
	init();
	cal();
	solve();
	return 0;
}


相關文章