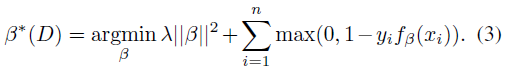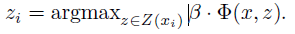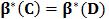（1）可變形部件模型

       可變形部件模型(DeformablePart Model)由三部分組成：

       (1) 一個較為粗糙的，覆蓋整個目標的全域性根模版(或叫做根濾波器)。

       (2) 幾個高解析度的部件模版(或叫做部件濾波器)。

       (3) 部件模版相對於根模版的空間位置。

 

       首先要計算一個HOG金字塔：通過計算標準影象金字塔中每層影象的HOG特徵得到HOG特徵金字塔，HOG金字塔中每一層的的最小單位是細胞單元(cell)。

       濾波器(模版)就是一個權重向量，一個w * h大小的濾波器F是一個含w * h * 9 * 4個權重的向量(9*4是一個HOG細胞單元的特徵向量的維數)。所謂濾波器的得分就是此權重向量與HOG金字塔中w * h大小子視窗的HOG特徵向量的點積(DotProduct)。

       而檢測視窗的得分是根濾波器的分數加上各個部件的分數的總和，每個部件的分數是此部件的各個空間位置得分的最大值，每個部件的空間位置得分是部件在該子視窗上濾波器的得分減去變形花費。

       假設H是HOG金字塔，p = (x, y, l) 表示金字塔第l層 (x, y) 位置的一個細胞單元。φ(H, p, w, h)是將金字塔H中以p為左上角點的w * h大小子視窗的HOG特徵串接起來得到的向量。所以，濾波器F在此檢測視窗上的得分為：F·φ(H, p, w, h)。此後，在不引起歧義的情況下，我們使用φ(H,p)代表φ(H, p, w, h)。

       所以，含n個部件的模型可以通過根濾波器F₀和一系列部件模型(P₁,..., P_n)來定義，其中Pi = (Fi, vi, si, ai, bi)。Fi是第i個部件的濾波器；vi和si都是二維向量，都以細胞單元為單位，vi指明第i個部件位置的矩形中心點相對於根位置的座標，si是此矩形的大小；ai和bi也都是二維向量，指明一個二次函式的引數，此二次函式用來對第i個部件的每個可能位置進行評分。

       模型在HOG金字塔中的位置可以用z = (p₀, ..... , p_n)來表示，當i=0時，p_i = (x_i, y_i,l_i )表示根濾波器的位置；i>0時，p_i = (x_i, y_i,l_i )表示第i個部件濾波器的位置。我們假設每個部件所在層的HOG細胞單元的尺寸是根所在的層的細胞單元尺寸的一半。空間位置的得分等於每個部件濾波器的得分(從資料來看)加上(？加上減去都一樣，通過正負號控制就行)每個部件的位置相對於根的得分(從空間來看)。

即：

(1)式中左邊表示所有濾波器(i從0開始，包括根濾波器和部件濾波器)的得分(即濾波器的權重向量與對應的HOG特徵向量的點積)，右邊表示所有部件濾波器(i從1開始)的形變花費。

其中：

表示部件i的變形程度， 和在-1到1之間。

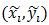
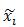
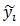
(x₀,y₀)是根濾波器在其所在層的座標，為了統一到部件濾波器所在層需乘以2。

vi是部件i相對於根的座標偏移，所以2(x0, y0)+vi表示未發生形變時部件i的座標，

所以(xi,yi) – [2(x0,y0) + vi]是部件i的形變位移量，再除以部件的矩形框大小si可保證在-1到1之間。

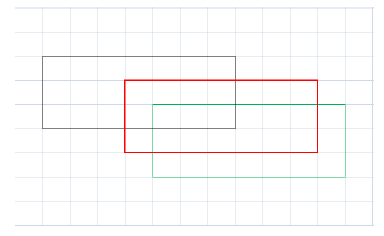
       計算過程如下圖：

圖中每個格子表示部件所在HOG金字塔層的細胞單元，紅框表示某部件未發生位移時的位置，w=7，h=3.黑框表示部件的實際位置，因此

同理，綠框所在位置對應：

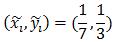
（2）在不完全標註(partially labeled)資料集上的學習

模型訓練使用的資料集中只標註了整個目標的位置，沒有標註出每個部件的位置，所以叫做部分標註或不完全標註，並不是說圖片中有指定類別的目標沒有標註出來，這裡容易理解錯誤。

這種訓練方法可以看做弱監督訓練，正因為不知道目標中部件的位置，所以將部件的位置看做隱藏變數，使用LSVM進行訓練，訓練時同時估計部件位置和學習模型引數。

（3）半凸

       LSVM最終是一個非凸規劃(non-convex)問題。然而，在下面所討論的情況下LSVM是半凸規劃(semi-convexity)問題，一旦將隱藏資訊指定給正樣本則訓練問題變為凸規劃問題。

       幾個凸函式的最大值問題是凸規劃問題。線上性SVM中，有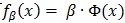是β的線性函式，此時鉸鏈損失函式對於每個樣本都是凸的，因為它是兩個凸函式的最大值。

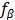
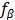
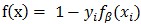
       注意到公式(13)中定義的是一系列函式的最大值，而這些函式都是β的線性函式，因此是β的凸函式。所以當yi = -1時，兩個函式f(x) = 0和都是β的凸函式，所以鉸鏈損失函式 是β的凸函式。也就是說，只有當樣本為負樣本時，損失函式是β的凸函式。我們將損失函式的這一性質叫做半凸(semi-convexity)。

       對於正樣本(yi= 1)來說，LSVM的鉸鏈損失函式不是凸函式，因為它是一個凸函式f(x)= 0 和一個凹函式 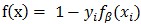 的最大值。

       但是，當LSVM的正樣本的隱藏變數具有唯一可能的取值時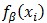， 是β的線性函式，因此損失函式是β的凸函式，再加上半凸性質，公式(14)變為凸規劃問題。

 

（4）座標下降演算法

       對於含有隱藏變數的svm問題，使用座標下降演算法進行求解：

       

        (1) 估計部件位置

保持β值不變，即將β看做常量，找到正樣本的隱藏變數z_i的最優值：

        (2) 學習模型引數

保持正樣本的z_i值不變，即將z_i看做常量，通過解上面定義的凸規劃問題(即標準SVM問題)最優化β值。

（5）難例挖掘定理

 定理1 設C是樣本集D的一個子集，如果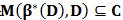 則

解釋：在樣本集D上訓練一個分類器β( 即β*(D))，用β在樣本集D上搜尋難例，得到難例集合即為M(β*(D), D)，如果此難例集合包含於樣本子集C，則在樣本子集C上訓練得到的分類器等價於在樣本集D上訓練得到的分類器。

 

定理2 

解釋：現在有分類器β，β在樣本集D上得到的難例集合為M(β,D)，用M(β,D)訓練一個分類器，即為β*(M(β, D))，如果訓練出來的分類器等於β (這說明什麼呢？這說明初始分類器β已經足夠好了，因為再加入難例進行訓練得到的是和初始分類器相同的分類器)，則β就是樣本集上的最優分類器。

迭代演算法：

       設C是最初的樣本緩衝區(cache)。實際上可以將正樣本和隨機負樣本放在一起。考慮如下迭代演算法：

       (1)設β:= β*(C)

       (2)收縮C，使得C := M(β,C)

       (3)通過不斷向C中增加M(β, D)中的樣本來增大C，直到達到記憶體限制L。

解釋：

       (1)C是一個樣本緩衝區，在C上訓練一個分類器β，即為β*(C)。

       (2)用β在C上搜尋得到的難例代替C，使C變小(收縮)。

       (3)用β在原樣本集D上搜尋難例，得到難例集M(β, D)，從M(β, D)中拿出樣本新增到C中，直到達到記憶體限制L。

       重複步驟(1)，在C上訓練一個新的分類器β，繼續重複步驟(2)(3)。就這樣不斷重複步驟(1)(2)(3)，不斷迭代。

 

定理3如果每次經上述演算法步驟2的迭代後，有|C|<L，則演算法在有限時間內會收斂到。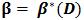

解釋：定理3是一個收斂條件，因為在定理2中迭代演算法的第(3)步裡會將樣本緩衝區C增加到L大小，如果進行下一次迭代時，C可以變小，就說明演算法在收斂。怎麼理解呢？將分類器看做是一個學生，此學生在學習新知識，不斷加入的新難例就是新知識，緩衝區C就是學生的書包，新加入的知識放到學生的書包中，如果每次學習過程書包變小，就說明學生將一些新加入的知識消化了，變成了學生的一部分。隨著學習過程的進行，新知識一點一點被消化，學生也變得越來越聰明。在這裡就是隨著迭代過程的進行，難例被一點一點消化，分類器逐漸變得更好。

A Discriminatively Trained, Multiscale,Deformable Part Model[CVPR 2008]的中文翻譯

Object Detection with Discriminatively Trained Part Based Models[PAMI 2010]的中文翻譯  

Deformable Part Model 相關網頁：http://www.cs.berkeley.edu/~rbg/latent/index.html

Pedro Felzenszwalb的個人主頁：http://cs.brown.edu/~pff/

PASCAL VOC 目標檢測挑戰：http://pascallin.ecs.soton.ac.uk/challenges/VOC/

有關可變形部件模型(Deformable Part Model)的一些說明