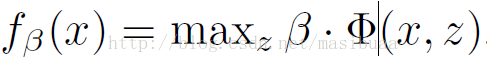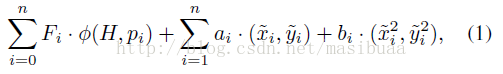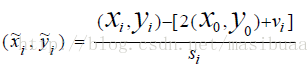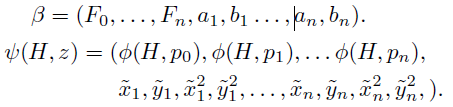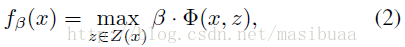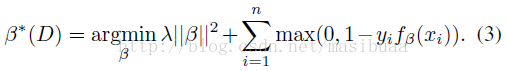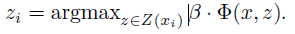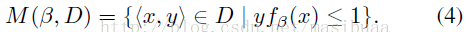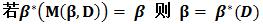判別訓練的多尺度可變形部件模型

Pedro.Felzenszwalb，David.McAllester，Deva.Ramanan

 

 

 

摘要

       本文介紹了一種用於目標檢測的判別訓練的多尺度可變形部件模型。我們的系統在平均精度上達到了2006 PASCAL 人體檢測競賽中最優結果的兩倍，同樣比2007 PASCAL目標檢測比賽中20個類別中的10個的最優結果都要好。此係統非常依賴於可變形部件模型。隨著可變形部件模型逐漸流行，它的價值並沒有在類似PASCAL的較難的資料集上被展示。我們的系統還依賴於判別訓練的新方法。我們將一種挖掘難例(Hard Negative Example)的間隔敏感方法與隱藏變數SVM(Latent variable SVM)結合在一起。隱藏SVM類似於隱藏條件隨機場(Hidden CRF)問題，最終是一個非凸規劃的訓練問題。隱藏SVM是半凸規劃(semi-convex)問題，但是一旦將隱藏資訊指明給正樣本，則訓練問題變為凸規劃問題。我們相信我們的訓練方法最終可以利用更多的隱藏資訊，例如層次(grammar)模型以及包含隱式三維姿態的模型。

      

1 引言

       我們所研究的是在靜態圖片中的某類目標(例如人、車)的檢測和定位問題。我們提出了一種多尺度可變形部件模型來解決此問題，此模型的判別訓練過程只需要正樣本的標註矩形框(意思是說只需要整個目標的標註資訊，不需要各個部件的標註資訊)。基於此模型實現了一個高效而精確的檢測系統，可以在兩秒內處理一張圖片並達到明顯比之前方法更高的檢測精度。

       我們的系統在平均精度上可以達到2006 PASCAL人體檢測挑戰賽最佳結果[5](Dalal的HOG方法)檢測精度的兩倍，同樣比2007 PASCAL目標檢測中20個類別中的10個的最優結果都要好。圖1顯示了我們的人體模型的檢測結果。

圖1 人體模型的檢測結果。此模型是由一個粗糙的全域性模版、幾個高解析度的部件模版和每個部件之間的空間模型構成的。

 

     目標可被可變形部件表示的概念提供了表示目標類別的框架[1-3,6,10,12,13,15,16,22]。儘管這些模型在概念上很吸引人，但是很難在實際中實現。在一些難度大的資料集上，可變形模型經常被一些從理論上看很弱的模型——例如剛體(固定rigid)模版[5]或特徵袋[23]——在實踐中所超越。我們的主要目標就是要解決這一問題。

       可變形部件模型包括一個粗糙的包含整個目標的全域性模版，以及若干個高解析度的部件模版，所謂的模版就是梯度方向直方圖HOG[5]特徵向量。就像[14,19,21]中所述，模型是判別訓練的。然而，我們的系統是半監督的，使用最大間隔框架進行訓練，並且不依賴於特徵檢測。我們還介紹了一種簡單而有效的從非完美標註的資料集中學習部件模型的方法。和論文[4]中的需要大量計算的方法不同，我們的方法在單CPU上可以在3小時內學習一個模型。

       此論文的另一個貢獻是提出了一種新的判別訓練方法，我們為處理隱藏變數例如部件位置擴充套件了SVM，並且提出了一種挖掘難例(HardNegative Examples)的新方法。我們認為處理部分標註的資料是機器學習在計算機視覺領域中的一個重要問題。例如，PASCAL的資料集只給出了每個目標的正樣本的矩形框。我們將目標的每個部件的位置看做隱藏變數，同時也將目標的位置看做是隱藏變數，只需要我們的分類器選出一個與已標註的矩形框有大量重疊的視窗。

       隱藏SVM就像條件隨機場CRF[19]一樣，最終是一個非凸訓練問題。然而，隱藏SVM是半凸規劃(semi-convex)問題，但是一旦將隱藏資訊指明給正樣本，則訓練問題變為凸規劃問題，可使用一般的座標下降演算法求解。

      

系統綜述

       我們的系統使用視窗掃描方法。目標模型包括一個全域性的根濾波器和幾個部件模型。每個部件模型包括一個空間模型和一個部件濾波器，空間模型定義了一系列此部件相對於檢測視窗的空間位置，以及每個相對位置的變形花費。

       檢測視窗的得分是根濾波器的分數加上各個部件的分數的總和，每個部件的分數是此部件的各個空間位置得分的最大值，每個部件的空間位置得分是部件在該子視窗上濾波器的得分減去變形花費。這與經典的基於部件的模型很相似[10][13]。根濾波器和部件濾波器的得分都是通過計算視窗內的梯度方向直方圖和一些權重的點積來獲得的。根濾波器就等價於Dalal-Triggs的HOG模型[5]。部件濾波器的特徵是在兩倍根濾波器解析度的空間上計算的。我們的模型是在混合尺度中定義的，檢測目標時通過搜尋影象金字塔來實現。

       訓練使用一系列含標註的影象，每個目標的例項都有一個矩形框。我們將檢測問題轉換為二分類問題。對於每個樣本x，通過下式計算x的得分：

β是模型的引數向量，z是隱藏變數(例如部件的位置)。我們定義了一種擴充套件的SVM，叫做隱藏變數SVM(LSVM,Latent variable SVM)。LSVM的一個重要特性是，當將隱藏資訊指明給正樣本時，則訓練問題變為凸優化問題，從而可以使用座標下降演算法求解。

       在實際中，我們對三元組(<x₁, z₁,y₁>, ... , <x_n, z_n, y_n>)迭代地應用經典SVM方法，其中z_i是上一次迭代學習到的模型中最適合x_i的隱藏標籤。最初的根濾波器由PASCAL資料集的矩形框所標定的目標產生，各個部件根據根濾波器進行初始化。

 

 

2 模型

       我們模型的潛在基礎是論文[5]中的方向梯度直方圖(HOG)。我們在兩個不同的尺度上提取HOG特徵：全域性固定模版使用粗糙特徵，可以覆蓋整個檢測視窗；區域性部件模版使用精細尺度特徵，可以相對於檢測視窗移動。部件相對位置的空間模型等價於星型圖或論文[3]中的1-fan圖，而粗糙全域性模版作為位置參考。

 

2.1HOG描述子

       我們根據論文[5]中的描述來構建HOG特徵。影象首先被劃分為不重疊的8*8畫素區域，或者叫做細胞單元(cell)。對於每個細胞單元統計一個一維的梯度方向直方圖，這些直方圖可以表示區域性形狀特徵，並且能適應小的形變。

       每個畫素的梯度方向被離散到9個方向bin之一，而每個畫素的梯度幅值為方向進行投票。對於彩色圖，分別計算每個通道的梯度，選取梯度幅值最大的那個通道的梯度作為畫素點的梯度。然後，將2*2個細胞單元組成塊(block)，對塊進行歸一化，形成一個9*4大小的向量。

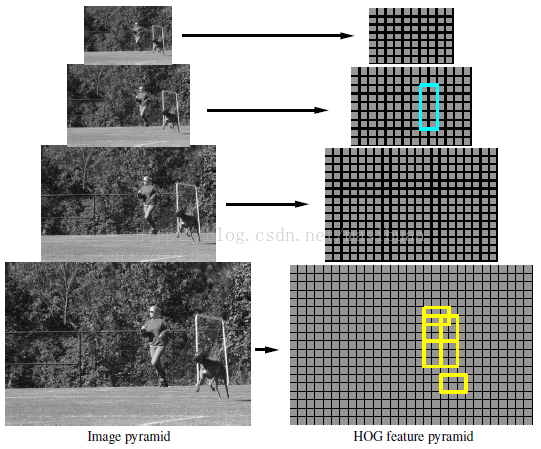
       通過計算標準影象金字塔中每層影象的HOG特徵，我們定義了一個HOG特徵金字塔，HOG金字塔中每一層的的最小單位是細胞單元，見圖2。金字塔頂層的特徵可以在大範圍內捕獲粗糙的梯度直方圖，金字塔底層的特徵捕獲小範圍的精細尺度梯度直方圖。

圖2，HOG特徵金字塔以及人的模型在該金字塔內的示例。藍色矩形表示根濾波器的作用區域，每個黃色矩形表示對應的部件濾波器的作用區域。部件濾波器被放置在兩倍空間解析度於根濾波器位置的層。

 

2.2濾波器(模版)

       濾波器就是指定HOG金字塔子視窗權重的矩形模版，一個w * h大小的濾波器F是一個含w * h * 9 * 4個權重的向量。所謂濾波器的得分就是此權重向量與HOG金字塔中w * h大小子視窗的HOG特徵向量的點積(Dot Product)。

       論文[5]中的系統使用單個濾波器來定義目標模型，通過對HOG金字塔中每個w * h大小子視窗的得分進行閾值化來檢測特定類別的目標。

       假設H是HOG金字塔，p = (x, y, l) 表示金字塔第l層 (x, y) 位置的一個細胞單元。

φ(H, p, w, h)是將金字塔H中以p為左上角點的w * h大小子視窗的HOG特徵串接起來得到的向量。所以，濾波器F在此檢測視窗上的得分為：F·φ(H, p, w, h)。此後，在不引起歧義的情況下，我們使用φ(H, p)代表φ(H, p, w, h)。

 

2.3可變部件模型

       我們的可變形部件模型包括一個覆蓋整個目標的粗糙的根濾波器(root filter)，和若干個表示目標各個部件的高解析度的部件濾波器(part filter)。圖2表明此模型在HOG金字塔中的位置。根濾波器的位置定義了檢測視窗(即濾波器中的細胞單元所包含的所有畫素)。部件濾波器位於金字塔的下幾層，使得部件濾波器所在層的HOG細胞單元尺寸是根濾波器所在層的細胞單元尺寸的一半。

       我們發現使用高解析度的特徵來定義部件濾波器對於獲得高識別率是必要的，這樣部件濾波器相比於根濾波器就可以表示更細膩的邊緣資訊。例如在建立人臉模型時，根濾波器用來捕獲臉的邊界這些粗糙資訊，部件濾波器可以捕獲眼鏡、鼻子、嘴這些細節資訊。

       含n個部件的模型可以通過根濾波器F₀和一系列部件模型(P₁, ..., P_n)來定義，其中

Pi =(Fi, vi, si, ai, bi)。Fi是第i個部件的濾波器；vi和si都是二維向量，都以細胞單元為單位，vi指明第i個部件位置的矩形中心點相對於根位置的座標，si是此矩形的大小；ai和bi也都是二維向量，指明一個二次函式的引數，此二次函式用來對第i個部件的每個可能位置進行評分。圖1展示了一個人體模型。

       模型在HOG金字塔中的位置可以用z =(p₀, ..... , p_n)來表示，當i=0時，p_i= (x_i, y_i, l_i )表示根濾波器的位置；i>0時，p_i= (x_i, y_i, l_i )表示第i個部件濾波器的位置。我們假設每個部件所在層的HOG細胞單元的尺寸是根所在的層的細胞單元尺寸的一半。空間位置的得分等於每個部件濾波器的得分(從資料來看)加上(？加上減去都一樣，通過正負號控制就行)每個部件的位置相對於根的得分(從空間來看)。

即：

注意：上式是原版論文中的公式，如果表示為減去變形花費就是：

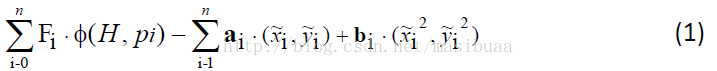
其中

    

注意：上式是原版論文中的，可能是寫錯了，否則解釋不通，正確的是：

(x₀,y₀)是根濾波器在其所在層的座標，為了統一到部件濾波器所在層需乘以2。

vi是部件i相對於根的座標偏移，所以2(x0, y0)+vi表示未發生形變時部件i的座標。

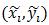
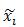
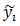
所以 表示部件i的變形程度， 和在-1到1之間。

       模型在HOG金字塔中的位置有很多可能(指數級)，我們使用動態規劃和距離變換方法[9][10]來計算模型中各個部件的最佳位置，使其成為根位置的函式。這會花費O(nk)的時間，n是模型中的部件個數，k是HOG金字塔中細胞單元的個數。在進行目標檢測時，根據各個部件的最可能位置來對根位置評分，然後對此分數進行閾值化。

       空間位置z的得分可以表示為模型引數向量β與向量ψ(H, z)的點積，即β·ψ(H, z)，其中：

ψ(H, z)可以簡單的理解為HOG金字塔H中模版z對應的特徵向量。

我們使用此表示式來學習模型引數，它將可變形部件模型和線性分類器聯絡了起來。

       這裡定義的空間模型的一個有意思的地方是我們允許引數(a_i, b_i)是負的，如此以來，相對於此前的quadratic”spring”？花費，此模型變得更具通用性。

 

 
3 學習

       PASCAL訓練資料集包含大量用矩形框標註目標例項的圖片。我們把利用這些資料學習可變形部件模型的問題簡化為二分類問題。設D = (<x₁, y₁>, ..., <x_n, y_n>)是標註好的一系列樣本，其中y_i∈{-1, 1}是樣本類別，H(x_i)是HOG金字塔，Z(x_i)是根濾波器和部件濾波器的合法位置。我們從訓練集的矩形框中擷取正樣本，對於這些樣本定義Z(xi)，其中根濾波器的位置必須至少和矩形框的位置重疊50%。負樣本來自不包含目標的圖片，圖中每個根濾波器的位置產生一個負樣本。

       注意在正樣本中，我們將根濾波器和部件濾波器的位置看做隱藏變數。我們發現在訓練時允許根濾波器的位置存在不確定性可以很大程度上提高系統的表現(見第四部分)。

 

3.1隱藏變數SVM

       隱藏變數SVM的定義如下。對每個輸入樣本x用以下函式進行評分：

其中β是模型引數向量，z是一系列隱藏變數。對於可變形模型，定義Φ(x, z) = ψ(H(x), z)，所以β·Φ(x, z)是根據位置z放置模型的得分。

       類比經典SVM，根據標註的樣本集D =(<x₁, y₁>, ..., <x_n, y_n>)，通過最優化下面的目標函式來訓練模型引數β，β*(D) 表示樣本集D上的最優β值(或者說是根據樣本集D訓練得到的模型引數β)：

如果將隱藏變數域Z(x_i)指明為確定的值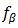， 變為確定的數β，由此就變為線性SVM問題，這是隱藏變數SVM的一個特例。隱藏變數SVM是通用的基於能量的模型(energy-based models)[18]的一個例項。

 

3.2半凸

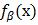
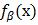
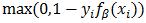
       公式(2)中定義的 是β的線性函式的最大值，因此是β的凸函式。這意味著，當y_i是-1時(即對於負樣本)，鉸鏈損失(hinge loss)是β的凸函式。也就是說，對於負樣本來說損失函式是β的凸函式，我們將損失函式的這一特性叫做半凸。

       如果LSVM中正樣本的隱藏變數域Z(x_i)指明為確定值，則每個正樣本的損失函式變為凸函式，加上損失函式的半凸性質，所以公式(3)是β的凸函式。

       如果正樣本的隱藏變數不確定，可以使用座標下降演算法計算公式(3)的區域性最優：

1) 保持β值不變，找到正樣本的隱藏變數z_i的最優值：

      

2) 保持正樣本的z_i值不變，通過解上面定義的凸規劃問題(標準SVM)最優化β值。

 

       可以看出以上兩個步驟或者優化目標函式(3)的值或者維持目標函式值不變。如果兩個步驟都使目標函式值保持不變的話(達到收斂)，就得到了目標函式(3)的較強的區域性最優值。步驟1在指數空間內搜尋正樣本的隱藏變數，同時步驟2搜尋權重向量和指數空間內負樣本的隱藏變數。

 

3.3難例資料探勘

       在目標檢測中，用於訓練的大多數樣本都是負樣本，因此不可能同時考慮所有的負樣本。所以，經常需要構建包含正樣本和負樣本難例(難樣本,Hard Negative,Hard Example,Hard Instance )的訓練集，其中的負樣本難例是從大範圍的可能負樣本中挖掘出來的。

       這裡我們介紹一種適用於SVM和LSVM的對樣本進行資料探勘的方法。此方法只用難例來迭代解決子問題。此方法的創新之處是能夠在理論上保證最終會得到完全訓練集之上的訓練問題的準確解。此方法需要用到難例的間隔敏感特性。

       這裡討論的結果既適用於經典SVM問題，又適用於LSVM的座標下降演算法中的步驟2所定義的問題。由於空間有限，這裡忽略證明過程。此方法與論文[17]中的工作集方法有關。

       模型引數β在樣本集D上的難例表示為：

即M(β,D)是分錯類的訓練樣本或靠近由β定義的分類器邊緣的樣本。接下來我們要說明樣本集D上的最優β值β*(D)只依賴於難例。

 

定理1 設C是樣本集D的一個子集，如果 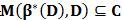 則

       這意味著，理論上我們可以使用一個更小的樣本集合進行訓練，此樣本集是根據最優模型β*(D)定義的。

       給定一個固定的β，可以用M(β,D)來近似M(β*(D), D)。如此一來，就可以使用一種迭代演算法，不斷地根據上次迭代產生的模型引數β定義的難例來計算模型引數β。

 

定理2 

       設C是最初的樣本緩衝區(cache)。實際上可以將正樣本和隨機負樣本放在一起。考慮如下迭代演算法：

       (1) 設β:= β*(C)

       (2) 收縮C，使得C := M(β,C)

       (3) 通過不斷向C中增加M(β, D)中的樣本來增大C，直到達到記憶體限制L。

 

定理3 如果每次經上述演算法步驟2的迭代後，有|C|<L，則演算法在有限時間內會收斂到 。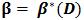

 

 

3.4實現細節

       我們討論的很多思想在系統中只得到了近似實現。事實上，在訓練LSVM時，是對三元組<x₁, z₁,y₁>, ... , <x_n, z_n, y_n>迭代應用經典SVM演算法。其中，z_i是上一次迭代中對x_i得分最高的隱藏標籤。每個三元組對應一個用來訓練線性分類器的樣本<Φ(x_i, z_i), y_i>。這使得我們可以使用一個經過優化的SVM工具包SVMLight[17]。在單個CPU上，每個PASCAL資料集中的目標類別大概需要3到4個小時的訓練時間，這其中包括部件的初始化時間。

       根濾波器初始化：對於每個目標類別，根據訓練資料集中目標矩形框大小的統計值，自動選擇根濾波器的尺寸。使用不含隱藏變數的SVM訓練得到一個初始的根濾波器F₀。正樣本從PASCAL資料集中含無遮擋的目標的圖片中擷取得到，這些擷取的正樣本非均勻地縮放到根濾波器大小的尺寸和長寬比。負樣本從不包含目標的圖片中隨機擷取。

       根濾波器更新：給定上一步訓練得到的初始根濾波器，對於訓練集中的每個矩形框，在根濾波器和矩形框顯著重疊(重疊50%以上)的條件下，找到濾波器得分最高的一個位置。此過程是在原始的、未縮放的圖片上進行的。用得到的新的正樣本集和初始的隨機負樣本集重新訓練F₀，如此迭代兩次。

       部件濾波器初始化：我們使用一種簡單的啟發式方法根據上面訓練的根濾波器初始化六個部件濾波器。首先選擇面積a，使得6a等於根濾波器面積的80%。使用貪心方法從根濾波器中選出面積為a的具有最大正能量(most positive energy，正能量是該區域中所有細胞單元的正權重平方和)的矩形區域，將此區域的所有權重清零然後繼續選擇，直到選出六個矩形區域。部件濾波器的初值是對應矩形區域內根濾波器的權值，但需要進行插值來適應更高的空間解析度。每個位置的初始變形花費是位移的平方，引數是a_i = (0,0)，b_i = -(1,1)。

       模型更新：通過構建新的訓練資料三元組來更新模型。對於訓練資料集中每個正樣本矩形框，在保證至少50%重疊的情況下用現有檢測器在所有可能位置和尺度進行檢測，在其中選出具有最高得分的位置作為此矩形框對應的正樣本(如圖3)，放入樣本緩衝區中。在不包含目標物體的圖片中選擇檢測得分高的位置作為負樣本，不斷向樣本緩衝區中新增負樣本直到檔案最大限制。利用SVMLight在緩衝區中的正負樣本上訓練新的模型，所有樣本都有部件位置標註。使用上一節中描述的樣本緩衝區策略迭代更新模型10次。在每次迭代過程中，將上一次樣本緩衝區的難例儲存下來，並不斷向緩衝區中新增新的難例。最後一次迭代完成後，緩衝區中保留下來所有的樣本難例M(β,D)，並且所有模型引數也已通過訓練獲得。

圖3，左邊的圖顯示了人體正樣本的所有隱藏變數的最優位置。虛線矩形框是PASCAL訓練集提供的目標的標註矩形框。大的實線矩形框是檢測視窗的位置，小的實線矩形框是各個部件的位置。右邊的圖顯示的是一個難例(Hard Negative Example)。

 

 
4 結果

       我們在PASCAL VOC 2006和2007挑戰賽上測試了我們的系統。論文[7][8]中有詳細的結果描述，需要強調的是，PASCAL VOC被公認為是非常難的目標檢測實驗資料集。資料集中包含幾千個真實世界場景的圖片，在其中標註了幾個類別的ground-truth矩形框，只有當檢測結果的矩形框和ground-truth矩形框重疊超過50%時才被認為是檢測正確。通過一條精度-召回率曲線(precision-recall curve)的平均精度(AP Average Precision)對系統進行評價(精度：檢測正確的目標占檢測的總目標的比例。召回率：檢測到的目標占ground-truth中標註的所有目標的比例)。

       近來在行人檢測領域趨向於用檢測率-每視窗誤報率(False Positives Per Window)進行評價，通過剪裁後的正樣本和不包含目標的圖片進行測量。這種評價方法依賴於掃描視窗的解析度，忽略了非極大值抑制的影響，所以不適合比較不同的系統。我們認為PASCAL評價標準能夠更加可靠地對系統效能進行評價。

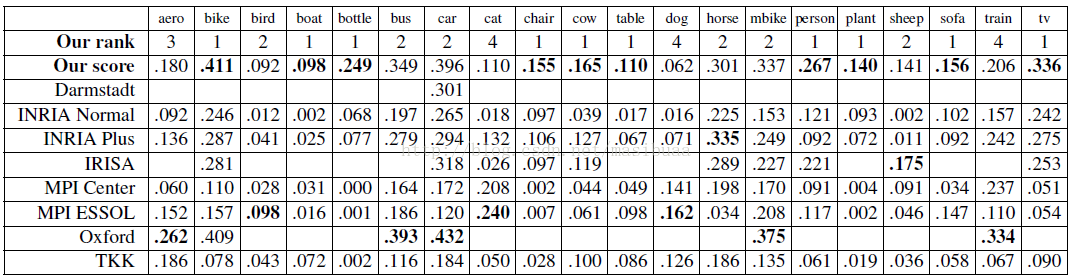
       PASCAL VOC 2007挑戰賽有20個目標類別。我們用系統的初始版本參加了官方的比賽，在6個類別上獲得了最高得分。我們當前的系統可以在10個類別上獲得最高得分，並在6個類別中獲得第二高得分。表1顯示了PASCAL 2007的比賽結果。

 

表1，PASCAL VOC2007比賽結果。表中顯示了我們的系統和參加比賽的其他系統的平均精度[7]。空白格表示該方法在對應的類別中沒有進行測試。每個類別的最高得分做了加粗處理。我們的當前系統可以在20個類別中的10箇中得到最高分，我們系統的初始版本可以在官方競賽的6個類別中得到最高分。

 

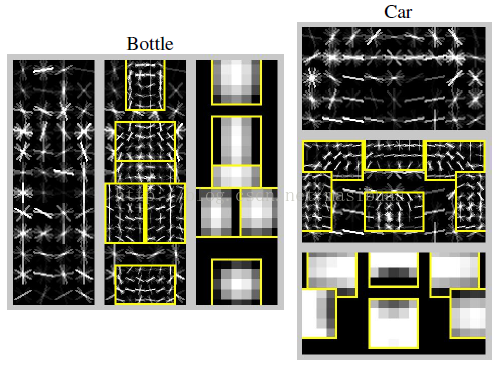
       我們的系統在剛體目標(例如車和沙發)和容易發生形變的目標(例如人和馬)上表現較好。同時還注意到，我們的系統在大量或少量訓練樣本的情況下都能成功。在人體類別中有大約4700個正訓練樣本，但在沙發類別中只有250個正訓練樣本。圖4是我們的系統學習到的一些模型。圖5展示了一些檢測結果。

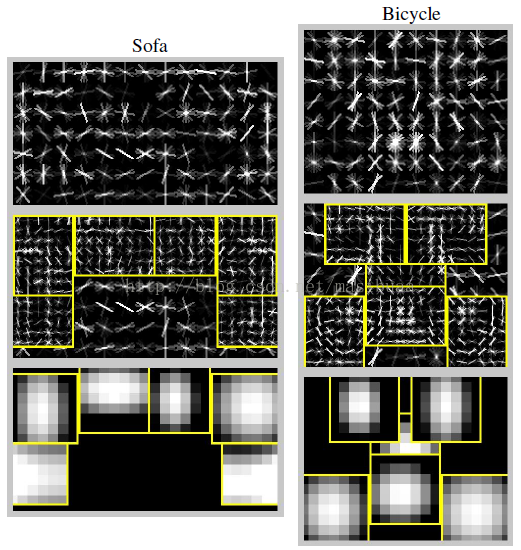
圖4，從PSACAL VOC 2007資料集中學習到的一些模型。圖中展示了根濾波器和部件濾波器中HOG細胞單元內所有方向的總能量，部件濾波器放置在所有允許位置的中心。圖中還顯示了每個部件的空間模型，亮的區域代表“代價低”的位置(即相對正確的部件位置)，黑的區域代表“代價高”的位置(即相對錯誤的部件位置)。

 

圖5，PASCAL 2007 資料集上的一些檢測結果。每行是同一個類別的模型的檢測結果(人，瓶子，小橋車，沙發，自行車，馬)。每行的前三列是正確的檢測結果，最後一列是誤報。圖中表明我們的系統可以檢測各種尺度(見小轎車的檢測結果)和各種姿勢(見馬的檢測結果)的目標。同樣可以檢測部分遮擋的目標，例如灌木叢後的人。就連誤報也經常是相當合理的，例如使用小轎車模型檢測出公共汽車，使用自行車模型檢測出自行車標誌，使用馬模型檢測出狗。通常情況下，每個部件濾波器都代表一個定位準確的有意義的目標部分，例如人體模型的頭部。

 

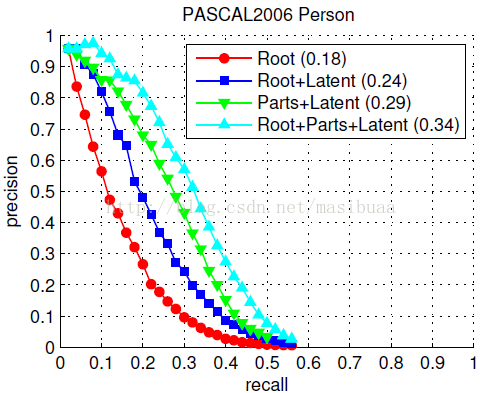
       我們在花費更長時間建立的2006人體資料集上評價系統的不同部分。PASCAL 2006人體檢測的最高AP得分是.16，是通過使用HOG特徵的固定模版獲得的[5]。之前得分.19的最好結果增加了一個基於分割的驗證過程[20]。圖6總結了我們訓練的幾個模型的效能。只含有根濾波器的模型等價於論文[5]中的模型，並且得到稍微高一點的.18AP。如果在模型中為每個正樣本增加隱藏的位置和尺度變數，使用LSVM進行訓練的話，效能會大幅增加到.24AP。這表明LSVM即使對於固定模版模型也是非常有用的，因為增加隱藏變數可以允許訓練資料中的檢測視窗進行自我調整。加入可形變部件模型後，效能增加到.34AP——之前最優結果的兩倍。最後，我們訓練了一個只含有部件濾波器沒有根濾波器的模型，可以達到.29AP，這說明了使用多尺度表示的優點。

圖6，系統在PASCAL VOC 2006人體資料集上的表現。Root代表只使用根濾波器並且沒有正樣本中檢測視窗的隱藏位置變數。Root +Latent表示使用帶有隱藏的檢測視窗位置變數的根濾波器。Parts + Latent表示帶有隱藏位置變數的部件濾波器，不含根濾波器。Root + Parts + Latent表示帶有檢測視窗隱藏位置變數的根濾波器和部件濾波器。

 

       我們還在PASCAL 2006人體資料集上考察了空間模型和允許形變數對系統效能的影響。如2.3節所述，si是部件的允許位移量(？si不是部件矩形框的大小嗎？)，以HOG細胞單元為單位。我們訓練一個固定的帶有高解析度部件的模型，將si設為0，此模型比只有根濾波器的模型要好，得分在.27AP到.24AP之間。在不使用形變花費的情況下，增加允許位移量，則結果會逐漸接近特徵袋方法(bag-of-features)。當si等於1時，效能達到最優，這表明約束部件的位移量很有必要。最優策略是：允許更大的位移量，同時加入形變花費(deformationcost)。下面的表格中的前三列是允許任意位移量的情況下系統的效能得分，最後一列是使用二次形變花費並最大允許位移量為2個HOG細胞單元的情況下系統的效能得分。

 

5 討論

       本文中介紹了一個訓練含有隱藏變數的SVM的通用框架。我們使用LSVM基於多尺度、可變形模型建立了一個識別系統。在不同測試集上的實驗結果表明我們的系統是目標檢測領域的當前最優結果(state-of-art)。

       LSVM可以探索目標識別中額外的隱藏結構。我們可以考慮更深的部件層次(部件中包含部件)，混合模型(汽車的前視模型和側視模型)，以及三維姿態。通過使用共享的部件詞典(shared vocabulary of parts)，我們可以訓練並同時檢測多個類別。我們還計劃使用A*搜尋[11]在檢測時高效的搜尋隱藏引數。

 

文章下載：http://download.csdn.net/detail/masikkk/6763781

Deformable Part Model 相關網頁：http://www.cs.berkeley.edu/~rbg/latent/index.html

Pedro Felzenszwalb的個人主頁：http://cs.brown.edu/~pff/

PASCAL VOC 目標檢測挑戰：http://pascallin.ecs.soton.ac.uk/challenges/VOC/

以及Pedro Felzenszwalb 在PAMI 2010的一篇更詳盡的期刊文章的翻譯：

Object Detection with Discriminatively Trained Part Based Models[PAMI 2010]的中文翻譯 

有關可變形部件模型(Deformable Part Model)中一些難點的一些說明：

http://blog.csdn.net/masibuaa/article/details/17534151