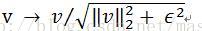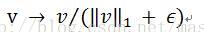用於人體檢測的方向梯度直方圖

Navneet Dalal，Bill Triggs

 

 

摘要

       我們研究了視覺目標檢測的特徵集問題，並用線性SVM方法進行人體檢測來測試，通過與當前的基於邊緣和梯度的描述子進行實驗對比，得出方向梯度直方圖(Histograms of Oriented Gradient,HOG)描述子在行人檢測方面表現更加突出。我們研究了計算過程中每一階段的影響，得出小尺度梯度(fine-scale gradients)、精細方向取樣(fine orientation binning)、粗糙空域抽樣(coarse spatial binning)以及重疊描述子塊的區域性對比度歸一化(local contrastnormalization in overlapping descriptor blocks)都對最終結果有重要作用。這種方法在最初的MIT行人資料庫上表現近乎完美，所以我們引入了一個更具挑戰性的包含1800個不同姿勢和背景的已標註人體資料集。

 

1 引言

       由於人體姿勢和外表的多變，在影象中檢測人體是一項具有挑戰性的工作。首先需要的就是一個強壯的特徵集，使得在不同光照和背景下都能清晰地分辨出人體。我們研究了人體檢測的特徵集問題，區域性歸一化的HOG描述子相比於現存的特徵集(包括小波[17,22])有更好的表現。相比於邊緣方向直方圖(EdgeOrientation Histograms[4,5])、SIFT([12])、形狀上下文(Shape Contexts[1])，HOG是在網格密集的大小統一的細胞單元(dense grid of uniformlyspaced cells)上進行計算，而且為了提高效能，還採用了重疊的區域性對比度歸一化(overlapping local contrastnormalizations)。我們用行人檢測(人體是大部分可見的並且基本上是直立的)進行測試，為了保證速度和簡潔性，使用線性SVM作為分類器。HOG檢測器在MIT的行人資料集([17,18])上表現相當好，所以我們又引入了一個更具挑戰性的包含1800個不同姿勢和背景的已標註人體資料集。正在進行的工作表明，我們的特徵集對於其他基於形狀的目標檢測也同樣好。

       第2節中簡要介紹了在人體檢測上前人的研究工作，第3節是HOG方法的總體介紹，第4節介紹了我們使用的資料集，第5-6節是HOG方法的詳細介紹以及不同處理階段的實驗結果，第7節是結論和總結。

 

2 前人的研究工作

       在目標檢測方向上有大量的文獻，這裡只列舉與人體檢測有關的論文[18,17,22,16,20]。[6]是一篇綜述。Papageorgiou等[18]提出了一種使用糾正哈爾小波(rectified Haarwavelet)作為特徵的多項式SVM行人檢測方法，以及[17]中基於子視窗的改進方法。Depoortere等給出了論文[2]中方法的一個最優化版本。Gavrila和Philomen[8]採用一種更直接的方法，提取邊緣圖並將其與樣本進行匹配，使用chamfer距離作為評判標準，這種方法已被用在一個實時行人檢測系統中[7]。Viola等[22]提出了一種高效的運動人體檢測器，使用AdaBoost來訓練一串漸進複雜的基於類Haar小波和時空差的區域拒絕規則。Ronfard等[19]提出了一種關節式的身體檢測器，他通過將基於SVM的肢體分類器合併到動態規劃框架中的一階和二階高斯濾波來實現，與Felzenszwalb和Huttenlocher[3]，以及Ioffe和Forsyth[9]的方法相似。

Mikolajczyk等[16]提出了一種方向位置直方圖和二值梯度幅值相結合的身體部位檢測器，能夠檢測臉、頭、以及身體上部或下部的前視或側視輪廓。相比之下，我們的檢測器結構更簡單，使用單一檢測視窗，但行人檢測的效果更好。

 

3 演算法概述

       此節是HOG特徵提取方法的概述，實現細節在第6節。此方法基於對稠密網格中歸一化的區域性方向梯度直方圖的計算。相似的特徵在過去十年中越來越多的被使用[4,5,12,15]。此類方法的基本觀點是：區域性目標的外表和形狀可以被區域性梯度或邊緣方向的分佈很好的描述，即使我們不知道對應的梯度和邊緣的位置。在實際操作中，將影象分為小的細胞單元(cells)，每個細胞單元計算一個梯度方向(或邊緣方向)直方圖。為了對光照和陰影有更好的不變性，需要對直方圖進行對比度歸一化，可以通過將細胞單元組成更大的塊(blocks)並歸一化塊內的所有細胞單元來實現。我們將歸一化的塊描述符叫做HOG描述子。將檢測視窗中的所有塊的HOG描述子組合起來就形成了最終的特徵向量，然後使用SVM分類器進行人體檢測，見圖1。

圖1

      

       圖1描述了我們的特徵提取和目標檢測流程。檢測視窗劃分為重疊的塊，在塊中計算HOG描述子，形成的特徵向量放到線性SVM中進行目標/非目標的分類。檢測視窗在整個影象的所有位置和尺度上進行掃描，並在輸出的用來檢測目標的金字塔上進行非極大值抑制，本文主要講特徵提取的過程。

       方向直方圖的使用已有很多先例[13,4,5]，但是直到Lowe的SIFT尺度不變特徵點提取[12]，才算達到成熟。SIFT型別的方法在[12,14]的程式中表現相當出色。形狀上下文[1]方法研究單元和塊的形狀，最初只使用邊緣畫素個數而不是方向直方圖，就已經獲得不錯的結果。這些稀疏特徵的成功，不禁使得作為稠密特徵的HOG方法的效果和簡易性黯然失色，我們希望我們的研究可以改變這一情況。特別地，我們的非正式實驗表明，即使現在最好的基於特徵點的方法，在人體檢測方面比我們方法的錯檢率也要高上至少1-2個數量級，主要是因為這些基於特徵點的檢測器不能可靠地檢測人體結構。

       HOG和SIFT特徵有個優點，它們提取的邊緣和梯度特徵能很好的抓住區域性形狀的特點，並且由於是在區域性進行提取，所以對幾何和光學變化都有很好的不變性：變換或旋轉對於足夠小的區域影響很小。對於人體檢測，在粗糙的空域取樣(coarse spatial sampling)、精細的方向取樣(fine orientationsampling)和較強的區域性光學歸一化(stronglocal photometric normalization)這些條件下，只要行人大體上能夠保持直立的姿勢，就容許有一些細微的肢體動作，這些細微的動作可以被忽略而不影響檢測效果。

 

 

4 資料集和研究方法

       資料集

       我們在兩個不同的資料集上進行了測試，第一個是MIT的行人資料庫[18]，包含城市場景中的509個訓練圖和200個測試圖(加上這些圖片的左右翻轉圖)，此資料集只包含正面和背面兩種視角，並且人體的動作有限。我們的檢測器在此資料集上表現近乎完美，所以我們製作了一個新的更具挑戰性的資料集，“INRIA”，包含從各種人體照片中剪下得到1805個64*128的行人圖片。這些人體大多數是站立的，但朝向各異並且背景多變，有些背景中還有人群。

       研究方法

       我們選擇了1239個行人圖片以及他們的左右翻轉圖作為訓練的正樣本，所以總共2478個正樣本。從1218個沒有行人的圖片中隨機擷取12180個檢測視窗大小的子圖作為初始的負樣本。用正負樣本訓練一個初始的分類器，然後用初始分類器在負樣本原圖上進行行人檢測，檢測出來的矩形區域自然都是分類錯誤的負樣本，這就是所謂的難例(hard examples）。然後，把誤報的負樣本(難例)集加入到初始的負樣本集中，重新訓練，生成最終的分類器，最終的SVM分類器檔案大約1.7GB。這種二次訓練的處理過程顯著提高了每個檢測器的表現(在我們的預設檢測器中使每個視窗的誤報率(FPPW False Positives Per Window)下降了5%)。

       為了量化檢測器的效能，我們提出了一個在雙對數座標上的評價曲線Detection ErrorTradeoff(DET)，即縱座標是漏檢率(miss rate，可以是1-recall rate(查全率、命中率)或者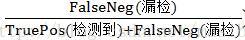)，橫座標是每個視窗的誤報率FPPW，兩個值都是越低越好。這種評價方法對於微小的概率變化都能檢測到，我們經常使用在10^-4FPPW時的漏檢率作為結果效能的參考點。DET曲線比較易變，稍微降低漏檢率就等價於在漏檢率不變時大幅增加誤報率FPPW。例如，對於我們的預設檢測器在FPPW為10^-4時，降低漏檢率1%相當於在漏檢率不變時以1.57倍的因子減少？FPPW。

 

5 結果綜述

       我們在此節比較HOG檢測器與已存在的一些方法的總體表現。我們的HOG檢測器基於矩形塊(R-HOG)或環形極座標塊(C-HOG)以及線性或核函式SVM，與Haar小波、PCA-SIFT或形狀上下文方法進行對比，這些方法的簡要介紹如下：

       廣義Haar小波

       這種方法是定向類Haar小波(oriented Haar-like wavelets)的擴充套件，與論文[17]中使用的方法類似(更優於)。這種特徵是從9*9和12*12定向一階和二階45度微分濾波器以及對應的二階微分xy濾波器改進得來。

       PCA-SIFT

       此描述子基於用PCA演算法將梯度圖投影到從訓練圖片中獲得的基底上[11]。Ke和Sukthankar表明此描述子在基於特徵點的影象匹配上要優於SIFT，但此說法有爭議[14]。我們對此演算法的實現使用16*16的塊，以及和我們的HOG描述子同樣的設定，PCA投影基底從正樣本圖片計算得到。

       形狀上下文ShapeContexts

       最初的形狀上下文[1]使用二值邊緣投票在極座標中統計bin，與邊緣方向無關。我們用1個方向bin的HOG描述子模擬了這一方法。使用內徑2個畫素，外徑8個畫素的16個角向和3個徑向間隔獲得最好結果。我們測試了基於梯度和邊緣投票的方法，邊緣閾值進行自動選擇來最優化檢測結果。

       結果

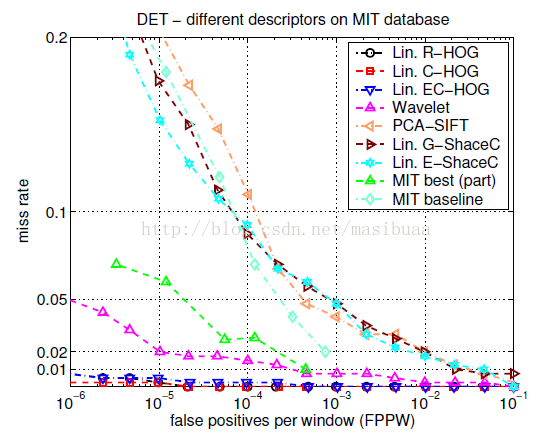
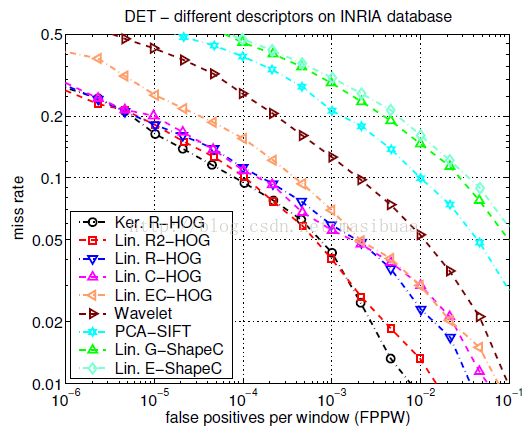
       圖3是不同的檢測器在MIT和INRIA測試集上的實驗結果。

圖3(a)

圖3(b)

 

       結果表明，HOG檢測器要顯著優於小波、PCA-SIFT、形狀上下文方法，在MIT資料集上相比於其他方法有非常明顯效能提升，在INRIA資料集上FPPW值有至少一個數量級的下降。我們的類Haar小波檢測器比MIT的小波檢測器效果好，因為我們使用了2階微分並對輸出向量進行了對比度歸一化。圖3(a)同樣顯示了MIT的最優方法及其整合的檢測器的結果(從[17]的實驗結果中插值計算得來)，然而由於我們不知道[17]中的資料集如何劃分為訓練集和測試集，所以無法進行精確的對比。矩形塊(R-HOG)和環形塊(C-HOG)檢測器表現相似，C-HOG有輕微的邊緣資訊。原始條形(定向2階微分)擴充套件R-HOG檢測器的特徵維數增加了一倍，同時效能也有較大提升(在10^-4FPPW時降低2%的漏檢率)。如果將線性SVM替換為高斯核函式SVM，在10^-4FPPW時有大約3%的效能提升，但以更高的執行時間為代價。以二值邊緣投票(EC-HOG)代替梯度幅值權重投票(C-HOG)會在10^-4FPPW時降低大約5%的效能，如果忽略方向資訊效能下降會更多，即使增加更多的空間或徑向bin也不管用。PCA-SIFT的表現很差勁，原因之一是，相比於[11]，為了保留住同樣的變化資訊，需要更多的主向量，這可能是由於沒有特徵點檢測器後空間配準能力變得更弱了。

 

6 演算法實現和效能研究

       在次節中我們會給出HOG演算法的詳細實現，並系統地分析不同的引數對效能的影響。檢測器引數如下：無伽馬校正的RGB顏色空間；梯度運算元為[-1,0,1]並且無平滑；梯度方向離散化(投票)到0-180間的9個bin中；塊(block)大小為16*16，細胞單元(cell)大小為8*8；高斯濾波引數σ為8；L2-Hys塊歸一化；塊移動步長為8個畫素；檢測視窗為64*128；線性SVM分類器。

       圖4總結了不同的HOG引數對總體檢測效果的影響，這些接下來我們會詳細討論，得出的結論是：要想檢測器效能好，需要精細尺度的微分(不需要平滑)，梯度方向直方圖的bin儘量多，尺寸適度的、歸一化的、重疊的描述子塊。

      

6.1 伽馬/顏色規範化

       我們用不同的冪值(gamma引數)評價了幾種顏色空間，有灰度空間、RGB、LAB，結果表明，這些規範化對結果影響很小，可能是由於隨後的描述子歸一化能達到相似的效果。如果顏色資訊可用，我們的特徵提取會使用顏色資訊，RGB和LAB顏色空間的結果相似，但如果使用灰度空間，在10^-4FPPW時有1.5%的效能下降。對每個顏色通道進行平方根gamma壓縮(即gamma引數為1/2)，會在10^-4FPPW時有1%的效能提升；如果將gamma引數改為對數，則會造成2%的效能下降。

 

6.2 梯度計算

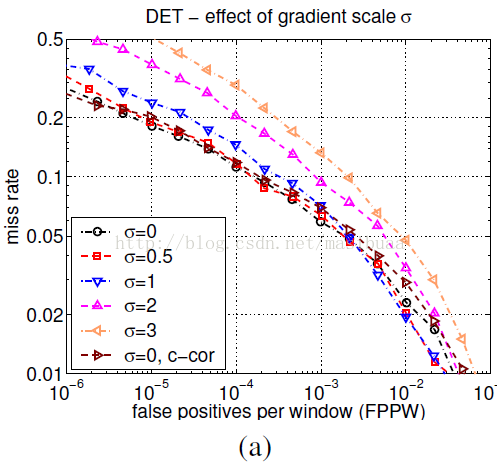
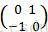
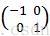
       不同的梯度計算方法對檢測器效能有很大影響，但事實證明最簡單的梯度運算元結果是最好的。我們先進行高斯平滑，然後應用幾種離散的微分模版來計算梯度。我們測試了不同平滑尺度(包括σ=0即不平滑)的高斯平滑，也測試了不同的梯度模版，包括一維模版([-1,1]、[-1,0,1]、[1,-8,0,8,-1])，3*3的Sobel模版，以及2*2的對角線模版和(最緊湊的中心二維微分模版)。簡單的[-1,0,1]模版在σ=0時表現最好。使用更大的模版往往會降低效能，而且增加高斯平滑也會降低效能：當平滑尺度σ從0變為2時，10^-4FPPW下的查全率(recallrate)從89%下降到80%，如圖4(a)。在σ=0時，5個因子的一維模版[1,-8,0,8,-1]比[-1,0,1]模版在10^-4FPPW下有1%的效能下降，2*2的對角線模版有1.5%的效能下降，無中心的[-1,1]模版也會導致1.5%的效能下降，推測是由於x和y方向上差分中心的不一致導致方向估計不準確。

       對於帶顏色的影象，分別計算每個顏色通道的梯度，以範數最大者作為該點的梯度向量。

圖4(a)

 

6.3 空間/方向bin統計

       計算細胞單元(cell)內每個畫素的梯度，為某個基於方向的bin投票(vote)，從而形成方向梯度直方圖。細胞單元可以是矩形的或者環形(極座標中的扇形)的。直方圖的方向bin在0度-180度(無符號梯度)或者0度-360度(有符號梯度)之間均分。為了減少混疊現象，梯度投票在相鄰bin的中心之間需要進行方向和位置上的雙線性插值。投票的權重根據梯度幅值進行計算，可以取幅值本身、幅值的平方或者幅值的平方根。實踐表明，使用梯度本身作為投票權重效果最好。

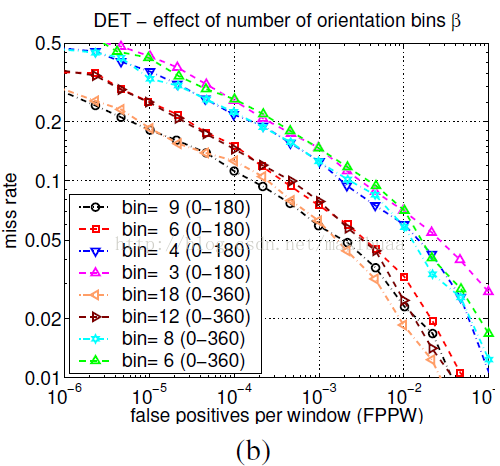
       精細的方向編碼對取得好的結果至關重要，然而空間取樣可以做的相當粗糙。如圖4(b)所示，增加方向bin的個數可以顯著提高檢測器的效能，直到大約9個bin為止，這裡所用的是無符號梯度的0度-180度均分方向直方圖。如果包括梯度符號資訊(方向範圍為0度-360度，類似SIFT描述子中使用的方向直方圖)會導致效能下降，即使bin的個數加倍來儲存原始方向資訊也不行。對於人體檢測來說，衣服和背景顏色的多變可能使得梯度符號資訊無意義，但對於其他目標檢測，例如汽車、摩托車，梯度符號資訊是有用的。

圖4(b)

 

6.4 歸一化和描述子塊

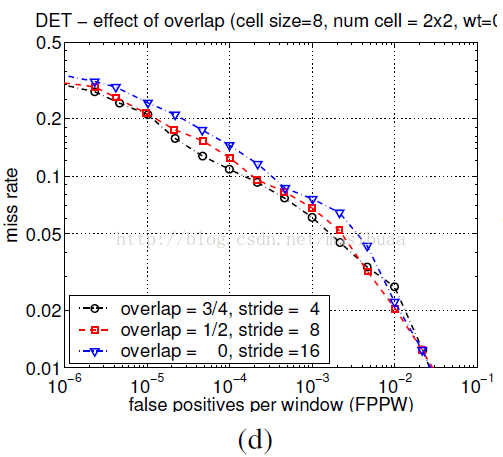
       由於區域性光照的變化，以及前景背景對比度的變化，使得梯度強度的變化範圍非常大，這就需要對梯度做區域性對比度歸一化。我們測試了多種不同的歸一化策略，大多數都是將細胞單元組成更大的空間塊(block)，然後針對每個塊進行對比度歸一化。最終的描述子是檢測視窗內所有塊內的細胞單元的直方圖構成的向量。事實上，塊之間是有重疊的，也就是說，每個細胞單元的直方圖都會被多次用於最終的描述子的計算。此方法看起來有冗餘，但可以顯著的提升效能。圖4(d)顯示了將重疊區域從0增加到重疊3/4塊時，10^-4FPPW下有4%的效能提升。

圖4(d)

 

       我們測試了兩種幾何形狀的塊，一種是矩形的塊，稱為R-HOG；一種是極座標中的環形塊，稱為C-HOG。

       R-HOG

       R-HOG塊與SIFT[12]描述子中使用的塊很相似，但用法不同。R-HOG塊描述子在單一尺度的稠密網格空間中進行計算，無主方向，並且作為更大的檢測視窗描述子的一部分被使用，檢測視窗描述子中明確含有塊之間的相對位置資訊。而SIFT特徵點描述子在多尺度空間下計算，具有尺度不變性，並需要旋轉到其主方向上，而且SIFT描述子是獨立使用的。SIFT描述子適合稀疏、寬基線的匹配，R-HOG描述子適合表示稠密空間的編碼。其他的先例包括Freeman和Roth[4]的邊緣方向直方圖。R-HOG塊可以用三個參數列示：ζ,η,β，塊大小為ζ*ζ，細胞單元大小為η*η，每個細胞單元有β個方向bin。

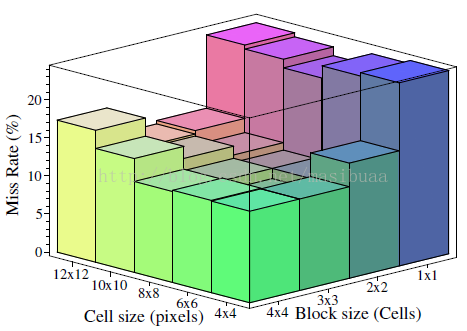
       圖5顯示了在10^-4FPPW時漏檢率隨不同的細胞單元和塊尺寸的變化情況。對於人體檢測，每個塊內含3*3個細胞單元，每個細胞單元含6*6個畫素時最優，此時漏檢率大約為10.4%。事實上，無論塊尺寸為多大，細胞單元為6-8個畫素寬時效能最優——巧合的是，我們的測試圖片中人體大約也是6-8個畫素寬。每個塊內含2*2或3*3個細胞單元時最優。除此之外，結果不好：當塊過大時，對區域性影象的適應性變差；當塊過小時，有價值的空間資訊減少。

圖5，10^-4FPPW時漏檢率隨細胞單元和塊尺寸的變化情況。塊步長(塊重疊區域)固定在塊尺寸的一半(即重疊區域為1/2)，細胞單元為6*6個畫素，每個塊內含3*3個細胞單元時效能最優，漏檢率大約為10.4%

 

       就像SIFT論文[12]中描述的，在統計直方圖bin之前用高斯加權使得塊邊緣的畫素的權重降低是有很用的。經試驗，在10^-4FPPW時使用σ =  0.5 *block_width的二維高斯核進行加權可使效能提升1%左右。

       我們還測試了在描述子中使用不同的細胞單元尺寸和不同的塊尺寸，效能有稍微的提高(在10^-4FPPW時提高3%)，但同時會大幅增加描述子尺寸。

       此外，我們還測試了垂直塊(含2*1個細胞單元)、水平塊(含1*2個細胞單元)以及既有垂直塊又有水平塊的描述子。垂直塊和垂直+水平塊明顯比只有水平塊要好，但還是不如2*2的方形塊好。

       C-HOG

       我們的環形塊描述子與形狀上下文[1]類似，只不過，每個細胞單元包含一個以梯度為權重的方向棧，而不是單純的方向無關的邊緣計數。極座標網格的想法源於允許精細的相鄰結構編碼與粗糙的廣域上下文編碼相結合的思想，以及訊號由視覺向人類大腦皮層的轉換是對數級的這一事實[21]。實時證明，含有很少的半徑bin的描述子結果最好，所以實際中幾乎不會有不均勻的情況出現。可以將C-HOG簡單看做中心環繞編碼的一種高階形式。

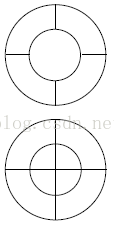
       C-HOG的塊有兩種形式，一種是中間有一個完整細胞單元的形式(類似[14]中的GLOH特徵)，另一種是中心單元被分為四個90度扇形的形式，類似形狀上下文方法，如下圖所示。

我們只提供中心有完整細胞單元的C-HOG的結果，相比於中心被分割的C-HOG，這種方法有更少的空間劃分，但實際效果卻是相同的。C-HOG可以用四個參數列示：角度bin的個數，半徑bin的個數，中心圓的半徑(以畫素為單位)，子半徑的伸展因子。要想保證好的效能，至少需要兩個半徑bin(一箇中心半徑、一個周圍的半徑)，四個角度bin。增加額外的半徑bin並不能改善多少效能，如果增加角度bin的個數反而會降低效能(從4個增加到12個會在10^-4FPPW時降低1.3%的效能)。中心圓的半徑為4個畫素時最好，但3或5畫素結果相似。將伸展因子從2增加到3效能不會變化。為細胞單元的投票加上高斯權重或逆高斯權重不會改變效能。形狀上下文方向(只含一個方向bin)需要更精細的空間子劃分才能表現良好。

       塊歸一化策略

       我們對上面介紹的每種幾何形狀的塊都測試了四種歸一化方法。

       假設v是未經歸一化的描述子向量。

       ‖v‖_k是v的k範數，k=1,2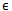，是一個很小的常數

       (L2 norm就是平方和開方，即歐氏距離；L1 norm就是絕對值相加，又稱曼哈頓距離)

       (a)L2-norm(L2範數)：

       (b)L2-Hys：先計算L2範數，然後進行限幅(限制v的最大值為0.2)和再歸一化，[12]中有描述。

       (c)L1-norm(L1範數)：

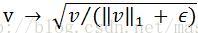
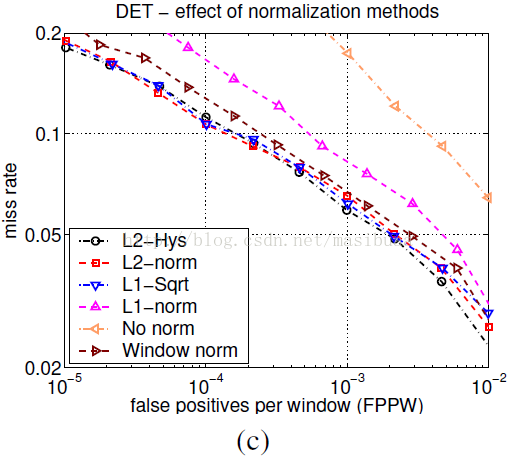
       (d)L1-sqrt：L1範數取平方根，即，實際上是將描述子向量看作是概率分佈，然後計算它們之間的Bhattacharya(巴氏)距離。

       如圖4(c)所示，L2-Hys、L2-norm、L1-sqrt的表現差不多一樣好，簡單的L1-norm會使效能下降5%，如果完全不進行歸一化會導致效能下降27%(都是指10^-4FPPW時)。我們還調整引數的值進行測試，但結果表明檢測器效能對於值的變化並不敏感。

圖4(c)

 

       中心環繞歸一化

       我們研究了中心環繞式的細胞單元歸一化方法，利用每個細胞單元和環繞其周圍的細胞單元(利用二維高斯權重進行加權)的能量對該細胞單元進行歸一化，然而結果如圖4(c)中的”Window norm”曲線所示，這種方法相比於基於塊的歸一化方法會使效能下降(在10^-4FPPW時降低2%)。其中一個原因是由於沒有重疊的塊，每個細胞單元僅在最終的描述子中被使用一次。改變高斯加權的引數也並不會引起結果的變化。

       為了闡明這點，考慮有重疊塊的R-HOG檢測器。訓練好的線性SVM分類器的引數會衡量每個塊中的每個細胞單元在最終的判定決策中起多少作用。圖6(b,f)表明最重要的細胞單元是包含主要的人體輪廓(特別是頭部、肩部和足部)的那些，用這些細胞單元相對於輪廓外的塊進行歸一化。也就是說，不管訓練圖片中的背景如何複雜，檢測器檢測的主要是人體輪廓相對於背景的差異，而不是內部的邊緣或輪廓相對於前景的差異。衣服上的圖案和身體姿勢的變化使得人體輪廓內部的區域不適合作為可靠的檢測特徵，而且前景到輪廓的過度可能由於平滑陰影而混淆。圖6(c,g)表明人體輪廓內部的梯度(尤其是垂直梯度)一般都是有害的特徵，可能是因為這些特徵會引起誤報，在這些誤報中長的垂直條紋會被當做頭部或腿。

圖6，HOG描述子最有用的資訊來自於人體輪廓周圍(尤其是頭部、肩部、足部)，最有效的塊是以人體輪廓外沿的背景為中心的那些塊。(a)訓練樣本的平均梯度圖，(b)每個畫素表示塊中以此畫素為中心的最大正SVM權重，(c)與(b)類似，負SVM權重，(d)一張測試圖，(e)計算得到的R-HOG描述子，(f)正SVM權重支援的R-HOG描述子，(g)負SVM權重支援的R-HOG描述子

 

6.5 檢測視窗和上下文

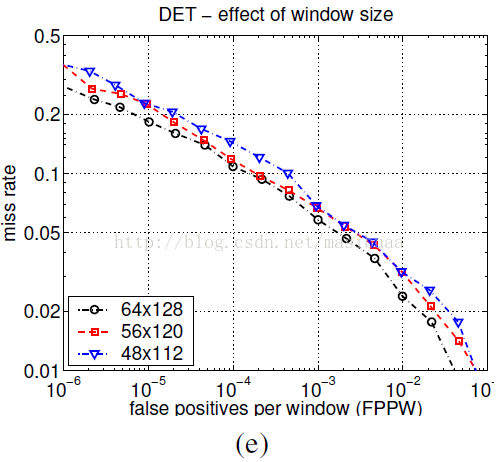
       我們用的64*128大小的檢測視窗在人體周圍會產生大約16個畫素的空白邊緣。圖4(e)表明此空白邊緣增加了有助於檢測的上下文資訊。將空白邊緣從16畫素減少到8畫素(48*112大小的檢測視窗)會在10^-4FPPW時導致6%的效能下降。保持視窗大小為64*128不變，增加人體的尺寸(同樣會使空白邊緣減少)，雖然使得人體的解析度變高，但也會導致效能下降。

圖4(e)

 

6.6 分類器

       我們預設使用帶有鬆弛變數(C=0.01)的線性SVM分類器SVMLight[10](在原版SVM上稍作改動使得處理大規模特徵向量時可減少記憶體佔用)。如果使用高斯核函式SVM可以在10^-4FPPW時提高大約3%的效能，但需要以更多的執行時間為代價。

 

6.7 討論

       總體來說，此篇論文中有幾個重要發現。HOG特徵表現遠好於小波，計算梯度前任何大尺度的平滑都會導致效能下降，大多數可用的影象資訊都來自精細尺度中的陡峭邊緣，為了減少對空間位置的敏感度而模糊陡峭邊緣的做法都是錯誤的。相反，梯度應該在最精細尺度的金字塔層中計算，然後進行校正或用於方向bin的投票，只有在投票時才需要進行模糊。據此，相對粗糙的空間取樣(8*8的細胞單元)也足夠用，但方向取樣需要相當精細，小波和形狀上下文正是輸在這點上。

       另外，較強的區域性對比度歸一化對於取得好的結果至關重要，傳統的中心環繞式歸一化方法並不太好。要想取得更好的結果，可在不同的區域性區域對每個元素(邊、細胞單元)歸一化多次。在我們的標準HOG檢測器中，每個細胞單元在不同的歸一化中出現4次，這種“冗餘”的方法可在10^-4FPPW時將效能由84%提高到89%。

 

7 總結和結論

       在稠密重疊網格中使用類似SIFT描述子[12]的區域性歸一化的梯度方向直方圖特徵對於行人檢測效果非常好，相比基於Haar小波特徵的最好的檢測器(來自[17])可以將誤報率降低一個多數量級。我們研究了各種描述子引數對結果的影響，得出結論：小尺度梯度(fine-scale gradients)，精細的方向取樣(fine orientation binning)，相對粗糙的空間取樣(relatively coarse spatialbinning)，和重疊描述子塊中高質量的區域性對比度歸一化(high-quality localcontrast normalization in overlapping descriptor blocks)都對好的檢測效果至關重要。我們還引入了一個新的更具挑戰性的行人檢測資料集，已公開下載。

       今後的工作

       雖然我們當前使用的線性SVM分類器已相當高效——處理一個320*240的尺度空間影象(4000個檢測視窗)的時間少於1秒鐘，但仍然有優化的空間。為了更深層次的加快檢測速度，需要一個由粗到細的或者拒絕鏈式的基於HOG的檢測器。我們也在研究基於HOG的，並同時包含基於塊匹配或光流的運動資訊的檢測器。最後，雖然當前的固定模版檢測器在全身可見的行人檢測方面有不可比擬的優勢，但由於人體是高度關節型的，所以我們相信具有更好的區域性空間不變性的基於身體部分的模型可以在更一般的場景中改善行人檢測效果。

       致謝

       此研究得到了歐洲聯合研究專案組ACEMEDIA和PASCAL的支援。感謝Cordelia Schmid的大量有用建議。SVM-Light[10]保證了大規模樣本訓練的可靠性。

論文下載地址：http://download.csdn.net/detail/masikkk/6492599