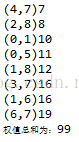Java 經典演算法分析總彙
前言
在計算機軟體專業中,演算法分析與設計是一門非常重要的課程,很多人為它如痴如醉。很多問題的解決,程式的編寫都要依賴它,在軟體還是程式導向的階段,就有‘程式=演算法+資料結構’這個公式。演算法的學習對於培養一個人的邏輯思維能力是有極大幫助的,它可以培養 我們養成思考分析問題,解決問題的能力。 如果一個演算法有缺陷,或不適合某個問題,執行這個演算法將不會解決這個問題。不同的演算法可能用不同的時間、空間或效率來完成同樣的任務。一個演算法的優劣可以用空間複雜性和時間複雜度來衡量。演算法可以使用自然語言、虛擬碼、流程圖等多種不同的方法來描述。計算機系統中的作業系統、語言編譯系統、資料庫管理系統以及各種各樣的計算機應用系統中的軟體,都必須使用具體的演算法來實現。演算法設計與分析是電腦科學與技術的一個核心問題。因此,學習演算法無疑會增強自己的競爭力,提高自己的修為,為自己增彩。
演算法概念:
演算法簡單來說就是指解題方案的準確而完整的描述,是一系列解決問題的清晰指令,也就是說演算法告訴計算機怎麼做,以此來解決問題。同一個問題存在多種演算法來解決它,但是這些演算法存在著優劣之分,好的演算法速度快,效率高,佔用空間小,差的演算法不僅複雜難懂,而且效率低,對機器要求還高,當然,有時候演算法之間存在一種互補關係,有些演算法效率高,節省時間,但浪費空間,另外一些演算法可能速度上慢些,但是空間比較節約,這時候 我們就應該根據實際要求,和具體情況來採取相應的演算法來解決問題。
一、約瑟夫演算法
約瑟夫環:已知n個人(以編號1,2,3...n分別表示)圍坐在一張圓桌周圍。從編號為k的人開始報數,數到m的那個人出列;他的下一個人又從1開始報數,數到m的那個人又出列;依此規律重複下去,直到圓桌周圍的人全部出列。
- public class YuesefuTest {
- public static void main(String[] args) {
- int totalNum = 10;
- int countNum = 3;
- yuesefuByMyself(totalNum, countNum);
- yuesefu(totalNum, countNum);
- }
- /**
- * 此方法 k 為 list 的下標
- * @param totalNum
- * @param countNum
- */
- public static void yuesefuByMyself( int totalNum,int countNum){
- // 初始化人數
- List<Integer> start = new ArrayList<Integer>();
- for(int i=1; i<=totalNum; i++){
- start.add(i);
- }
- // 此處的k為list的下標,開始報數人的下標,第一個人為0,第n個人為n-1
- int k = 0;
- while(start.size()>0){
- // 下一個出列人的下標,因為是從當前報數人開始數,所以減1為下一個出列人的下標
- k = k + countNum -1;
- // 當 下標+1 超過了 list 的size
- if(k + 1>start.size()){
- // 當size 為 10 ,下標要取 10 ,最大下標為9,應該取 list 的 第一個,即下標為0,
- // 同理,直接取餘即可為正確下標
- k = k % start.size();
- }
- System.out.print(start.get(k)+",");
- // 出列,下一個開始報數人的下標即為出列人的下標
- start.remove(k);
- }
- System.out.println();
- }
- public static void yuesefu(int totalNum,int countNum){
- // 初始化人數
- List<Integer> start = new ArrayList<Integer>();
- for(int i=1; i<=totalNum; i++){
- start.add(i);
- }
- // 從第K個開始計數
- int k = 0;
- while(start.size()>0){
- k = k + countNum;
- // 第m人的索引位置
- k = k % (start.size()) -1;
- // 判斷是否到隊尾
- if(k<0){
- System.out.print(start.get(start.size()-1)+",");
- start.remove(start.size()-1);
- k = 0;
- } else {
- System.out.print(start.get(k)+",");
- start.remove(k);
- }
- }
- System.out.println();
- }
- }

public class BinaryTree {
private static String [] array = {"A","B","D","H","","","I","","","E","","J","","",
"C","F","","K","","","G","",""};
private static int arrayIndex = 0;
// 建立一棵二叉樹,約定使用者遵照前序遍歷的方式輸入資料
// 不使用迭代是因為迭代必須要知道這棵樹有多深,
// 遞迴只需要輸入就可以自行決定深度
// type:結點型別 0 根節點 1左孩子 2右孩子
public static TreeNode createBinaryTree(int type,String parentData) {
switch (type) {
case 0:
System.out.print("根節點:");
break;
case 1:
System.out.print(parentData+"的左孩子:");
break;
case 2:
System.out.print(parentData+"的右孩子:");
break;
}
// 可以使用手動輸入也可以放到陣列裡
// Scanner sc = new Scanner(System.in);
// String data = sc.nextLine();
String data = "";
if(arrayIndex<array.length){
data = array[arrayIndex];
System.out.println(data);
arrayIndex++;
}else{
System.out.println();
}
TreeNode node = null;
// data為空表示沒有這個孩子
if(data==null||data.equals("")){
return node;
}else{
node = new TreeNode(data);
node.setLchild(createBinaryTree(1,node.getData()));
node.setRchild(createBinaryTree(2,node.getData()));
return node;
}
}
// 前序遍歷
public static void preOrderTraverse(TreeNode node){
if(node != null){
// 根,左,右
System.out.print(node.getData());
preOrderTraverse(node.getLchild());
preOrderTraverse(node.getRchild());
}
}
// 中序遍歷
public static void inOrderTraverse(TreeNode node){
if(node != null){
// 左,根,右
inOrderTraverse(node.getLchild());
System.out.print(node.getData());
inOrderTraverse(node.getRchild());
}
}
// 後序遍歷
public static void postOrderTraverse(TreeNode node){
if(node != null){
// 左,右,根
postOrderTraverse(node.getLchild());
postOrderTraverse(node.getRchild());
System.out.print(node.getData());
}
}
//
public static void main(String[] args) {
TreeNode rootNode = createBinaryTree(0,"");
System.out.println();
System.out.print("前序遍歷:");
preOrderTraverse(rootNode);
System.out.println();
System.out.print("中序遍歷:");
inOrderTraverse(rootNode);
System.out.println();
System.out.print("後序遍歷:");
postOrderTraverse(rootNode);
}
}
/**
* 二叉樹結點
* @author cmdsm
*
*/
class TreeNode{
private String data;
private TreeNode lchild;
private TreeNode rchild;
public TreeNode() {
super();
}
public TreeNode(String data) {
this.data = data;
}
public String getData() {
return data;
}
public void setData(String data) {
this.data = data;
}
public TreeNode getLchild() {
return lchild;
}
public void setLchild(TreeNode lchild) {
this.lchild = lchild;
}
public TreeNode getRchild() {
return rchild;
}
public void setRchild(TreeNode rchild) {
this.rchild = rchild;
}
@Override
public String toString() {
return "TreeNode [data=" + data + ", lchild=" + lchild + ", rchild=" + rchild + "]";
}
} 三、線索二叉樹(中序)
程式碼所示為下圖二叉樹
中序遍歷:CBDAEF
C,D,F有兩個空指標域,E有一個
步驟如下:
1.建立二叉樹
2.建立頭結點
3.中序遍歷線索化
4.中序遍歷此線索二叉樹(非遞迴方式)
public class ThreadedBinaryTree {
private static String [] array = {"A","B","C","","","D","","","E","","F","",""};
private static int arrayIndex = 0;
/**
* 全域性node,始終指向剛剛訪問過的結點
*/
private static ThreadedBinaryNode preNode;
/**
* 1.參考建立二叉樹,前序遍歷輸入
*/
public static ThreadedBinaryNode createThreadedBinaryTree(){
String data = "";
if(arrayIndex<array.length){
data = array[arrayIndex];
arrayIndex++;
}
ThreadedBinaryNode node = null;
// data為空表示沒有這個孩子
if(data==null||data.equals("")){
return node;
}else{
node = new ThreadedBinaryNode(data);
node.setLchild(createThreadedBinaryTree());
node.setRchild(createThreadedBinaryTree());
node.setLtag(PointerTag.LINK);
node.setRtag(PointerTag.LINK);
return node;
}
}
/**
* 2.建立頭結點,左孩子指向根節點
* @param rootNode
*/
public static ThreadedBinaryNode createHeadNode(ThreadedBinaryNode rootNode){
ThreadedBinaryNode headNode = new ThreadedBinaryNode();
headNode.setLtag(PointerTag.LINK);
headNode.setRtag(PointerTag.THREAD);
// 右孩子先指向自己,如果根節點不為null,指向中序遍歷的最後一個結點,為null不用變
headNode.setRchild(headNode);
if(rootNode != null){
// 根結點不為null,頭結點的左孩子指向根結點
headNode.setLchild(rootNode);
preNode = headNode;
// 開始中序遍歷根結點
inOrderTraverse(rootNode);
// 中序遍歷的最後一個結點的後繼指向頭結點
preNode.setRtag(PointerTag.THREAD);
preNode.setRchild(headNode);
// 頭結點的右孩子指向最後一個結點
headNode.setRchild(preNode);
}else{
// 根節點為null 左孩子指向自己
headNode.setLchild(headNode);
}
return headNode;
}
/**
* 3.中序遍歷線索化
*/
public static void inOrderTraverse(ThreadedBinaryNode node){
if(node != null){
// 遞迴左孩子線索化
inOrderTraverse(node.getLchild());
// 結點處理
if(null == node.getLchild()){
// 如果左孩子為空,設定tag為線索 THREAD,並把lchild指向剛剛訪問的結點
node.setLtag(PointerTag.THREAD);
node.setLchild(preNode);
}
if(null == preNode.getRchild()){
// 如果preNode的右孩子為空,設定tag為線索THREAD
preNode.setRtag(PointerTag.THREAD);
preNode.setRchild(node);
}
// 此處和前後兩個遞迴的順序不能改變,和結點處理同屬一個級別
preNode = node;
// System.out.print(node.getData());
// 遞迴右孩子線索化
inOrderTraverse(node.getRchild());
}
}
/**
* 4.中序遍歷 非遞迴方式
* @param headNode
*/
public static void inOrderTraverseNotRecursion(ThreadedBinaryNode headNode){
ThreadedBinaryNode node = headNode.getLchild();
while(headNode != node){
// 最左
while(node.getLtag() == PointerTag.LINK){
node = node.getLchild();
}
System.out.print(node.getData());
// 根
while(node.getRtag() == PointerTag.THREAD && node.getRchild() !=headNode){
node = node.getRchild();
System.out.print(node.getData());
}
// 右,不能列印是因為該子樹下可能還存在最左
node = node.getRchild();
}
}
public static void main(String[] args) {
// 建立二叉樹,約定前序輸入
ThreadedBinaryNode rootNode = createThreadedBinaryTree();
// 建立頭結點,並中序遍歷線索化
ThreadedBinaryNode headNode = createHeadNode(rootNode);
// 中序遍歷 非遞迴方式輸出
inOrderTraverseNotRecursion(headNode);
}
}
class ThreadedBinaryNode{
private String data;
private ThreadedBinaryNode lchild;
private ThreadedBinaryNode rchild;
private PointerTag ltag;
private PointerTag rtag;
public String getData() {
return data;
}
public void setData(String data) {
this.data = data;
}
public ThreadedBinaryNode getLchild() {
return lchild;
}
public void setLchild(ThreadedBinaryNode lchild) {
this.lchild = lchild;
}
public ThreadedBinaryNode getRchild() {
return rchild;
}
public void setRchild(ThreadedBinaryNode rchild) {
this.rchild = rchild;
}
public PointerTag getLtag() {
return ltag;
}
public void setLtag(PointerTag ltag) {
this.ltag = ltag;
}
public PointerTag getRtag() {
return rtag;
}
public void setRtag(PointerTag rtag) {
this.rtag = rtag;
}
public ThreadedBinaryNode(String data) {
super();
this.data = data;
}
public ThreadedBinaryNode() {
super();
}
@Override
public String toString() {
return "ThreadedBinaryNode [data=" + data + ", ltag=" + ltag
+ ", rtag=" + rtag + "]";
}
}
/**
* LINK :表示指向左右孩子的指標
* THREAD:表示指向前驅後繼的線索
* @author cmdsm
*
*/
enum PointerTag{
LINK , THREAD
}
四、普里姆(Prim)演算法
個人認為此演算法遍歷順序的決定條件:
1.確定第一個頂點
2.下一個頂點可到(小於正無窮)
3.取可到頂點中最小權值的一個
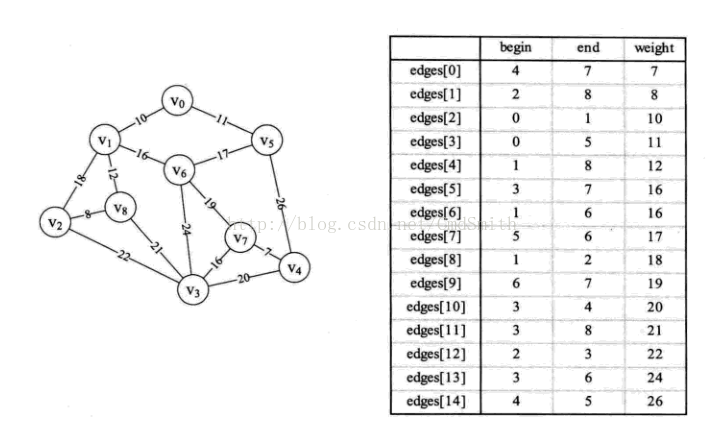
程式碼中的圖
最小生成樹:99
程式碼(參考其他文章):
public class MinSpanTree {
/** 鄰接矩陣*/
int[][] matrix;
/** 表示正無窮*/
int MAX_WEIGHT = Integer.MAX_VALUE;
/** 頂點個數*/
int size;
/**
* 普里姆演算法實現最小生成樹:先初始化拿到第一個頂點相關聯的權值元素放到陣列中-》找到其中權值最小的頂點下標-》再根據該下標,將該下標頂點相關聯的權值加入到陣列中-》迴圈遍歷處理
*/
public void prim() {
/**存放當前到全部頂點最小權值的陣列,如果已經遍歷過的頂點權值為0,無法到達的為正無窮*/
int[] tempWeight = new int[size];
/**當前到下一個最小權值頂點的最小權值*/
int minWeight;
/**當前到下一個最小權值的頂點*/
int minId;
/**權值總和*/
int sum = 0;
//第一個頂點時,到其他頂點的權值即為鄰接矩陣的第一行
for (int i = 0; i < size; i++) {
tempWeight[i] = matrix[0][i];
}
System.out.println("從頂點v0開始查詢");
for (int i = 1; i < size; i++) {
// 每次迴圈找出當前到下一個最小權值的頂點極其最小權值
minWeight = MAX_WEIGHT;
minId = 0;
for (int j = 1; j < size; j++) {
//權值為0的頂點已經遍歷過,不再計入
if (tempWeight[j] > 0 && tempWeight[j] < minWeight) {
minWeight = tempWeight[j];
minId = j;
}
}
// 找到目標頂點minId,他的權值為minweight。
System.out.println("找到頂點:v" + minId + " 權值為:" + minWeight);
sum += minWeight;
// 演算法核心所在:將目標頂點到各個頂點的權值與當前tempWeight陣列中的權值做比較,如果前者比後者到某個頂點的權值更小,將前者到這個頂點的權值更新入後者。
tempWeight[minId] = 0;
for (int j = 1; j < size; j++) {
if (tempWeight[j] != 0 && matrix[minId][j] < tempWeight[j]) {
tempWeight[j] = matrix[minId][j];
}
}
}
System.out.println("最小權值總和為:" + sum);
}
private void createGraph(int index) {
size = index;
matrix = new int[index][index];
int[] v0 = { 0, 10, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] v1 = { 10, 0, 18, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, MAX_WEIGHT, 12 };
int[] v2 = { MAX_WEIGHT, 18, 0, 22, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 8 };
int[] v3 = { MAX_WEIGHT, MAX_WEIGHT, 22, 0, 20, MAX_WEIGHT, MAX_WEIGHT, 16, 21 };
int[] v4 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 20, 0, 26, MAX_WEIGHT, 7, MAX_WEIGHT };
int[] v5 = { 11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 26, 0, 17, MAX_WEIGHT, MAX_WEIGHT };
int[] v6 = { MAX_WEIGHT, 16, MAX_WEIGHT, 24, MAX_WEIGHT, 17, 0, 19, MAX_WEIGHT };
int[] v7 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, 7, MAX_WEIGHT, 19, 0, MAX_WEIGHT };
int[] v8 = { MAX_WEIGHT, 12, 8, 21, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 0 };
matrix[0] = v0;
matrix[1] = v1;
matrix[2] = v2;
matrix[3] = v3;
matrix[4] = v4;
matrix[5] = v5;
matrix[6] = v6;
matrix[7] = v7;
matrix[8] = v8;
}
public static void main(String[] args) {
MinSpanTree graph = new MinSpanTree();
graph.createGraph(9);
graph.prim();
}
} 判斷是否為迴路的機制沒有理解
程式碼所示圖和邊集陣列
程式碼:
public class MiniSpanTreeKruskal {
/** 鄰接矩陣 */
private int[][] matrix;
/** 表示正無窮 */
private int MAX_WEIGHT = Integer.MAX_VALUE;
/**邊集陣列*/
private List<Edge> edgeList = new ArrayList<Edge>();
/**
* 建立圖
*/
private void createGraph(int index) {
matrix = new int[index][index];
int[] v0 = { 0, 10, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] v1 = { 10, 0, 18, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, MAX_WEIGHT, 12 };
int[] v2 = { MAX_WEIGHT, 18, 0, 22, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 8 };
int[] v3 = { MAX_WEIGHT, MAX_WEIGHT, 22, 0, 20, MAX_WEIGHT, MAX_WEIGHT, 16, 21 };
int[] v4 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 20, 0, 26, MAX_WEIGHT, 7, MAX_WEIGHT };
int[] v5 = { 11, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 26, 0, 17, MAX_WEIGHT, MAX_WEIGHT };
int[] v6 = { MAX_WEIGHT, 16, MAX_WEIGHT, 24, MAX_WEIGHT, 17, 0, 19, MAX_WEIGHT };
int[] v7 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 16, 7, MAX_WEIGHT, 19, 0, MAX_WEIGHT };
int[] v8 = { MAX_WEIGHT, 12, 8, 21, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 0 };
matrix[0] = v0;
matrix[1] = v1;
matrix[2] = v2;
matrix[3] = v3;
matrix[4] = v4;
matrix[5] = v5;
matrix[6] = v6;
matrix[7] = v7;
matrix[8] = v8;
}
/**
* 建立邊集陣列,並且對他們按權值從小到大排序(順序儲存結構也可以認為是陣列吧)
*/
public void createEdages() {
Edge v0 = new Edge(4, 7, 7);
Edge v1 = new Edge(2, 8, 8);
Edge v2 = new Edge(0, 1, 10);
Edge v3 = new Edge(0, 5, 11);
Edge v4 = new Edge(1, 8, 12);
Edge v5 = new Edge(3, 7, 16);
Edge v6 = new Edge(1, 6, 16);
Edge v7 = new Edge(5, 6, 17);
Edge v8 = new Edge(1, 2, 18);
Edge v9 = new Edge(6, 7, 19);
Edge v10 = new Edge(3, 4, 20);
Edge v11 = new Edge(3, 8, 21);
Edge v12 = new Edge(2, 3, 22);
Edge v13 = new Edge(3, 6, 24);
Edge v14 = new Edge(4, 5, 26);
edgeList.add(v0);
edgeList.add(v1);
edgeList.add(v2);
edgeList.add(v3);
edgeList.add(v4);
edgeList.add(v5);
edgeList.add(v6);
edgeList.add(v7);
edgeList.add(v8);
edgeList.add(v9);
edgeList.add(v10);
edgeList.add(v11);
edgeList.add(v12);
edgeList.add(v13);
edgeList.add(v14);
}
// 克魯斯卡爾演算法
public void kruskal() {
//建立圖和邊集陣列
createGraph(9);
//可以由圖轉出邊集陣列並按權從小到大排序,這裡為了方便觀察直接寫出來了
createEdages();
//定義一個陣列用來判斷邊與邊是否形成環路
int[] parent = new int[9];
/**權值總和*/
int sum = 0;
int n, m;
//遍歷邊
for (int i = 0; i < edgeList.size(); i++) {
Edge edge= edgeList.get(i);
n = find(parent, edge.getBegin());
m = find(parent, edge.getEnd());
//說明形成了環路或者兩個結點都在一棵樹上
//注:書上沒有講解為什麼這種機制可以保證形成環路,思考了半天,百度了也沒有什麼好的答案,研究的時間不多,就暫時就放一放吧
if (n != m) {
parent[n] = m;
System.out.println("(" + edge.getBegin() + "," + edge.getEnd() + ")" +edge.getWeight());
sum += edge.getWeight();
}
}
System.out.println("權值總和為:" + sum);
}
public int find(int[] parent, int index) {
while (parent[index] > 0) {
index = parent[index];
}
return index;
}
public static void main(String[] args) {
MiniSpanTreeKruskal graph = new MiniSpanTreeKruskal();
graph.kruskal();
}
}
class Edge {
private int begin;
private int end;
private int weight;
public Edge(int begin, int end, int weight) {
super();
this.begin = begin;
this.end = end;
this.weight = weight;
}
public int getBegin() {
return begin;
}
public void setBegin(int begin) {
this.begin = begin;
}
public int getEnd() {
return end;
}
public void setEnd(int end) {
this.end = end;
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
@Override
public String toString() {
return "Edge [begin=" + begin + ", end=" + end + ", weight=" + weight + "]";
}
} 結果:
六、迪傑斯特拉(Dijkstra)演算法
基本思想
通過Dijkstra計算圖G中的最短路徑時,需要指定起點vs(即從頂點vs開始計算)。
此外,引進兩個集合S和U。S的作用是記錄已求出最短路徑的頂點,而U則是記錄還未求出最短路徑的頂點(以及該頂點到起點vs的距離)。
初始時,S中只有起點vs;U中是除vs之外的頂點,並且U中頂點的路徑是"起點vs到該頂點的路徑"。然後,從U中找出路徑最短的頂點,並將其加入到S中;接著,更新U中的頂點和頂點對應的路徑。 然後,再從U中找出路徑最短的頂點,並將其加入到S中;接著,更新U中的頂點和頂點對應的路徑。 ... 重複該操作,直到遍歷完所有頂點。
操作步驟
(1) 初始時,S只包含起點vs;U包含除vs外的其他頂點,且U中頂點的距離為"起點vs到該頂點的距離"[例如,U中頂點v的距離為(vs,v)的長度,然後vs和v不相鄰,則v的距離為∞]。
(2) 從U中選出"距離最短的頂點k",並將頂點k加入到S中;同時,從U中移除頂點k。
(3) 更新U中各個頂點到起點vs的距離。之所以更新U中頂點的距離,是由於上一步中確定了k是求出最短路徑的頂點,從而可以利用k來更新其它頂點的距離;例如,(vs,v)的距離可能大於(vs,k)+(k,v)的距離。
(4) 重複步驟(2)和(3),直到遍歷完所有頂點。
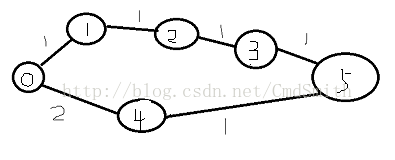
程式碼示例圖:
圖一:
圖二:
程式碼:
public class ShortestPathDijkstra {
/** 鄰接矩陣 */
private int[][] matrix;
/** 表示正無窮 */
private int MAX_WEIGHT = Integer.MAX_VALUE;
/** 頂點集合 */
private String[] vertexes;
/**
* 建立圖2
*/
private void createGraph2(int index) {
matrix = new int[index][index];
vertexes = new String[index];
int[] v0 = { 0, 1, 5, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] v1 = { 1, 0, 3, 7, 5, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] v2 = { 5, 3, 0, MAX_WEIGHT, 1, 7, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] v3 = { MAX_WEIGHT, 7, MAX_WEIGHT, 0, 2, MAX_WEIGHT, 3, MAX_WEIGHT, MAX_WEIGHT };
int[] v4 = { MAX_WEIGHT, 5, 1, 2, 0, 3, 6, 9, MAX_WEIGHT };
int[] v5 = { MAX_WEIGHT, MAX_WEIGHT, 7, MAX_WEIGHT, 3, 0, MAX_WEIGHT, 5, MAX_WEIGHT };
int[] v6 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 3, 6, MAX_WEIGHT, 0, 2, 7 };
int[] v7 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 9, 5, 2, 0, 4 };
int[] v8 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 7, 4, 0 };
matrix[0] = v0;
matrix[1] = v1;
matrix[2] = v2;
matrix[3] = v3;
matrix[4] = v4;
matrix[5] = v5;
matrix[6] = v6;
matrix[7] = v7;
matrix[8] = v8;
vertexes[0] = "v0";
vertexes[1] = "v1";
vertexes[2] = "v2";
vertexes[3] = "v3";
vertexes[4] = "v4";
vertexes[5] = "v5";
vertexes[6] = "v6";
vertexes[7] = "v7";
vertexes[8] = "v8";
}
/**
* 建立圖1
*/
private void createGraph1(int index) {
matrix = new int[index][index];
vertexes = new String[index];
int[] v0 = { 0, 1, MAX_WEIGHT, MAX_WEIGHT, 2, MAX_WEIGHT };
int[] v1 = { 1, 0, 1, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] v2 = { MAX_WEIGHT, 1, 0, 1, MAX_WEIGHT, MAX_WEIGHT };
int[] v3 = { MAX_WEIGHT, MAX_WEIGHT, 1, 0, 1, MAX_WEIGHT };
int[] v4 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 1, 0, 1 };
int[] v5 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 1, 1, 0 };
matrix[0] = v0;
matrix[1] = v1;
matrix[2] = v2;
matrix[3] = v3;
matrix[4] = v4;
matrix[5] = v5;
vertexes[0] = "A";
vertexes[1] = "B";
vertexes[2] = "C";
vertexes[3] = "D";
vertexes[4] = "E";
vertexes[5] = "F";
}
/**
* Dijkstra最短路徑。
*
* vs -- 起始頂點(start vertex) 即,統計圖中"頂點vs"到其它各個頂點的最短路徑。
*/
public void dijkstra(int vs) {
// flag[i]=true表示"頂點vs"到"頂點i"的最短路徑已成功獲取
boolean[] flag = new boolean[vertexes.length];
// U則是記錄還未求出最短路徑的頂點(以及該頂點到起點s的距離),與 flag配合使用,flag[i] == true 表示U中i頂點已被移除
int[] U = new int[vertexes.length];
// 前驅頂點陣列,即,prev[i]的值是"頂點vs"到"頂點i"的最短路徑所經歷的全部頂點中,位於"頂點i"之前的那個頂點。
int[] prev = new int[vertexes.length];
// S的作用是記錄已求出最短路徑的頂點
String[] S = new String[vertexes.length];
// 步驟一:初始時,S中只有起點vs;U中是除vs之外的頂點,並且U中頂點的路徑是"起點vs到該頂點的路徑"。
for (int i = 0; i < vertexes.length; i++) {
flag[i] = false; // 頂點i的最短路徑還沒獲取到。
U[i] = matrix[vs][i]; // 頂點i與頂點vs的初始距離為"頂點vs"到"頂點i"的權。也就是鄰接矩陣vs行的資料。
prev[i] = 0; //頂點i的前驅頂點為0
}
// 將vs從U中“移除”(U與flag配合使用)
flag[vs] = true;
U[vs] = 0;
// 將vs頂點加入S
S[0] = vertexes[vs];
// 步驟一結束
//步驟四:重複步驟二三,直到遍歷完所有頂點。
// 遍歷vertexes.length-1次;每次找出一個頂點的最短路徑。
int k = 0;
for (int i = 1; i < vertexes.length; i++) {
// 步驟二:從U中找出路徑最短的頂點,並將其加入到S中(如果vs頂點到x頂點還有更短的路徑的話,那麼
// 必然會有一個y頂點到vs頂點的路徑比前者更短且沒有加入S中
// 所以,U中路徑最短頂點的路徑就是該頂點的最短路徑)
// 即,在未獲取最短路徑的頂點中,找到離vs最近的頂點(k)。
int min = MAX_WEIGHT;
for (int j = 0; j < vertexes.length; j++) {
if (flag[j] == false && U[j] < min) {
min = U[j];
k = j;
}
}
//將k放入S中
S[i] = vertexes[k];
//步驟二結束
//步驟三:更新U中的頂點和頂點對應的路徑
//標記"頂點k"為已經獲取到最短路徑(更新U中的頂點,即將k頂點對應的flag標記為true)
flag[k] = true;
//修正當前最短路徑和前驅頂點(更新U中剩餘頂點對應的路徑)
//即,當已經"頂點k的最短路徑"之後,更新"未獲取最短路徑的頂點的最短路徑和前驅頂點"。
for (int j = 0; j < vertexes.length; j++) {
//以k頂點所在位置連線其他頂點,判斷其他頂點經過最短路徑頂點k到達vs頂點是否小於目前的最短路徑,是,更新入U,不是,不做處理
int tmp = (matrix[k][j] == MAX_WEIGHT ? MAX_WEIGHT : (min + matrix[k][j]));
if (flag[j] == false && (tmp < U[j])) {
U[j] = tmp;
//更新 j頂點的最短路徑前驅頂點為k
prev[j] = k;
}
}
//步驟三結束
}
//步驟四結束
// 列印dijkstra最短路徑的結果
System.out.println("起始頂點:" + vertexes[vs]);
for (int i = 0; i < vertexes.length; i++) {
System.out.print("最短路徑(" + vertexes[vs] + "," + vertexes[i] + "):" + U[i] + " ");
List<String> path = new ArrayList<>();
int j = i;
while (true) {
path.add(vertexes[j]);
if (j == 0)
break;
j = prev[j];
}
for (int x = path.size()-1; x >= 0; x--) {
if (x == 0) {
System.out.println(path.get(x));
} else {
System.out.print(path.get(x) + "->");
}
}
}
System.out.println("頂點放入S中的順序:");
for (int i = 0; i< vertexes.length; i++) {
System.out.print(S[i]);
if (i != vertexes.length-1)
System.out.print("-->");
}
}
public static void main(String[] args) {
ShortestPathDijkstra dij = new ShortestPathDijkstra();
dij.createGraph1(6);
// dij.createGraph2(9);
dij.dijkstra(0);
}
} 執行結果:
圖一
圖二
七、弗洛伊德(Floyd)演算法
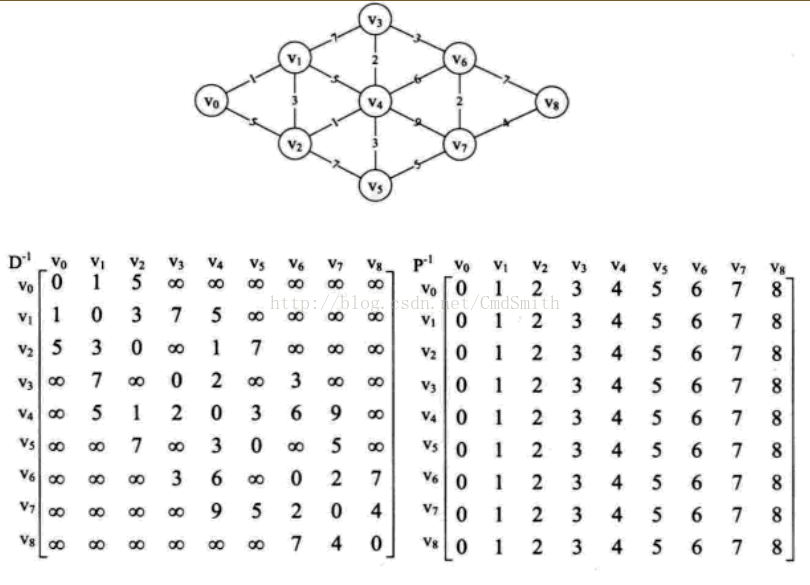
程式碼所示圖:
圖1:
圖2:
程式碼:
public class ShortestPathFloyd {
/** 鄰接矩陣 */
private int[][] matrix;
/** 表示正無窮 */
private int MAX_WEIGHT = Integer.MAX_VALUE;
/**路徑矩陣*/
private int[][] pathMatirx;
/**前驅表*/
private int[][] preTable;
/**
* 建立圖2
*/
private void createGraph2(int index) {
matrix = new int[index][index];
int[] v0 = { 0, 1, 5, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] v1 = { 1, 0, 3, 7, 5, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] v2 = { 5, 3, 0, MAX_WEIGHT, 1, 7, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] v3 = { MAX_WEIGHT, 7, MAX_WEIGHT, 0, 2, MAX_WEIGHT, 3, MAX_WEIGHT, MAX_WEIGHT };
int[] v4 = { MAX_WEIGHT, 5, 1, 2, 0, 3, 6, 9, MAX_WEIGHT };
int[] v5 = { MAX_WEIGHT, MAX_WEIGHT, 7, MAX_WEIGHT, 3, 0, MAX_WEIGHT, 5, MAX_WEIGHT };
int[] v6 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 3, 6, MAX_WEIGHT, 0, 2, 7 };
int[] v7 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 9, 5, 2, 0, 4 };
int[] v8 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 7, 4, 0 };
matrix[0] = v0;
matrix[1] = v1;
matrix[2] = v2;
matrix[3] = v3;
matrix[4] = v4;
matrix[5] = v5;
matrix[6] = v6;
matrix[7] = v7;
matrix[8] = v8;
}
/**
* 建立圖1
*/
private void createGraph1(int index) {
matrix = new int[index][index];
int[] v0 = { 0, 1, MAX_WEIGHT, MAX_WEIGHT, 2, MAX_WEIGHT };
int[] v1 = { 1, 0, 1, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT };
int[] v2 = { MAX_WEIGHT, 1, 0, 1, MAX_WEIGHT, MAX_WEIGHT };
int[] v3 = { MAX_WEIGHT, MAX_WEIGHT, 1, 0, 1, MAX_WEIGHT };
int[] v4 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 1, 0, 1 };
int[] v5 = { MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 1, 1, 0 };
matrix[0] = v0;
matrix[1] = v1;
matrix[2] = v2;
matrix[3] = v3;
matrix[4] = v4;
matrix[5] = v5;
}
public void floyd(){
//路徑矩陣(D),表示頂點到頂點的最短路徑權值之和的矩陣,初始時,就是圖的鄰接矩陣。
pathMatirx = new int[matrix.length][matrix.length];
//前驅表(P),P[m][n] 的值為 m到n的最短路徑的前驅頂點,如果是直連,值為n。也就是初始值
preTable = new int[matrix.length][matrix.length];
//初始化D,P
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix.length; j++) {
pathMatirx[i][j] = matrix[i][j];
preTable[i][j] = j;
}
}
//迴圈 中間經過頂點
for (int k = 0; k < matrix.length; k++) {
//迴圈所有路徑
for (int m = 0; m < matrix.length; m++) {
for (int n = 0; n < matrix.length; n++) {
int mn = pathMatirx[m][n];
int mk = pathMatirx[m][k];
int kn = pathMatirx[k][n];
int addedPath = (mk == MAX_WEIGHT || kn == MAX_WEIGHT)? MAX_WEIGHT : mk + kn;
if (mn > addedPath) {
//如果經過k頂點路徑比原兩點路徑更短,將兩點間權值設為更小的一個
pathMatirx[m][n] = addedPath;
//前驅設定為經過下標為k的頂點
preTable[m][n] = preTable[m][k];
}
}
}
}
}
/**
* 列印 所有最短路徑
*/
public void print() {
for (int m = 0; m < matrix.length; m++) {
for (int n = m + 1; n < matrix.length; n++) {
int k = preTable[m][n];
System.out.print("(" + m + "," + n + ")" + pathMatirx[m][n] + ": ");
System.out.print(m);
while (k != n) {
System.out.print("->" + k);
k = preTable[k][n];
}
System.out.println("->" + n);
}
System.out.println();
}
}
public static void main(String[] args) {
ShortestPathFloyd floyd = new ShortestPathFloyd();
floyd.createGraph2(9);
// floyd.createGraph1(6);
floyd.floyd();
floyd.print();
} 結果:
圖1:
圖2:
(0,1)1: 0->1
(0,2)4: 0->1->2
(0,3)7: 0->1->2->4->3
(0,4)5: 0->1->2->4
(0,5)8: 0->1->2->4->5
(0,6)10: 0->1->2->4->3->6
(0,7)12: 0->1->2->4->3->6->7
(0,8)16: 0->1->2->4->3->6->7->8
(1,2)3: 1->2
(1,3)6: 1->2->4->3
(1,4)4: 1->2->4
(1,5)7: 1->2->4->5
(1,6)9: 1->2->4->3->6
(1,7)11: 1->2->4->3->6->7
(1,8)15: 1->2->4->3->6->7->8
(2,3)3: 2->4->3
(2,4)1: 2->4
(2,5)4: 2->4->5
(2,6)6: 2->4->3->6
(2,7)8: 2->4->3->6->7
(2,8)12: 2->4->3->6->7->8
(3,4)2: 3->4
(3,5)5: 3->4->5
(3,6)3: 3->6
(3,7)5: 3->6->7
(3,8)9: 3->6->7->8
(4,5)3: 4->5
(4,6)5: 4->3->6
(4,7)7: 4->3->6->7
(4,8)11: 4->3->6->7->8
(5,6)7: 5->7->6
(5,7)5: 5->7
(5,8)9: 5->7->8
(6,7)2: 6->7
(6,8)6: 6->7->8
(7,8)4: 7->8 相關文章
- 經典Java面試題彙總及答案解析Java面試題
- 阿里歷年經典Java面試題彙總阿里Java面試題
- Spark 經典面試題彙總《一》Spark面試題
- Vue經典開源專案彙總Vue
- 經典:程式設計面試的 10 大演算法概念彙總程式設計面試演算法
- Java十大經典排序演算法最強總結Java排序演算法
- Vue.js經典開源專案彙總Vue.js
- 高薪運維經典企業版面試題彙總高薪運維面試題
- 前端面試經典題目彙總(持續更新中)前端面試
- 阿里歷年經典Java面試題彙總,想進BAT你還不快收藏!阿里Java面試題BAT
- 經典機器學習演算法總結機器學習演算法
- 《暗黑2》經典數值公式分析總結公式
- Java經典常用類總結(必須掌握!)Java
- 電子技術經典資料彙總:PCB設計篇
- 大彙總 | 一文學會八篇經典CNN論文CNN
- 經典 backbone 總結
- 文章經典總結
- 25道經典Java演算法題(含程式碼)Java演算法
- AQS:JAVA經典之鎖實現演算法(一)AQSJava演算法
- 十大經典排序演算法最強總結(含JAVA程式碼實現)排序演算法Java
- 【演算法與資料結構】經典排序演算法總結演算法資料結構排序
- Lisp經典演算法Lisp演算法
- MySQL經典案例分析MySql
- 電子技術經典資料彙總:模電篇800M
- 電子技術經典資料彙總:手機/移動裝置
- 最經典四級英語詞彙
- Java類集框架詳細彙總-底層分析Java框架
- AQS:JAVA經典之鎖實現演算法(二)-ConditionAQSJava演算法
- 經典排序演算法的 C語言 | Java 實現排序演算法C語言Java
- 演算法型別大總結(並附經典題型)演算法型別
- Python經典演算法片段Python演算法
- 122個經典SOTA模型、447個演算法實現資源,我們幫你一文彙總了模型演算法
- 面經and重點彙總
- Java基礎經典案例Java
- java經典面試題Java面試題
- 電子技術經典資料彙總:嵌入式開發12.9G
- 經典排序演算法回顧:排序演算法
- Linux 效能分析工具彙總Linux
- Java 實現彙總排序Java排序