ACM UVa演算法題209 Triangular Vertices的解法

ATField發表於2007-05-03
ACM演算法Angular

有一段時間沒有做ACM演算法題目了，今天正好有空便隨便挑了209題來做做：ACM UVa演算法題#209題

這道題有幾個要點：

1.   給定座標系

座標系很容易定，我採用的是第一個點為(0, 0)點，X方向差別為2個單位，Y方向差別為1個單位，點之間的距離，也就是LEN為1個單位，這樣便於計算。注意我用的不是實際長度，而是抽象的單位，這個單位在不同方向上面意義不一樣，否則很容易通過三角形相關公理推出這樣的三角形不存在，我們關心的只是這樣的一個對應關係。這裡的人為設定確實有些Confusing，我之前也是按照一般的三角形的長度，如3，4，5來定義，但是後來發現這樣做做的乘除法太多，過於浪費CPU Cycle，如果按照我這樣的設定，大部分情況只用到加減法，另外一種情況只需用到移位操作即可。

參看下圖：

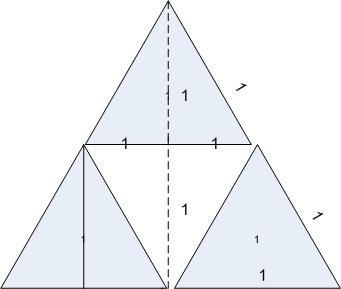
2.   判斷是否兩點連線是一條邊(Coincide)

這裡可以分兩種情況：

a.   Y1 = y2, 必然是Coincide

b.   否則，X_Delta = abs(x1 – x2), Y_Delta = abs(y1 – y2)， 由於之前我們人為設定X方向差別為2個單位，Y方向差別為1一個單位，因此只要X_Delta = Y_Delta即可

 

3.   計算距離

假定是Coincide的情況，否則直接返回出錯，因為在非Coincide的情況無需計算距離。此外，由於這裡已經知道是Coincide，並且我們並沒有統一單位，所以這裡不能也不應該用勾股定理來計算長度，而是採用比例的方法，同樣分兩種情況，參考上圖：

a.   Y1 = y2, 那麼因為X方向上兩個單位對應一個長度Unit，所以長度=abs(x1 – x2) >> 1;

b.   否則，長度Unit的個數和X/Y方向（任意）的差別相等，也就是長度=abs(x1 – x2)

 

4.   判斷是否是目標圖形，並且每條邊相等

對於三角形，很簡單，直接對3條邊判斷即可，沒有什麼變數。對於四邊形和六邊形就不同了，需要用到遍歷來確定一個從某點開始（我們可以固定為第一個點）遍歷所有點最後回到該點的環，並且每條邊長度均相等，注意這裡由於題目的特殊性，不用判斷平行等條件。可以用一個鄰接矩陣來代表對應的邊的長度，這個應該一次性計算出來，如果非Coincide則設定為某個特殊值，比如0

剛開始提交的時候，Rank是45，之後我又做了下面的優化：

1.   當遍歷嘗試完畢從最初點出發的某條邊的時候，說明這一邊不可能成為環，將其置為0表示不可通，並且遍歷從最初點出發的其他同樣長度的邊，置為0，減少遍歷次數

2.   在初始化計算所有點的座標的時候改變了一點點演算法，用加減法代替乘法

3.   最初座標採用的是實際的長度，而不是像上面那樣用不同的抽象單位算出，修改之後減少了大量乘除法計算

4.   調整遍歷演算法，由於從初始點出發之後，後3個點必然不能是初始點，因此做了一點修改對這個情況作了優化

5.   修改對鄰接矩陣的演算法，由於adj[i][j] = adj[j][i]，所以只需計算矩陣的一半即可

修改之後再提交Rank變成了33，似乎是目前個人的最好紀錄 J

32

0.170

792

 LittleJohn Yo

C

2002-02-04 07:02:47

732386

33

0.172

1160

 Yi Zhang

C++

2007-05-02 16:05:54

5551868

34

0.174

404

 Rodrigo Malta Schmidt

C

2001-08-30 08:46:54

539862
 
程式碼如下：
// 
// ACM UVa Problem #209
// http://acm.uva.es/p/v2/209.html
//
// Author:  ATField
// Email:   atfield_zhang@hotmail.com
//

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAX    65535

struct point
{
public :
    bool is_coincide(const point &pt) const
    {
        // not allow testing points with same coordinates
        if( _x == pt._x && _y == pt._y )
            return false;

        if( _y == pt._y )
            return true;
        else
        {
            int k1 = abs( _x - pt._x );
            int k2 = abs( _y - pt._y );

            if( k1 == k2 )
                return true;
        }

        return false;
    }

    int get_dist(const point &pt) const
    {
        // not allow testing points with same coordinates
        if( _x == pt._x && _y == pt._y )
            return 0;

        if( _y == pt._y )
            return abs(_x - pt._x) >> 1;        // need to divide by 2
        else
        {
            int k1 = abs( _x - pt._x );
            int k2 = abs( _y - pt._y );

            if( k1 == k2 )
                return k1;
        }

        return 0;
    }

public :
    static const int X_DELTA = 2;
    static const int Y_DELTA = 3;
    static const int LEN = 4;

public :
    int        _x;
    int        _y;
    int     _valid;

private :
    static point s_all_points[MAX];

public :
    static void prepare()
    {
        int level = 0;
        int before_next_level = 1;
        int next_x = 0;
        int next_y = 0;

        for( int i = 1; i < MAX ; ++i )
        {
            s_all_points[i]._x = next_x;
            s_all_points[i]._y = next_y;
            before_next_level--;

            if( before_next_level == 0 )
            {
                level++;
                before_next_level = level + 1;
                next_x = -level;
                next_y++;
            }
            else
                next_x += 2;

        }


    }

    static point *all_points()
    {
        return s_all_points;
    }
};

point point::s_all_points[MAX];

bool check_triangle(int *n)
{
    // 1. Duplicates
    // No need to check duplicate because the following checks will do

    // 2. Coincide
    // Check every edge
    point *points = point::all_points();
    if( points[n[0]].is_coincide(points[n[1]]) &&
        points[n[0]].is_coincide(points[n[2]]) &&
        points[n[1]].is_coincide(points[n[2]]) )
    {
        // 3. Same length
        // Check every edge
        int len = points[n[0]].get_dist(points[n[1]]);
        if( len == points[n[0]].get_dist(points[n[2]]) &&
            len == points[n[1]].get_dist(points[n[2]]) )
            return true;
    }

    return false;
}


bool init_adj(int *n, int num, int adj[6][6])
{
    point *points = point::all_points();

    for( int i = 0; i < num; ++i )
    {
        for( int j = i; j < num; ++j )
        {
            if( i == j )
            {
                adj[i][j] = 0;
                adj[j][i] = 0;
            }
            else
            {
                // 1. Duplicates
                // Return false when found duplicate
                if( n[i] == n[j] )
                    return false;

                // 2. Coincide & Len (When not coincide, len = 0)
                adj[i][j] = points[n[i]].get_dist(points[n[j]]);
                adj[j][i] = adj[i][j];
            }
        }
    }
        

    return true;
}

int find_same_len_loop(int adj[6][6], int num)
{
    int stack[6];
    int used[6];
    int next[6];

    for( int i = 1; i < num; ++i )
    {         
        int len = adj[0][i];

        // skip non-connected dots
        if( len == 0 ) continue;

        // initialize "used" array & "next" array
        for( int j = 0; j < num; ++j )
        {
            used[j] = 0;
        }        
        
        int top = 0;
        stack[0] = i;
        used[i] = 1;
        next[0] = -1;

        top++;

        while( top > 0 )
        {
            next[top-1]++;

            // checked all the connected points?
            if( next[top-1] >= num )
            {
                // yes, then pop the stack
                top--;
                used[stack[top]] = 0;
            }
            else
            {
                int next_point = next[top-1];

                // follow non-used, same-length edge
                if( used[next_point] == 0 && len == adj[stack[top-1]][next_point] )
                {
                    stack[top] = next_point;
                    used[next_point] = 1;

                    // don't allow pushing 0 into stack before the last point
                    if( top < num - 1 ) 
                        next[top] = 0;
                    else
                        next[top] = -1;

                    top++;

                    // stack is full? found a loop
                    if( top == num )
                        return len;
                }
            }
        }

        // if this doesn't work, delete all edges starting from id 0 of this len
        for( int j = i; j < num; ++j )
            if( adj[0][j] == len )
                adj[0][j] = 0;
    }

    return 0;
}

bool check_parallelogram(int *n)
{
    int adj[6][6];
    if(!init_adj(n, 4, adj))
        return false;           // found duplicate

    if(find_same_len_loop(adj, 4))
        return true;

    return false;
}

bool check_hexagon(int *n)
{
    int adj[6][6];
    if(!init_adj(n, 6, adj))
        return false;           // found duplicate

    if(find_same_len_loop(adj, 6))
        return true;

    return false;
}

int main(int argc, char *argv[])
{
    point::prepare();
    
    while(1)
    {
        char input[255];
        if( gets(input) == NULL )
            break;
        else if( strlen(input) == 0 )
            break;
        
        int n[6];
        int fields = sscanf( input, "%d %d %d %d %d %d", &n[0], &n[1], &n[2], &n[3], &n[4], &n[5] );

        printf("%s ", input);                    

        switch(fields)
        {
            case 3:
                {
                    bool is_triangle = check_triangle(n);

                    if( is_triangle )
                    {
                        puts("are the vertices of a triangle");
                        continue;
                    }

                    break;
                }

            case 4:
                {
                    bool is_parallelogram = check_parallelogram(n);

                    if( is_parallelogram )
                    {
                        puts("are the vertices of a parallelogram");
                        continue;
                    }

                    break;
                }

            case 6:
                {
                    bool is_hexagon = check_hexagon(n);

                    if( is_hexagon )
                    {
                        puts("are the vertices of a hexagon");
                        continue;
                    }

                    break;
                }
        }

        puts("are not the vertices of an acceptable figure");

    }

    return 0;
}

相關文章