【Stanford CNN課程筆記】4. 反向傳播演算法

本課程筆記是基於今年史丹佛大學Feifei Li, Andrej Karpathy & Justin Johnson聯合開設的Convolutional Neural Networks for Visual Recognition課程的學習筆記。目前課程還在更新中，此學習筆記也會盡量根據課程的進度來更新。

---

1. 引子

在這一章中，我們將介紹backpropagation,也就是反向傳播演算法，理解這一過程對於學習神經網路很重要。
之前的章節中我們定義了一個loss function，它是輸入資料x和網路引數W的函式，我們希望通過調節W使得網路的loss最小——這在Optimazation那一節中講過，通過梯度下降法來更新W。但是神經網路是一個多層的結構，直接用輸出對輸入求導計算非常複雜，因此我們會用到反向傳播演算法來進行逐層的梯度傳播與更新。

---

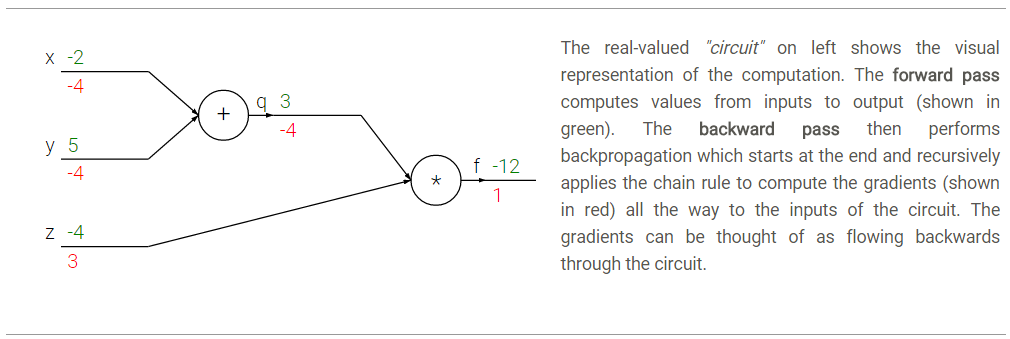
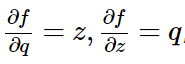
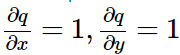
我們先來簡單地回顧一下偏導數的計算和鏈式法則。比如函式f(x,y,z)=(x+y)*z, 為了求得f對三個輸入x,y,z的偏導（即梯度），我們可以首先把它看成一個兩層的組合函式，分解成q=x+y,f=q*z。這樣逐層地計算偏導數就簡單了：；其中q又是x和y的函式，對x,y的偏導數又可以寫成。
那麼根據鏈式法則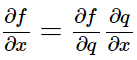，，也就是說輸出對輸入的偏導可以通過兩層網路組合得到。如下圖，假設我們代入x=-2,y=5,z=-4,計算上述函式f的值和導數分別如圖中綠色數字和紅色數字所示。我們可以發現計算值的過程是從輸入向輸出逐層計算，我們稱為前向傳播；而計算導數的過程則是從輸出向輸入逐層計算得，稱為反向傳播。

注意每一層的閘電路都能夠獨立地根據區域性的輸入計算當前閘電路的輸出以及區域性的梯度，而不需要去考慮其他層的操作。

• 比如以“+”門為例，輸入為x=-2,y=5,計算得輸出為3（前向傳播），又由於進行的是加法運算，因此，對於兩個輸入的區域性梯度均為+1（反向傳播）。
• 接著進行“∗
  *
  ”門的運算，此時輸入為上一層的輸出q=3，及z=-4，相乘得到最終輸出為-12，又由於進行的是乘法運算，，對於兩個輸入的區域性梯度分別為z和q，即-4和3。
• 那麼在反向傳播過程中，區域性梯度會通過鏈式法得到最終梯度，即，因此最終f對x的偏導就是兩個閘電路的區域性梯度相乘，也就是1*-4=-4。梯度為負表示的意思是如果x,y減小，則+門的輸出會減小，而最終*門的輸出會增大。

說了這麼多，主要想表達的意思就是 通過鏈式法則進行逐層的梯度反向傳播，你get到了嗎？

2. Sigmoid function

任何可微函式都可以看成門運算，並且我們還可以把多個門組合成一個，讓我們來看一個常用的函式，叫做sigmoid啟用函式：

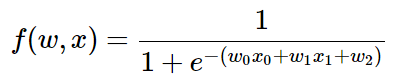
這個表示式包含w和x 2個輸入，我們可以把這個複雜的表示式拆分成多層的閘電路的組合：

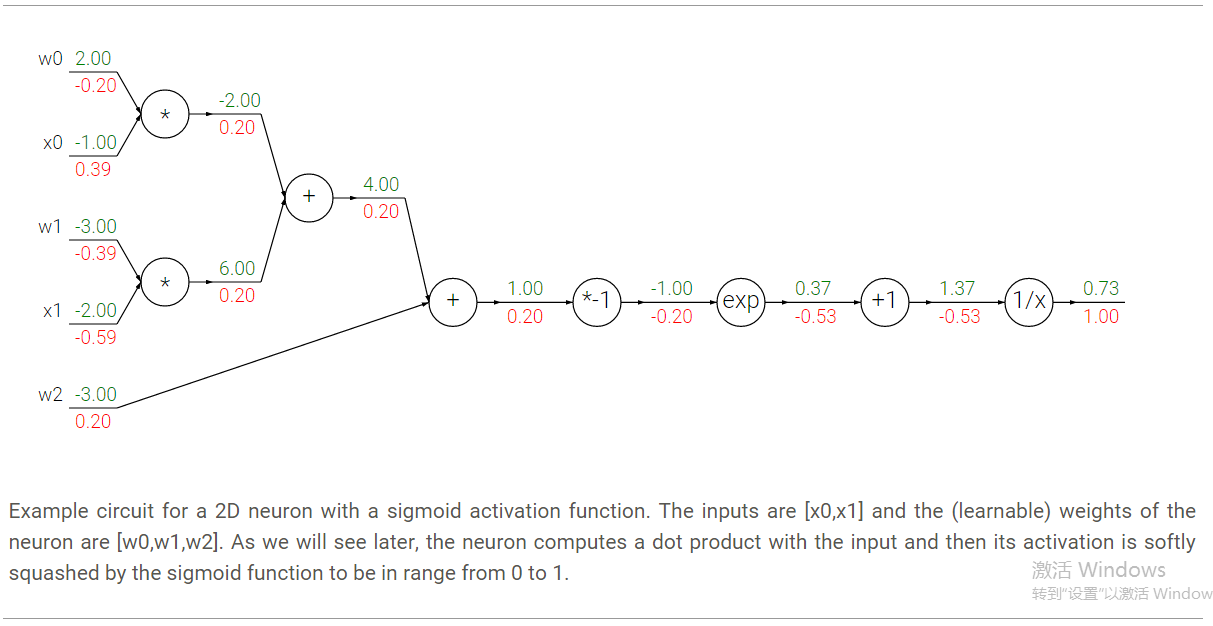
其中不同門的偏導數如下，

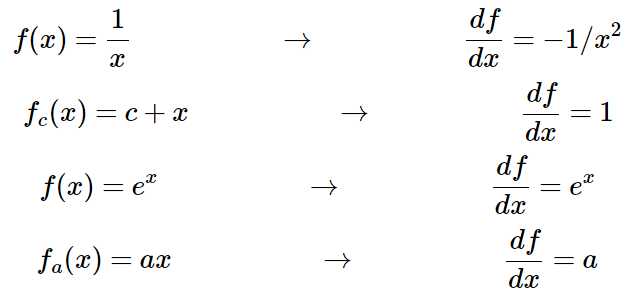
在這個例子中我們看到7層的一個網路，但其實我們可以把其中的部分看成一個整體：

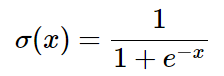
這整個表示式叫做sigmoid function，對它求偏導很簡單：

因此我們會把一連串的運算組合成一個sigmoid門，那麼反向傳播演算法是這樣的：

w = [2,-3,-3] # assume some random weights and data
x = [-1, -2]

# forward pass
dot = w[0]*x[0] + w[1]*x[1] + w[2]
f = 1.0 / (1 + math.exp(-dot)) # sigmoid function

# backward pass through the neuron (backpropagation)
ddot = (1 - f) * f # gradient on dot variable, using the sigmoid gradient derivation
dx = [w[0] * ddot, w[1] * ddot] # backprop into x
dw = [x[0] * ddot, x[1] * ddot, 1.0 * ddot] # backprop into w
# we're done! we have the gradients on the inputs to the circuit

3. 反向傳播程式碼實現

現在我們來舉一個例子具體得說明如何進行反向傳播的運算。f(x,y)如下式，注意我們並不需要顯式地去計算∂f/∂x

或∂f/∂y,我們只需要知道如何對這個函式進行拆分，然後分層計算區域性梯度再利用鏈式法則進行整合即可。

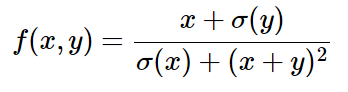
在前向傳播中，我們將整個等式進行如下拆分：

x = 3 # example values
y = -4

# forward pass
sigy = 1.0 / (1 + math.exp(-y)) # sigmoid in numerator   #(1)
num = x + sigy # numerator                               #(2)
sigx = 1.0 / (1 + math.exp(-x)) # sigmoid in denominator #(3)
xpy = x + y                                              #(4)
xpysqr = xpy**2                                          #(5)
den = sigx + xpysqr # denominator                        #(6)
invden = 1.0 / den                                       #(7)
f = num * invden # done!                                 #(8)

那麼通過上述程式碼，我們其實是把整個函式拆分成了多個簡單的表示式，每個表示式相當於之前所說的一個門，這些簡單的表示式使得我們可以很方便地計算區域性梯度。這樣在進行反向傳播時只需將區域性梯度相乘，在下面的程式碼中每個區域性梯度用d…表示：

# backprop f = num * invden
dnum = invden # gradient on numerator                             #(8)
dinvden = num                                                     #(8)
# backprop invden = 1.0 / den 
dden = (-1.0 / (den**2)) * dinvden                                #(7)
# backprop den = sigx + xpysqr
dsigx = (1) * dden                                                #(6)
dxpysqr = (1) * dden                                              #(6)
# backprop xpysqr = xpy**2
dxpy = (2 * xpy) * dxpysqr                                        #(5)
# backprop xpy = x + y
dx = (1) * dxpy                                                   #(4)
dy = (1) * dxpy                                                   #(4)
# backprop sigx = 1.0 / (1 + math.exp(-x))
dx += ((1 - sigx) * sigx) * dsigx # Notice += !! See notes below  #(3)
# backprop num = x + sigy
dx += (1) * dnum                                                  #(2)
dsigy = (1) * dnum                                                #(2)
# backprop sigy = 1.0 / (1 + math.exp(-y))
dy += ((1 - sigy) * sigy) * dsigy                                 #(1)
# done! phew

這樣在最後我們就實現了梯度的反向傳播。這裡需要注意兩點：
1.在進行前向傳播的過程中儲存好拆分變數是有必要的，這能夠幫助我們快速地在反向傳播過程中計算梯度。
2.前向傳播的過程中涉及多次x,y的使用，因此我們在反向傳播計算梯度時特別注意f對x,y的梯度是一個累加的過程（也就是說我們用的是+=，而不是=），這遵循了微分學中多變數的鏈式法則。

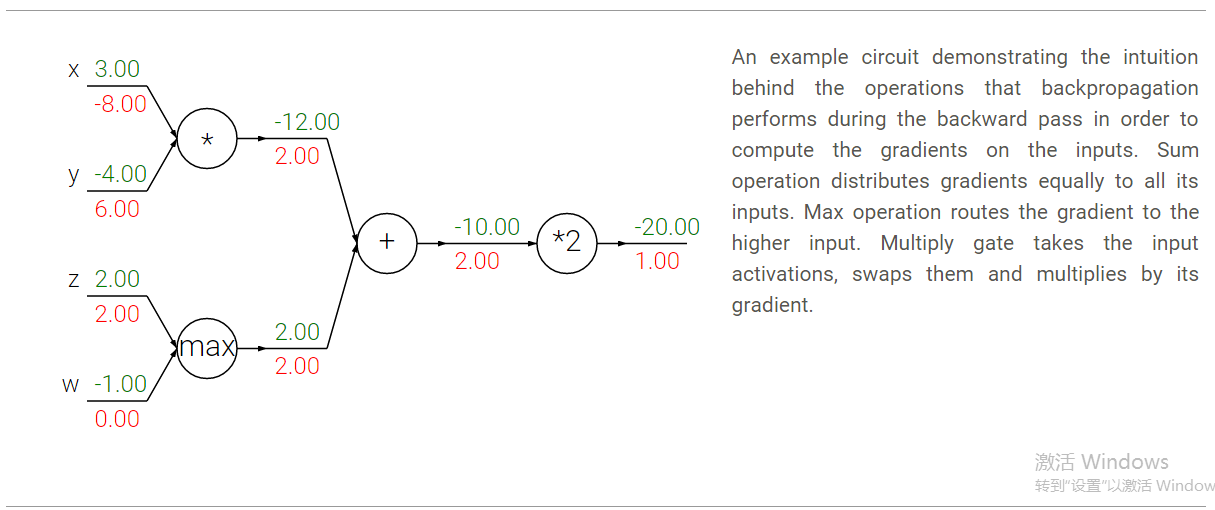
4. 反向傳播常用門的直觀理解

在反向傳播中幾個常用的閘電路，如+，*，max()，其實包含了一些實際的意義。比如以下圖的電路為例：

• +門的作用是將其輸出處接收到的梯度按原樣傳遞給其所有的輸入。這是因為加法的區域性梯度是1，所以輸入處的梯度=輸出的梯度*1，保持不變。在本例中，+門將2這個梯度反向傳播給了他的兩個輸入，使得這兩個輸入的梯度也同樣為2.
• max門的含義是梯度的選擇性。和+門的“平等對待”不同，max門選擇前向傳播過程中值最大的那個輸入來傳遞梯度，其他輸入梯度為0。在本例中，max門將2的梯度傳遞給了z和w中值更大的z，也就是z處的梯度為2，而w處的梯度為0.
• ∗
  *
  門則是將輸出的梯度乘以輸入的值得到輸入的梯度（不過乘的是除自己以外其他輸入的值）。比如上圖中x處的梯度-8，是由輸出梯度2，乘以另一個輸入值y（-4）得到的。另外對於∗
  *
  門還需要注意的一點是，如果這個門的一個輸入非常小，另一個輸入非常大，那麼∗
  *
  門就會給小的輸入一個較大的梯度，而給大的輸入一個很小的梯度。線上性分類器中常用的乘門是用於計算點乘wTxi
  w^Tx_i
  的，上述情況說明輸入x的數值範圍其實對於w的梯度的量級是有影響的。比如在預處理過程中給所有的訓練資料xi
  x_i
  都乘以1000，那麼w的梯度就會變成現有的1000倍，你就必須減小學習率來抵消這個因素。這就是為什麼預處理過程如歸一化等非常重要的原因，他會在很細微的地方影響我們的結果。

總結

我們對梯度的反向傳播進行了直觀的理解，它們是如何經過分層的計算最終得到輸出對輸入的梯度。這裡的重點就是在正向傳播的過程中對整個函式進行分層次的拆分，然後在反向傳播過程中計算每個閘電路的區域性梯度。在下一章中，我們將開始介紹神經網路。

參考

Automatic differentiation in machine learning: a survey