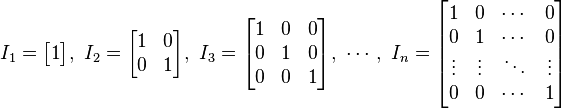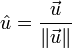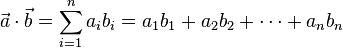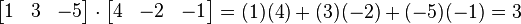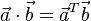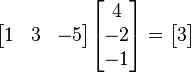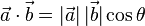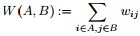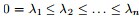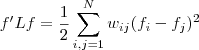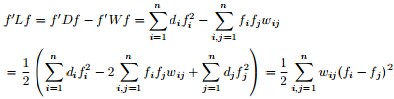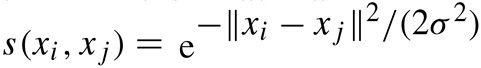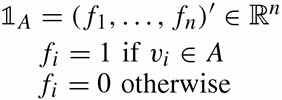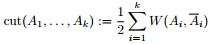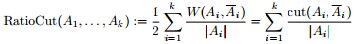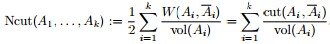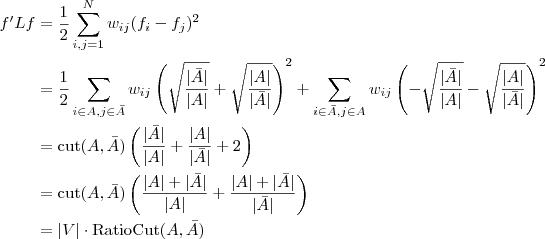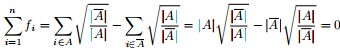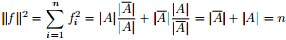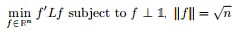從拉普拉斯矩陣說到譜聚類
從拉普拉斯矩陣說到譜聚類
0 引言
11月1日上午,機器學習班 第7次課,鄒講聚類(PPT),其中的譜聚類引起了自己的興趣,鄒從最基本的概念:單位向量、兩個向量的正交、方陣的特徵值和特徵向量,講到相似度圖、拉普拉斯矩陣,最後講譜聚類的目標函式和其演算法流程。
課後自己又琢磨了番譜聚類跟拉普拉斯矩陣,打算寫篇部落格記錄學習心得, 若有不足或建議,歡迎隨時不吝指出,thanks。
1 矩陣基礎
在講譜聚類之前,有必要了解一些矩陣方面的基礎知識。
1.0 理解矩陣的12點數學筆記
如果對矩陣的概念已經模糊,推薦國內一人寫的《理解矩陣by孟巖》系列,其中,丟擲了很多有趣的觀點,我之前在閱讀的過程中做了些筆記,如下:
“1、簡而言之:矩陣是線性空間裡的變換的描述,相似矩陣則是對同一個線性變換的不同描述。那,何謂空間?本質而言,“空間是容納運動的一個物件集合,而變換則規定了對應空間的運動”by孟巖。線上性空間選定基後,向量刻畫物件的運動,運動則通過矩陣與向量相乘來施加。然,到底什麼是基?座標系也。
3、前面說了基,座標系也,形象表述則為角度,看一個問題的角度不同,描述問題得到的結論也不同,但結論不代表問題本身,同理,對於一個線性變換,可以選定一組基,得到一個矩陣描述它,換一組基,得到不同矩陣描述它,矩陣只是描述線性變換非線性變換本身,類比給一個人選取不同角度拍照。
4、前面都是說矩陣描述線性變換,然,矩陣不僅可以用來描述線性變換,更可以用來描述基(座標系/角度),前者好理解,無非是通過變換的矩陣把線性空間中的一個點給變換到另一個點上去,但你說矩陣用來描述基(把一個座標系變換到另一個座標系),這可又是何意呢?實際上,變換點與變換座標系,異曲同工!
(@坎兒井圍脖:矩陣還可以用來描述微分和積分變換。關鍵看基代表什麼,用座標基就是座標變換。如果基是小波基或傅立葉基,就可以用來描述小波變換或傅立葉變換)
5、矩陣是線性運動(變換)的描述,矩陣與向量相乘則是實施運動(變換)的過程,同一個變換在不同的座標系下表現為不同的矩陣,但本質/徵值相同,運動是相對的,物件的變換等價於座標系的變換,如點(1,1)變到(2,3),一者可以讓座標點移動,二者可以讓X軸單位度量長度變成原來1/2,讓Y軸單位度量長度變成原來1/3,前後兩者都可以達到目的。
6、Ma=b,座標點移動則是向量a經過矩陣M所描述的變換,變成了向量b;變座標系則是有一個向量,它在座標系M的度量下結果為a,在座標系I(I為單位矩陣,主對角為1,其它為0)的度量下結果為b,本質上點運動與變換座標系兩者等價。為何?如(5)所述,同一個變換,不同座標系下表現不同矩陣,但本質相同。
7、Ib,I在(6)中說為單位座標系,其實就是我們常說的直角座標系,如Ma=Ib,在M座標系裡是向量a,在I座標系裡是向量b,本質上就是同一個向量,故此謂矩陣乘法計算無異於身份識別。且慢,什麼是向量?放在座標系中度量,後把度量的結果(向量在各個座標軸上投影值)按順序排列在一起,即成向量。
8、b在I座標系中則是Ib,a在M座標系中則是Ma,故而矩陣乘法MxN,不過是N在M座標系中度量得到MN,而M本身在I座標系中度量出。故Ma=Ib,M座標系中的a轉過來在I座標系中一量,卻成了b。如向量(x,y)在單位長度均為1的直角座標系中一量,是(1,1),而在X軸單位長度為2.Y軸單位長度為3一量則是(2,3)。
9、何謂逆矩陣? Ma=Ib,之前已明瞭座標點變換a-〉b等價於座標系變換M-〉I,但具體M如何變為I呢,答曰讓M乘以M的逆矩陣。以座標系
1.1 一堆基礎概念
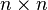 的方形矩陣,其主對角線元素為1,其餘元素為0。單位矩陣以
的方形矩陣,其主對角線元素為1,其餘元素為0。單位矩陣以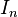 表示;如果階數可忽略,或可由前後文確定的話,也可簡記為
表示;如果階數可忽略,或可由前後文確定的話,也可簡記為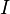 (或者E)。 如下圖所示,便是一些單位矩陣:
(或者E)。 如下圖所示,便是一些單位矩陣: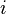 列即為單位向量
列即為單位向量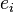 。單位向量同時也是單位矩陣的特徵向量,特徵值皆為1,因此這是唯一的特徵值,且具有重數n。由此可見,單位矩陣的行列式為1,且跡數為n。
。單位向量同時也是單位矩陣的特徵向量,特徵值皆為1,因此這是唯一的特徵值,且具有重數n。由此可見,單位矩陣的行列式為1,且跡數為n。 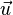 的正規化向量(即單位向量)
的正規化向量(即單位向量)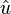 就是平行於
就是平行於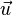 的單位向量,記作:
的單位向量,記作:這裡
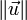 是
是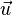 的範數(長度)。
的範數(長度)。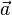 = [a1, a2,…, an]和
= [a1, a2,…, an]和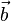 = [b1, b2,…, bn]的點積定義為:
= [b1, b2,…, bn]的點積定義為: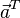 指示矩陣的轉置。使用上面的例子,將一個1×3矩陣(就是行向量)乘以一個3×1向量得到結果(通過矩陣乘法的優勢得到1×1矩陣也就是標量):
指示矩陣的轉置。使用上面的例子,將一個1×3矩陣(就是行向量)乘以一個3×1向量得到結果(通過矩陣乘法的優勢得到1×1矩陣也就是標量):除了上面的代數定義外,點積還有另外一種定義:幾何定義。在歐幾里得空間中,點積可以直觀地定義為:
這裡|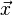
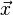
正交是垂直這一直觀概念的推廣,若內積空間中兩向量的內積(即點積)為0,則稱它們是正交的,相當於這兩向量垂直,換言之,如果能夠定義向量間的夾角,則正交可以直觀的理解為垂直。而正交矩陣(orthogonal matrix)是一個元素為實數,而且行與列皆為正交的單位向量的方塊矩陣(方塊矩陣,或簡稱方陣,是行數及列數皆相同的矩陣。)
 和非零向量
和非零向量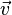 滿足
滿足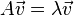 ,則
,則 為
為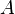 的一個特徵向量,
的一個特徵向量,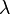 是其對應的特徵值。 換句話說,在
是其對應的特徵值。 換句話說,在 這個方向上,
這個方向上,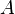 做的事情無非是把
做的事情無非是把 沿其
沿其 的方向拉長/縮短了一點(而不是毫無規律的多維變換),
的方向拉長/縮短了一點(而不是毫無規律的多維變換), 則是表示沿著這個方向上拉伸了多少的比例。 簡言之,
則是表示沿著這個方向上拉伸了多少的比例。 簡言之,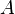 對
對 做了手腳,使得向量
做了手腳,使得向量 變長或變短了,但
變長或變短了,但 本身的方向不變。
本身的方向不變。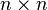 的對角線元素之和,也是其
的對角線元素之和,也是其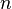 個特徵值之和。
個特徵值之和。 2 拉普拉斯矩陣
2.1 Laplacian matrix的定義
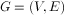 ,其拉普拉斯矩陣被定義為:
,其拉普拉斯矩陣被定義為: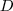 為圖的度矩陣,
為圖的度矩陣,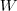 為圖的鄰接矩陣。
為圖的鄰接矩陣。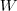 :
: 把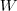
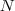

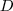
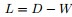 ,可得拉普拉斯矩陣
,可得拉普拉斯矩陣 為:
為:2.2 拉普拉斯矩陣的性質
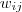 定義為節點
定義為節點 到節點
到節點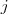 的權值,如果兩個節點不是相連的,權值為零。
的權值,如果兩個節點不是相連的,權值為零。②與某結點鄰接的所有邊的權值和定義為該頂點的度d,多個d 形成一個度矩陣
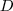 (對角陣)
(對角陣) 具有如下性質:
具有如下性質:是對稱半正定矩陣;
,即
的最小特徵值是0,相應的特徵向量是
。證明:
*
= (
-
) *
= 0 = 0 *
。(此外,別忘了,之前特徵值和特徵向量的定義:若數字
和非零向量
滿足
,則
為
的一個特徵向量,
是其對應的特徵值)。
有n個非負實特徵值
- 且對於任何一個屬於實向量
,有以下式子成立
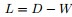 ,
,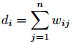 ,
,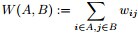 。
。3 譜聚類
- cut/Ratio Cut
- Normalized Cut
- 不基於圖,而是轉換成SVD能解的問題
3.1 相關定義
- 無向圖
,頂點集V表示各個樣本,帶權的邊表示各個樣本之間的相似度
- 與某結點鄰接的所有邊的權值和定義為該頂點的度d,多個d 形成一個度矩陣
(對角陣)
- 鄰接矩陣
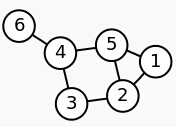
,A子圖與B子圖之間所有邊的權值之和定義如下:
其中,定義為節點
到節點
的權值,如果兩個節點不是相連的,權值為零。
- 相似度矩陣的定義。相似度矩陣由權值矩陣得到,實踐中一般用高斯核函式(也稱徑向基函式核)計算相似度,距離越大,代表其相似度越小。
- 子圖A的指示向量如下:
3.2 目標函式
 為圖的幾個子集(它們沒有交集) ,為了讓分割的Cut 值最小,譜聚類便是要最小化下述目標函式:
為圖的幾個子集(它們沒有交集) ,為了讓分割的Cut 值最小,譜聚類便是要最小化下述目標函式: 其中k表示分成k個組,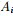
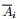
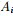
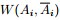
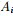
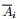
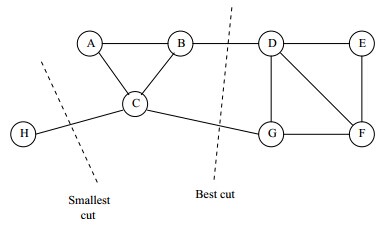
為了讓被切斷邊的權值之和最小,便是要讓上述目標函式最小化。但很多時候,最小化cut 通常會導致不好的分割。以分成2類為例,這個式子通常會將圖分成了一個點和其餘的n-1個點。如下圖所示,很明顯,最小化的smallest cut不是最好的cut,反而把{A、B、C、H}分為一邊,{D、E、F、G}分為一邊很可能就是最好的cut:
為了讓每個類都有合理的大小,目標函式儘量讓A1,A2...Ak 足夠大。改進後的目標函式為:
其中|A|表示A組中包含的頂點數目。
或:
其中,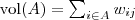
3.3 最小化RatioCut 與最小化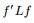 等價
等價
下面,我們們來重點研究下RatioCut 函式。
目標函式:
定義向量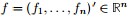
根據之前得到的拉普拉斯矩陣矩陣的性質,已知
現在把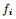
是的,我們竟然從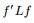
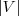
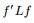
同時,因單位向量
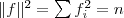
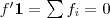
最終我們新的目標函式可以由之前的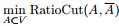
其中,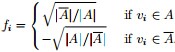
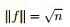
繼續推導前,再次提醒特徵向量和特徵值的定義:
- 若數字
和非零向量
滿足
,則
為
的一個特徵向量,
是其對應的特徵值。
假定
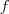

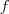

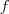

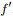
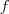
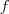
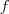

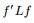



但到了這關鍵的最後一步,我們們卻遇到了一個比較棘手的問題,即由之前得到的拉普拉斯矩陣的性質“


因此,怎麼辦呢?根據論文“A Tutorial on Spectral Clustering”中所說的Rayleigh-Ritz 理論,我們可以取第2小的特徵值,以及對應的特徵向量
 裡的元素是連續的任意實數,所以可以根據
裡的元素是連續的任意實數,所以可以根據 是大於0,還是小於0對應到離散情況下的
是大於0,還是小於0對應到離散情況下的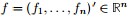 ,決定
,決定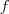 是取
是取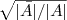 ,還是取
,還是取 。而如果能求取
。而如果能求取 的前K個特徵向量,進行K-means聚類,得到K個簇,便從二聚類擴充套件到了K 聚類的問題。
的前K個特徵向量,進行K-means聚類,得到K個簇,便從二聚類擴充套件到了K 聚類的問題。 就這樣,因為離散求解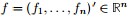
3.4 譜聚類演算法過程
綜上可得譜聚類的演算法過程如下:
- 根據資料構造一個Graph,Graph的每一個節點對應一個資料點,將各個點連線起來(隨後將那些已經被連線起來但並不怎麼相似的點,通過cut/RatioCut/NCut 的方式剪開),並且邊的權重用於表示資料之間的相似度。把這個Graph用鄰接矩陣的形式表示出來,記為
。
- 把
的每一列元素加起來得到
個數,把它們放在對角線上(其他地方都是零),組成一個
的對角矩陣,記為度矩陣
,並把
-
的結果記為拉普拉斯矩陣
。
- 求出
的前
個特徵值(前
個指按照特徵值的大小從小到大排序得到)
,以及對應的特徵向量
。
- 把這
個特徵(列)向量排列在一起組成一個
的矩陣,將其中每一行看作
維空間中的一個向量,並使用 K-means 演算法進行聚類。聚類的結果中每一行所屬的類別就是原來 Graph 中的節點亦即最初的
個資料點分別所屬的類別。
或許你已經看出來,譜聚類的基本思想便是利用樣本資料之間的相似矩陣(拉普拉斯矩陣)進行特徵分解( 通過Laplacian Eigenmap 的降維方式降維),然後將得到的特徵向量進行 K-means聚類。
此外,譜聚類和傳統的聚類方法(例如 K-means)相比,譜聚類只需要資料之間的相似度矩陣就可以了,而不必像K-means那樣要求資料必須是 N 維歐氏空間中的向量。
4 參考文獻與推薦閱讀
- 孟巖之理解矩陣系列:http://blog.csdn.net/myan/article/details/1865397;
- 理解矩陣的12點數學筆記:http://www.51weixue.com/thread-476-1-1.html;
- 一堆wikipedia,比如特徵向量:https://zh.wikipedia.org/wiki/%E7%89%B9%E5%BE%81%E5%90%91%E9%87%8F;
- wikipedia上關於拉普拉斯矩陣的介紹:http://en.wikipedia.org/wiki/Laplacian_matrix;
- 鄒博之聚類PPT:http://pan.baidu.com/s/1i3gOYJr;
- 關於譜聚類的一篇非常不錯的英文文獻,“A Tutorial on Spectral Clustering”:http://engr.case.edu/ray_soumya/mlrg/Luxburg07_tutorial_spectral_clustering.pdf;
- 知乎上關於矩陣和特徵值的兩個討論:http://www.zhihu.com/question/21082351,http://www.zhihu.com/question/21874816;
- 譜聚類:http://www.cnblogs.com/fengyan/archive/2012/06/21/2553999.html;
- 譜聚類演算法:http://www.cnblogs.com/sparkwen/p/3155850.html;
- 漫談 Clustering 系列:http://blog.pluskid.org/?page_id=78;
- 《Mining of Massive Datasets》第10章:http://infolab.stanford.edu/~ullman/mmds/book.pdf;
- Tydsh: Spectral Clustering:①http://blog.sina.com.cn/s/blog_53a8a4710100g2rt.html,②http://blog.sina.com.cn/s/blog_53a8a4710100g2rv.html,③http://blog.sina.com.cn/s/blog_53a8a4710100g2ry.html,④http://blog.sina.com.cn/s/blog_53a8a4710100g2rz.html;
- H. Zha, C. Ding, M. Gu, X. He, and H.D. Simon. Spectral relaxation for K-means clustering. Advances in Neural Information Processing Systems 14 (NIPS 2001). pp. 1057-1064, Vancouver, Canada. Dec. 2001;
- 機器學習中譜聚類方法的研究:http://lamda.nju.edu.cn/conf/MLA07/files/YuJ.pdf;
- 譜聚類的演算法實現:http://liuzhiqiangruc.iteye.com/blog/2117144。
相關文章
- 【機器學習】--譜聚類從初始到應用機器學習聚類
- 譜聚類原理總結聚類
- 從斐波那契到矩陣快速冪矩陣
- 【機器學習】---密度聚類從初識到應用機器學習聚類
- 譜聚類的python實現聚類Python
- 【機器學習】--層次聚類從初識到應用機器學習聚類
- 譜聚類(spectral clustering)原理總結聚類
- 用scikit-learn學習譜聚類聚類
- 從JavaScript中的類陣列物件說起JavaScript陣列物件
- 14聚類演算法-程式碼案例六-譜聚類(SC)演算法案例聚類演算法
- 矩陣類 poj3420矩陣
- 轉錄組上游-windows使用kallisto-從cleandata到表達矩陣Windows矩陣
- 生成螺旋矩陣(方陣、矩陣)矩陣
- 鄰接矩陣、度矩陣矩陣
- 巨大的矩陣(矩陣加速)矩陣
- (原創)一般矩陣 Matrix類矩陣
- 奇異矩陣,非奇異矩陣,偽逆矩陣矩陣
- [關係圖譜] 二.Gephi匯入共線矩陣構建作者關係圖譜矩陣
- 「管理數學基礎」1.7 矩陣理論:方陣特徵值估計、圓盤定理、譜與譜半徑矩陣特徵
- 用三列二維陣列表示的稀疏矩陣類陣列矩陣
- [NOIP 2024 模擬2]矩陣學說矩陣
- 圖˙譜˙馬爾可夫過程˙聚類結構----by林達華馬爾可夫聚類
- 矩陣矩陣
- 資料結構:陣列,稀疏矩陣,矩陣的壓縮。應用:矩陣的轉置,矩陣相乘資料結構陣列矩陣
- [關係圖譜] 一.Gephi通過共現矩陣構建知網作者關係圖譜矩陣
- 3D圖形:矩陣的行列式,矩陣的逆、正交矩陣、齊次矩陣3D矩陣
- 世界空間到觀察空間的矩陣矩陣
- 矩陣中最大的二維矩陣矩陣
- 求任意矩陣的伴隨矩陣矩陣
- python矩陣下標從幾開始?Python矩陣
- 《前端圖形學從入門到放棄》002 教練我想學矩陣前端矩陣
- 機器學習中的矩陣向量求導(五) 矩陣對矩陣的求導機器學習矩陣求導
- 矩陣和陣列矩陣陣列
- Flutter 45: 圖解矩陣變換 Transform 類 (二)Flutter圖解矩陣ORM
- 理解矩陣矩陣
- 矩陣相乘矩陣
- 矩陣分解矩陣
- 稀疏矩陣矩陣