20160128.CCPP體系詳解(0007天)

以下內容有所摘取,進行了某些整理和補充
論浮點數的儲存原理:float浮點數與double浮點數的二進位制儲存原理–>階碼
浮點數轉二進位制
1.整數int型別和浮點數float型別都是佔用4個位元組,在計算機中有32位來進行表示,那為什麼什麼float的範圍大於int？
答:因為兩者的儲存原理一樣,雖然該同樣是採用二進位制的方式進行儲存,但是整數型別(int)採用的是補碼方式進行儲存,但是浮點型別(float)採用的是階碼方式儲存.由於階碼內部的儲存原理和指數相關,所以採用同樣大小的二進位制碼可以表示更大範圍的浮點資料.
2.浮點數(float型別)的精度為6~7位,只有這個範圍內的浮點數才是精確的,只要過了這個位數的浮點數都存在可能精確和可能不精確的情況,比如1.66*10^10(指數形式的浮點數)轉化成為整數形式,所得到的結果並不是預期的結果16600000000,反而,描述實數的階碼(指數越大的等同原理)越大,誤差越大.
3.浮點數型別(float)和浮點數型別(double)在計算機當中的儲存方式都遵從IEEE的規範,而且兩種浮點型別在IEEE當中又有子規範型別,float遵從的是R32.24規範,double遵從的是R64.53規範
4.無論浮點型別是單精度(float)還是雙精度(double)在計算機當中的二進位制碼錶示都分為三個部分:
(1).符號位(Sign):0代表正數,1代表負數
無論是float還是double,符號位都只佔用一個二進位制位
(2).階碼位(Exponent):用於儲存科學計演算法中的指數資料,並且採用了移位儲存原理.
float的階碼位佔用8個二進位制位,double的階碼位佔用11個二進位制位
(3).尾數部分(Mantissa):尾數部分
float的尾數位佔用23個二進位制位,double的尾數位佔用52二進位制位
5.圖形化參考方式:

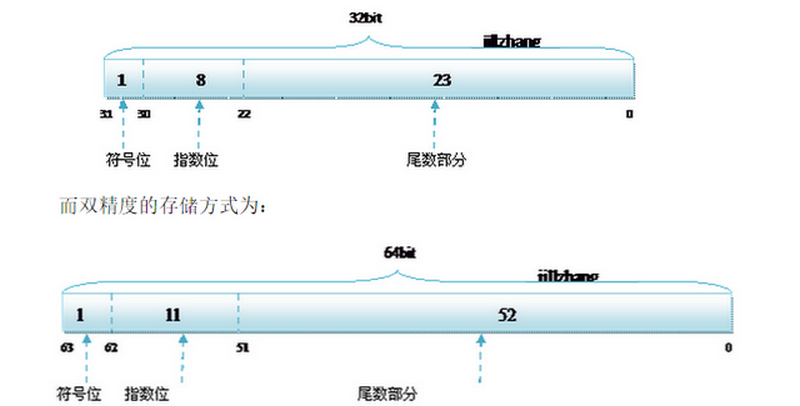
圖形化解釋:將一個float型別的浮點資料轉化為記憶體儲存格式的步驟詳解
(1).先將這個實數的絕對值轉化為規格化二進位制.
(2).將這個二進位制格式的實數的小數點左移或者右移n位,知道小數點移動到第一個有效數字的右邊.
(3).從小數點右邊第一位開始輸出23位數字放入二進位制位當中的第0~22位中(總共23位儲存尾數).
(4).如果實數是正的,則在第31位處的位置放入”0”,如果是負數則在31位處放置”1”.
(5).如果n是左移得到的,則將n減去1後化為二進位制,並在左邊加”0”,補足7位,放入到第29位到底23位之間,如果n是右移得到的貨n=0,則將n化為二進位制後在左邊加”0”補足7位,再個位進行求反,再放入到第
29位到底23位之間。
(6).第5個步驟還有另外一種解釋:
將其描述成為1.xxxx*2的n次方–>其中的n就是所謂的指數
再用最終的指數+127=階碼對應的十進位制資料–>轉化成為二進位制資料就行了–>放置到階碼位
如果是float+127,如果是double+1023得到階碼位(指數位)
6.額外補充內容:
R32.24和R64.53的儲存方式都是用科學計數法來儲存資料的,比如8.25用十進位制的科學計數法表示 就為:8.25×10^0,而120.5可以表示為1.205×10^2;而計算機根本不認識十進位制的資料,它只認識0和1,所以在計算機儲存中,首先要將上面的數更改為二進位制的科學計數法表示,8.25用二進位制表示可表示為1000.01,120.5用二進位制表示可表示為1110110.1;用二進位制的科學計數法表示1000.01可表示為1.00001×2^3,而1110110.1則可表示為1.1101101×2^6,任何一個數的科學計數法都可表示為1.xxx×2^n;因此尾數部分就可表示為xxx,反正第一位都是1,故可將小數點前面的1省略,故23bit的尾數部分,可以表達的精度卻變成了24bit,道理就是在這裡;那24bit能精確到小數點後的幾位呢?我們知道9的二進位制表示為1001,所以4bit能精確十進位制中的1位小數點,24bit就能使float能精確到小數點後6位;另算上可以估讀最後一位,故有效位數為7位.而對於指數部分,因為指數可正可負,8位的指數位能表示的指數範圍就應該為-127至128了,所以指數部分的儲存採用移位儲存,儲存的資料為原資料加127,下面就看看8.25和120.5在記憶體中真正的儲存方式.首先看下8.25,用二進位制的科學計數法表示1.00001×2^3。按照上面的儲存方式,符號位為0,表示為正;指數位為3+127=130(二進位制值10000010轉十進位制表示即為130);尾數部分為00001,故8.25的儲存方式如下圖所示:

120.5的儲存方式

二進位制轉浮點數
將一個記憶體儲存的float二進位制格式轉化為十進位制的步驟:
(1).將第22位到第0位的二進位制數寫出來,在最左邊補一位1,得到二十四位有效數字.將小數點點在最左邊那個1的右邊.
(2).取出第29到第23位所表示的值n,當30位是0時將n各位求反;當30位是1時將n增1.
(3).將小數點左移n位(當30位是0時)或右移n位(當30位是1時),得到一個二進位制表示的實數,
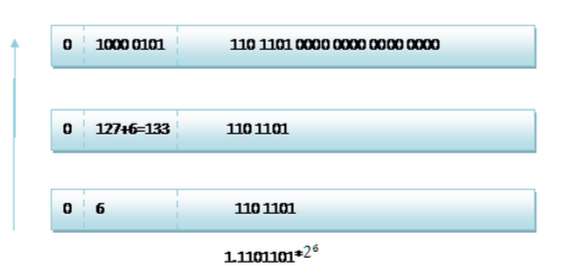
(4).將這個二進位制實數化為十進位制,並根據第31位是0還是1加上正號或負號即可.那麼如果給出記憶體中一段資料,並且告訴你是單精度儲存的話,你如何知道該資料的十進位制數值呢?其實就是對上面的反推過程,比如給出如下記憶體資料:0100001011101101000000000000,首先我們現將該資料分段,0 10000 0101 110 1101 0000 0000 0000 0000,在記憶體中的儲存就為下圖所示:

根據我們的計算方式,可以計算出,這樣一組資料表示為1.1101101*2^6=120.5
二雙精度浮點數(doube)的儲存和單精度的儲存大同小異,不同的只是階碼部分(指數部分)和尾數部分的位數不同而已,但是推導法則一模一樣,

對C語言中遞迴演算法的深入解析
C語言通過執行時堆疊支援遞迴函式的實現.遞迴函式就是直接或間接呼叫自身的函式.許多教科書都把計算機階乘和菲波那契數列用來說明遞迴,非常不幸我們可愛的著名的老潭老師的《C語言程式設計》一書中就是從階乘的計算開始的函式遞迴.導致讀過這本經書的同學們,看到階乘計算第一個想法就是遞迴.但是在階乘的計算裡,遞迴併沒有提供任何優越之處.在菲波那契數列中,它的效率更是低的非常恐怖.這裡有一個簡單的程式,可用於說明遞迴.程式的目的是把一個整數從二進位制形式轉換為可列印的字元形式.例如:給出一個值4267,我們需要依次產生字元’4’,’2’,’6’和’7’.就如在printf函式中使用了%d格式碼,它就會執行類似處理.我們採用的策略是把這個值反覆除以10,並列印各個餘數.例如,4267除10的餘數是7,但是我們不能直接列印這個餘數.我們需要列印的是機器字符集中表示數字’7’的值.在ASCII碼中,字元’7’的值是55,所以我們需要在餘數上加上48來獲得正確的字元,但是,使用字元常量而不是整型常量可以提高程式的可移植性.’0’的ASCII碼是48,所以我們用餘數加上’0’所以有下面的關係:
‘0’ + 0 = ‘0’;
‘0’ + 1 = ‘1’;
‘0’ + 2 = ‘2’;
……
從這些關係中,我們很容易看出在餘數上加上’0’就可以產生對應字元的程式碼.接著就列印出餘數.下一步再取商的值,4267/10等於426.然後用這個值重複上述步驟.這種處理方法存在的唯一問題是它產生的數字次序正好相反,它們是逆向列印的.所以在我們的程式中使用遞迴來修正這個問題.我們這個程式中的函式是遞迴性質的,因為它包含了一個對自身的呼叫.乍一看,函式似乎永遠不會終止.當函式呼叫時,它將呼叫自身,第2次呼叫還將呼叫自身,以此類推,似乎永遠呼叫下去.這也是我們在剛接觸遞迴時最想不明白的事情.但是,事實上並不會出現這種情況.這個程式的遞迴實現了某種型別的螺旋狀while迴圈.while迴圈在迴圈體每次執行時必須取得某種進展,逐步迫近迴圈終止條件.遞迴函式也是如此,它在每次遞迴呼叫後必須越來越接近某種限制條件.當遞迴函式符合這個限制條件時.它便不在呼叫自身.在程式中,遞迴函式的限制條件就是變quotient為零.在每次遞迴呼叫之前,我們都把quotient除以10,所以每遞迴呼叫一次,它的值就越來越接近零.當它最終變成零時,遞迴便告終止.
/接受一個整型值(無符號0,把它轉換為字元並列印它,前導零被刪除/

#include <stdio.h>
int binary_to_ascii( unsigned int value)
{
          unsigned int quotient;

   　　quotient = value / 10;
   　　if( quotient != 0)
       　　　　binary_to_ascii( quotient);
   　　putchar ( value % 10 + '0' );
}

遞迴是如何幫助我們以正確的順序列印這些字元呢?下面是這個函式的工作流程.
1.將引數值除以10.
2.如果quotient的值為非零,呼叫binary-to- ascii列印quotient當前值的各位數字
3.接著,列印步驟1中除法運算的餘數
注意:在第2個步驟中,我們需要列印的quotient當前值的各位數字.我們所面臨的問題和最初的問題完全相同,只是變數quotient的值變小了.我們用剛剛編寫的函式(把整數轉換為各個數字字元並列印出來)來解決這個問題.由於quotient的值越來越小,所以遞迴最終會終止.一旦你理解了遞迴,閱讀遞迴函式最容易的方法不是糾纏於它的執行過程,而是相信遞迴函式會順利完成它的任務.如果你的每個步驟正確無誤,你的限制條件設定正確,並且每次呼叫之後更接近限制條件,遞迴函式總是能正確的完成任務.但是,為了理解遞迴的工作原理,你需要追蹤遞迴呼叫的執行過程,所以讓我們來進行這項工作.追蹤一個遞迴函式的執行過程的關鍵是理解函式中所宣告的變數是如何儲存的.當函式被呼叫時,它的變數的空間是建立於執行時堆疊上的.以前呼叫的函式的變數扔保留在堆疊上,但他們被新函式的變數所掩蓋,因此是不能被訪問的.當遞迴函式呼叫自身時,情況於是如此.每進行一次新的呼叫,都將建立一批變數,他們將掩蓋遞迴函式前一次呼叫所建立的變數.當我追蹤一個遞迴函式的執行過程時,必須把分數不同次呼叫的變數區分開來,以避免混淆.程式中的函式有兩個變數:引數value和區域性變數quotient.下面的一些圖顯示了堆疊的狀態,當前可以訪問的變數位於棧頂,所有其他呼叫的變數飾以灰色的陰影,表示他們不能被當前正在執行的函式訪問.假定我們以4267這個值呼叫遞迴函式.當函式剛開始執行時,堆疊的內容如下圖所示:





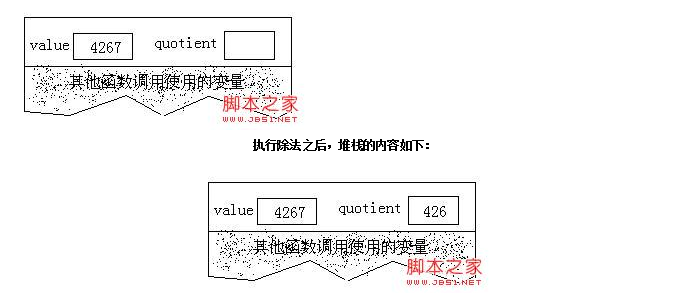
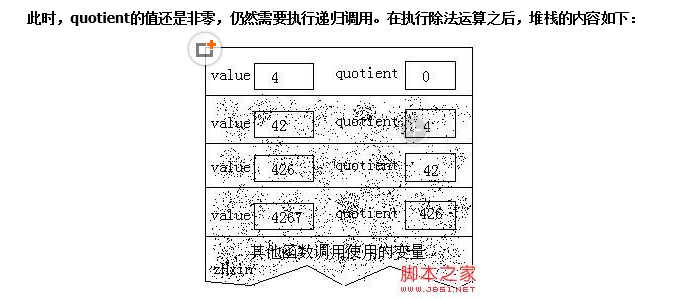
不算遞迴呼叫語句本身,到目前為止所執行的語句只是除法運算以及對quotient的值進行測試.由於遞迴呼叫這些語句重複執行,所以它的效果類似迴圈:當quotient的值非零時,把它的值作為初始值重新開始迴圈.但是,遞迴呼叫將會儲存一些資訊(這點與迴圈不同),也就好是儲存在堆疊中的變數值.這些資訊很快就會變得非常重要.現在quotient的值變成了零,遞迴函式便不再呼叫自身,而是開始列印輸出.然後函式返回,並開始銷燬堆疊上的變數值.每次呼叫putchar得到變數value的最後一個數字,方法是對value進行模10取餘運算,其結果是一個0到9之間的整數.把它與字元常量’0’相加,其結果便是對應於這個數字的ASCII字元,然後把這個字元列印出來.輸出4:



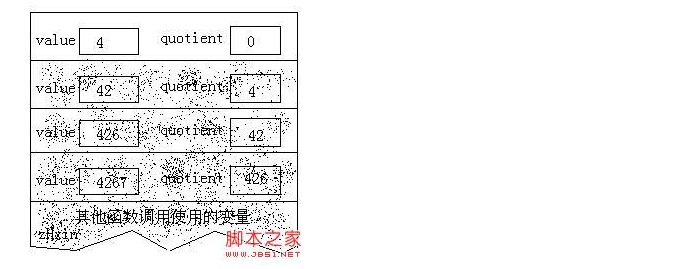
然後,這個遞迴函式就徹底返回到其他函式呼叫它的地點.如果你把列印出來的字元一個接一個排在一起,出現在印表機或螢幕上,你將看到正確的值:4267使用遞迴一定要有跳出的條件:這是一個最簡單的遞迴,不過它會一直執行,可用 Ctrl+C 終止.

#include <stdio.h>
void prn(int num) {
    printf("%d/n", num);
    if (num > 0) prn(--num);  
}
int main(void)
{
    prn(9);
    getchar();
    return 0;
}

//例項:翻轉字串
#include <stdio.h>
void revers(char *cs);
int main(void)
{
    revers("123456789");
    getchar();    
    return 0;
}
void revers(char *cs)
{
    if (*cs)
    { 
        revers(cs + 1);
        putchar(*cs);
    }
}

//例項:階乘
#include <stdio.h>
int factorial(int num);
int main(void)
{
    int i;
    for (i = 1; i <= 9; i++)
    printf("%d: %d/n", i, factorial(i));
    getchar();    
    return 0;
}
int factorial(int num)
{
    if (num == 1)
        return(1);
    else
        return(num * factorial(num-1));
}

//例項:整數到二進位制
#include <stdio.h>
void IntToBinary(unsigned num);
int main(void)
{
    IntToBinary(255); /* 11111111 */
    getchar();
    return 0;
}
void IntToBinary(unsigned num) {
    int i = num % 2;
    if (num > 1) IntToBinary(num / 2);
    putchar(i ? '1' : '0'); 
//    putchar('0' + i);  /* 可代替上面一句 */
}

//剖析遞迴:
#include <stdio.h>
void prn(unsigned n);
int main(void)
{
    prn(1);
    getchar();
    return 0;
}
void prn(unsigned n) {
    printf("%d: %p/n", n, &n);  /* A */
    if (n < 4) 
        prn(n+1);               /* B */
    printf("%d: %p/n", n, &n);  /* C */
}

分析:
程式執行到A,輸出了第一行.
此時n=1,滿足<4的條件,繼續執行B開始了自呼叫(接著會輸出第二行);注意n=1時語句C還有待執行.
……如此迴圈,一直到n=4,A可以執行,但因不滿足條件B執行不了了;終於在n=4時得以執行C.但此時記憶體中有四個函式都等待返回(分別是n=1,2,3,4時), 我們們分別叫它f1,f2,f3,f4.f4執行C輸出了第五行,函式返回,返回給f3(此時n=3),f3得以繼續執行C,輸出了第六行.
f3–>f2–>繼續C,輸出了第七行.
f2–>f1–>繼續C,輸出了第八行, 執行完畢!
如此看來,遞迴函式還是很費記憶體的(有時不如直接使用迴圈),但的確很巧妙.