A*演算法圖解

記得好象剛知道遊戲開發這一行的時候老師就提到過A星演算法,當時自己基礎還不行,也就沒有去看這方面的資料,前幾天找了一些資料,研究了一天,覺的現在網上介紹A星演算法的資料都講的不夠詳細(因為我下的那個資料基本算是最詳細的了- -但是都有一些很重要的部分沒有說清楚….),所以我自己重新寫一篇講解A星演算法的資料,還是借用其他資料的一些資源.不過轉載太多了,只有謝謝原作者了:) 我們將以下圖作為地圖來進行講解,圖中對每一個方格都進行了編號,其中綠色的方格代表起點,紅色的方格代表終點,藍色的方格代表障礙,我們將用A星演算法來尋找一條從起點到終點最優路徑,為了方便講解,我們規定只能走上下左右4個方向,當你理解了A星演算法,8個方向也自然明白。

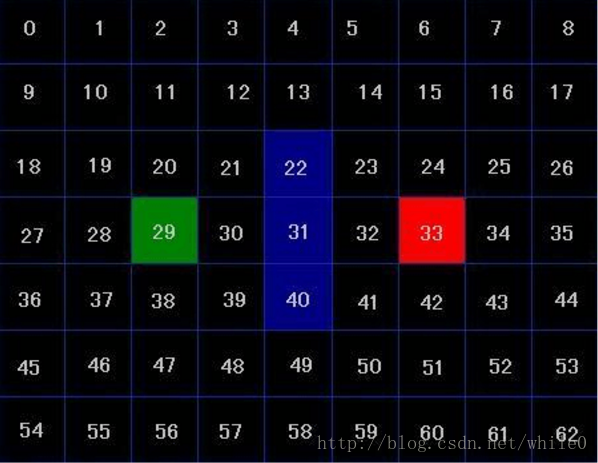
在地圖中,每一個方格最基本也要具有兩個屬性值,一個是方格是通暢的還是障礙,另一個就是指向他父親方格的指標，父親方格也就是路徑中上一個經過的方格 (相當於雙向連結串列結構中的父結點指標), 我們假設方格值為0時為通暢,值為1時為障礙。A星演算法中,有2個相當重要的元素,第一個就是指向父親結點的指標,第二個就是一個OPEN表,第三個就是CLOSE表,這兩張表的具體作用我們在後面邊用邊介紹,第四個就是每個結點的F值(F值相當於圖結構中的權值) 而F = H + G;其中H值為從網格上當前方格移動到終點的預估移動耗費。這經常被稱為啟發式的，可能會讓你有點迷惑。這樣叫的原因是因為它只是個猜測。我們沒辦法事先知道路徑的長度，因為路上可能存在各種障礙(牆，水，等等)。雖然本文只提供了一種計算H的方法，但是你可以在網上找到很多其他的方法,我們定義H值為：終點所在行減去當前格所在行的絕對值與終點所在列減去當前格所在列的絕對值 之和,而G值為從當前格的父親格移動到當前格的預估移動耗費,在這裡我們設定一個基數10,每個H和G都要乘以10,這樣方便觀察 好了,我們開始對地圖進行搜尋 首先,我們將起點的父親結點設定為NULL,然後將起點的G值設定為0,再裝進open表裡面,然後將起點作為父親結點的周圍4個點20,28,30,38(因為我們地圖只能走4個方向,如果是8方向,則要再加4個點進去)都加進open列表裡面,並算去每個結點的H值,然後再將起點從open列表刪除,放進close表中,我們將放進close表的所有方格都用淺藍色線條進行框邊處理,所以這次搜尋以後,圖片變為如下格式,其中箭頭代表的是其父結點

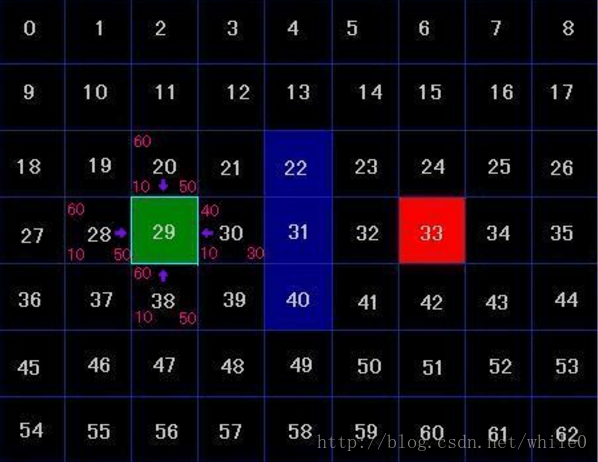
其中每個格子的左下方為G值,右下方為H值,左上方為F值,我們拿28號格子為例來講解一寫F值的演算法,首先因為終點33在4行7列,而28在4行2列,則行數相差為0,列數相差為5,總和為5,再乘以我們先前定的基數10,所以H值為50,又因為從28的父結點29移動到28,長度為1格,而29號為起點，G值為0,所以在父親結點29的基礎上移動到28所消耗的G值為(0 + 1) *10 = 10,0為父親結點的G值,1為從29到28的消耗 當前OPEN表中的值: 20,28,30,38 當前CLOSE表中的值: 29 現在我們開始尋找OPEN列表中F值最低的,得出結點30的F值最低,且為40,然後將結點30從OPEN表中刪除,然後再加入到CLOSE表中,然後在判斷結點30周圍4個結點,因為結點31為障礙,結點29存在於CLOSE表中,我們將不處理這兩點,只將21和39號結點加入OPEN表中,新增完後地圖變為下圖樣式 當前OPEN表中的值: 20,28,38,21,39 當前CLOSE表中的值: 29,30

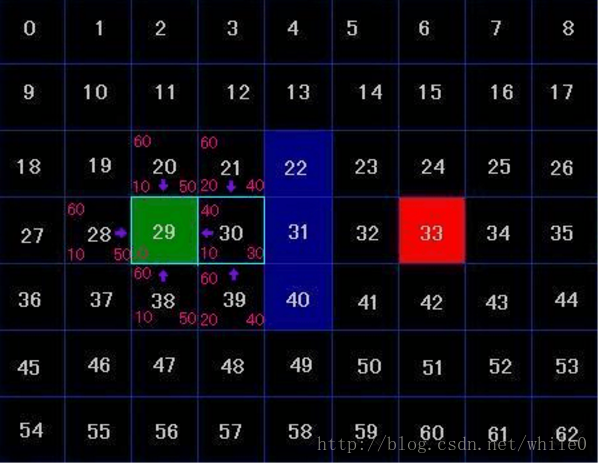
接著我們重複上面的過程,尋找OPEN表中F值為低的值,我們發現OPEN表中所有結點的F值都為60,我們隨即取一個結點,這裡我們直接取最後新增進OPEN表中的結點,這樣方便訪問(因為存在這樣的情況,所有從一個點到另外一個點的最短路徑可能不只一條),我們取結點39,將他從OPEN表中刪除,並新增進CLOSE表中,然後觀察39號結點周圍的4個結點,因為40號結點為障礙,所以我們不管它,而30號結點已經存在與OPEN表中了,所以我們要比較下假設39號結點為30號結點的父結點,30號結點的G值會不會更小,如果更小的話我們將30結點的父結點改為39號,這裡我們以39號結點為父結點,得出30號結點的新G值為30,而30號結點原來的G值為10,並不比原來的小,所以我們不對30號進行任何操作,同樣的對38號結點進行上述操作後我們也不對它進行任何操作,接著我們把48號結點新增進OPEN表中,新增完後地圖變為下圖樣式 當前OPEN表中的值: 20,28,38,21,48 當前CLOSE表中的值: 29,30,39

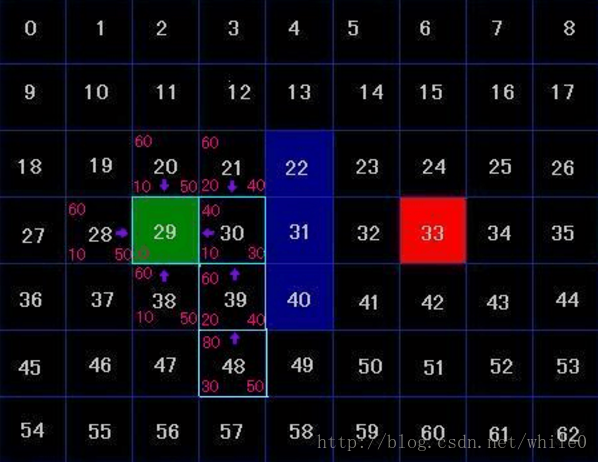
以後的過程中我們都重複這樣的過程,一直到遍歷到了最後終點,通過遍歷父結點編號,我們能夠得出一條最短路徑,具體完整的推導過程我就不寫出來了,因為和剛才那幾步是一樣的，這裡我再講出一個特例,然後基本A星演算法就沒問題了 上面的最後一推導中,我們在觀察39號結點時,發現他周圍已經有結點在OPEN表中了,我說”比較下假設39號結點為30號結點的父結點,30號結點的G值會不會更小,如果更小的話我們將30結點的父結點改為39號”,但是剛才沒有遇到G值更小的情況，所以這裡我假設出一種G值更小的情況,然後讓大家知道該怎麼操作,假設以39號為父結點,我們得出的30號的新G值為5(只是假設),比30號的原G值10還要小,所以我們要修改路徑,改變30號的箭頭,本來他是指向29號結點的，我們現在讓他指向39號結點。
好了,A星演算法的大體思路就是這樣了，對於8方向的地圖來說，唯一的改變就是G值方面,在上下左右,我們的G值是加10,但是在斜方向我們要加14,其他的和上面講的一樣~~~:)