轉載請註明出處：http://blog.csdn.net/ns_code/article/details/20478753

前言

    最後三種排序演算法了，由於都不是基於比較的排序，因此這三種排序演算法可以以線性時間執行。但是因為限制條件的特殊性，因此應用面沒有基於元素比較的排序演算法廣，但是在很多特定的情況下還是蠻有用途的，而且效率極高。

計數排序

    計數排序是建立在這樣的前提條件下的：假設n個輸入元素的每一個都是0到k區間內的一個整數，其中k為某個整數。因此我們後面所寫的程式也只是針對0到k之間的元素進行排序，換句話說，排序元素中不能有負數。

    計數排序的基本思想是：對一個輸入元素x，先確定所有輸入元素中小於x的元素個數，那麼排序後x所在的位置也就明確了。比如，所有的輸入元素中有10個元素小於x，那麼排好序後x的位置序號就應該是11。當然，如果有相同元素，自然要放到相鄰的位置上。

    演算法導論上給出了計數排序的很詳細的虛擬碼，我們根據此虛擬碼，並設陣列arr為輸入陣列，arr中的每個元素值在0到k之間，brr為排序後的輸出陣列，crr記錄arr中每個元素出現的次數。寫出程式碼如下：

/*
第一種形式實現計數排序
計數排序後的順序為從小到大
arr[0...len-1]為待排陣列，每個元素均是0-k中的一個值
brr[0...len-1]為排序後的輸出陣列
crr[0...k]儲存0...k中每個值在陣列arr中出現的次數
*/
void Count_Sort(int *arr,int *brr,int *crr,int len,int k)
{
	int i,j=0;
	//陣列crr各元素置0
	for(i=0;i<=k;i++)
		crr[i] = 0;
	//統計陣列arr中每個元素重複出現的個數
	for(i=0;i<len;i++)
		crr[arr[i]]++;
	//求陣列arr中小於等於i的元素個數
	for(i=1;i<=k;i++)
		crr[i] += crr[i-1];
	//把arr中的元素放在brr中對應的位置上
	for(i=len-1;i>=0;i--)
	{
		brr[crr[arr[i]]-1] = arr[i];
		//如果有相同的元素，則放在下一個位置上
		crr[arr[i]]--;
	}
}

    很明顯上面程式碼的時間複雜度為O（n+k），但用到了brr來儲存排序結果，我們可以它做些改進，使排序原地進行，如下：

/*
第二種形式實現計數排序
計數排序後的順序為從小到大
arr[0...len-1]為待排陣列，每個元素均是0-k中的一個值
crr[0...k]儲存0...k中每個值在陣列arr中出現的次數
*/
void Count_Sort(int *arr,int *crr,int len,int k)
{
	int i,j=0;
	//陣列crr各元素置0
	for(i=0;i<=k;i++)
		crr[i] = 0;
	//統計陣列arr中每個元素重複出現的個數
	for(i=0;i<len;i++)
		crr[arr[i]]++;
	//根據crr[i]的大小，將元素i放入arr適當的位置
	for(i=0;i<=k;i++)
		while((crr[i]--)>0)
		{
			arr[j++] = i;
		}
}

    採用如下程式碼測試：

int main()
{
	int i; 
	//待排序陣列，每個元素均在0-8之間
	int arr[] = {2,1,3,8,6,0};
	int brr[6];
	int crr[9];
	Count_Sort(arr,brr,crr,6,8);
	printf("計數排序後的結果為：");
	for(i=0;i<6;i++)
		printf("%d ",brr[i]);
	printf("\n");
	return 0;
}

    測試結果如下：

    最後我們稍微總結下計數排序的特點：

    1、不是基於比較的排序，因此可以達到線性排序時間；

    2、採取空間換時間的思想，需要brr和crr等輔助空間，但是時間複雜度僅為O（n+k）；

    3、穩定性好，這也是計數排序最重要的一個特性。

    在實際工作中，當k=O（n）時，我們一般才會採取計數排序，如果k很大，則不宜採取該演算法，尤其在如下情形下：

待排序元素為：1、3、8、5、10000000，這樣會造成很大的資源浪費。

基數排序

    基數排序的排序時間也可以達到線性，尤其在k和d（後面介紹該引數）很小的情況下。

    基數排序採取的是多關鍵字比較的策略，且每個關鍵字對排序的影響不同，根據關鍵字影響的主次，有兩種排序方法：

    1、先根據影響最大的關鍵字來排序，而後在該關鍵字相同的情況下，再根據影響次之的關鍵字來排序，依此類推，直到最後按照影響最小的關鍵字排序後，序列有序。我們稱這個為先高位後低位。

    2、先根據影響最小的關鍵字來排序，而後再對全部的元素根據影響次小的關鍵字來排序，依此類推，直到最後按照影響最大的關鍵字排序後，序列有序。我們稱這個為先低位後高位。

    這有點抽象，我們用具體的例子來說明。比如，我們希望用三個關鍵字（年、月、日）來對日期進行排序，按照基數排序的思想，則：

    採取第一種方法排序的思路是這樣的：先比較年，形成一個按照年有序排列的序列，而後對年相等的日期，在比較月，對月相等的日期，再比較日，最後得到有序序列。

    採取第二種方法排序的思路是這樣的：先對所有元素按照日排序，再對所有元素按照月排序，最後對所有元素按照年排序，得到有序序列。

    我們一般採用第二種方法來進行排序，比如如下的數字序列：

217，125，362，136，733，522

    先對個位上的數字進行排序，得到：

362，522，733，125，136，217

    再對十位上的數字進行排序，得到：

217，522，125，733，136，362

    最後對百位上的數字進行排序，得到：

125，136，217，362，522，733

    很明顯，高位數字比低位數字對排序的影響大，該方法的正確性很容易證明，這裡不再說明。

    我們注意到，這裡每一步都需要對各個位上的數進行排序。而為了保證基數排序的正確性（穩定性），我們對每個位上的數進行排序時可以選用計數排序。演算法導論上給的虛擬碼太粗略了，直接貼出自己寫的完全程式碼（包括測試程式碼），如下：

/*******************************
		  基數排序
Author:蘭亭風雨 Date:2014-03-03
Email:zyb_maodun@163.com
********************************/
#include<stdio.h>
#include<stdlib.h>

/*
在第一種計數排序的實現形式上做了些修改
計數排序後的順序為從小到大
arr[0...len-1]為待排陣列，我們這裡採用三位數
brr[0...len-1]為排序後的有序陣列
w[0...len-1]用來儲存取出的每一位上的數，其每個元素均是0-k中的一個值
crr[0...k]儲存0...k中每個值出現的次數
*/
void Count_Sort(int *arr,int *brr,int *w,int *crr,int len,int k)
{
	int i;
	//陣列crr各元素置0
	for(i=0;i<=k;i++)
		crr[i] = 0;
	//統計陣列w中每個元素重複出現的個數
	for(i=0;i<len;i++)
		crr[w[i]]++;
	//求陣列w中小於等於i的元素個數
	for(i=1;i<=k;i++)
		crr[i] += crr[i-1];
	//把arr中的元素放在brr中對應的位置上
	for(i=len-1;i>=0;i--)
	{
		brr[crr[w[i]]-1] = arr[i];
		//如果有相同的元素，則放在下一個位置上
		crr[w[i]]--;
	}
	//再將brr中的元素複製給arr，這樣arr就有序了
	for(i=0;i<len;i++)
	{
		arr[i] = brr[i];
	}
}

/*
基數排序後的順序為從小到大
其中引數d為元素的位數
*/
void Basic_Sort(int *arr,int *brr,int *w,int *crr,int len,int k,int d)
{
	int i,j,val=1;
	//從低位到高位依次進行計數排序
	for(i=1;i<=d;i++)
	{	//w中儲存的是arr中每個元素對應位上的數
		//範圍在0-k之間
		for(j=0;j<len;j++)
			w[j] = (arr[j]/val)%10;	
		//對當前位進行計數排序
		Count_Sort(arr,brr,w,crr,len,k);
		val *= 10;
	}
}

int main()
{
	int i; 
	//待排序陣列，每個元素的每一位均在0-7之間
	int arr[] = {217,125,362,136,733,522};
	int brr[6];	//用來儲存每次計數排序後的結果
	int w[6];	//每次迴圈時，儲存該位上的數
	int crr[8];	//每次迴圈時，儲存該位上的數出現的次數
	Basic_Sort(arr,brr,w,crr,6,7,3);
	printf("計數排序後的結果為：");
	for(i=0;i<6;i++)
		printf("%d ",arr[i]);
	printf("\n");
	return 0;
}

    測試結果如下：

    1、同樣不是基於比較的排序，因此可以達到線性排序時間；

    2、同樣採取空間換時間的思想，需要額外的輔助空間，但是時間複雜度僅為O（d(n+k)）；

    3、基數排序的穩定性同樣也很好。

    吐槽一下：寫Basic_Sort的時候，每一次的val應該是10的i-1次方，手誤，打成了10*（i-1）， 跟蹤除錯了一下午，每次迴圈w陣列中的值都是個位數，就在那幾行程式碼找問題，但尼瑪我偏偏就是沒看出來。

桶排序

    桶排序假設輸入資料服從均勻分佈，平均情況下它的時間複雜度為O（n）。與計數排序類似，因為對輸入資料作了某種假設，桶排序的速度也很快。

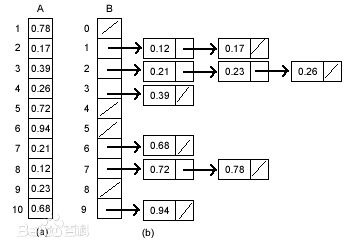
    桶排序將輸入元素按照一定的區間劃分為若干個桶，因為假設了輸入的資料在總的區間範圍內是均勻分佈的，因此一般不會出現很多個元素落在同一個桶中的情況。我們可以先對每個桶中的元素排序，而後按照桶的序號，依次把各個桶中的元素列出來即可。

    在進行桶排序時，我們需要一個輔助陣列來存放每個桶，而每個桶中的元素最好用連結串列串起來，這樣操作起來比較方便。一個很普遍的展示圖例如下：

    桶排序瞭解思想即可，程式碼我們就不再實現了，因為它的實現不具備普遍性，要根據不同的情況來劃分不同個數的桶，以及桶所規定的區間。

    2014校招時創新工廠下的塗鴉移動有一道這樣的面試題：

    一個字元陣列，裡面的字元可能是a-z、A-Z、0-9.現在要求對陣列進行排序，要求所有小寫字元放在最前面，所有大寫字元放在中間，所有數字放在最後。而且各部分內部分別有序。

    這個很明顯用桶排序來實現效果最佳，尤其在資料量非常大的情況下。

再比如，如下情況也是用桶排序的最佳時機（摘自百度百科）

海量資料