【資料結構與演算法】二叉排序樹C實現（含完整原始碼）

蘭亭風雨發表於2014-02-25
資料結構演算法排序原始碼

轉載請註明出處：http://blog.csdn.net/ns_code/article/details/19823463


二叉排序樹簡介 

    二叉排序樹（Binary Sort Tree，簡稱BST），又稱二叉查詢樹，是紅黑樹、AVL樹等的基礎。它或是一棵空樹，或者是具有下列性質的一棵二叉樹：

   1、若它的左子樹不空，則左子樹上所有節點的值均小於它的根節點的值；

   2、若它的右子樹不空，則右子樹上所有節點的值均大於它的根節點的值；

   3、它的左右子樹也分別為二叉排序樹。

   下面的一棵樹即為二叉排序樹：

  

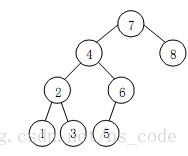
    很明顯，對二叉排序樹進行中序遍歷，便可得到一個有序序列，該有序序列中的各元素按照從小到大的順序排列，因此一個無序序列可以通過構造一棵二叉排序樹而變成一個有序序列。


二叉排序樹相關操作

    二叉排序樹通常有查詢、插入、刪除等操作。查詢操作很簡單，無非就是遞迴查詢，有點類似二叉樹遍歷的過程。插入操作也不難，一般是先在二叉排序樹pTree中查詢，看是否存在有等於給定值的元素，如果查詢不到，則將給定值插入到該二叉排序樹中，但是要保證插入後的樹依然是二叉排序樹。這樣，新節點插入的位置便是唯一的，而且新插入的節點一定是一個新新增的葉子節點，並且是查詢不成功時查詢路徑上訪問的最後一個節點的左孩子或右孩子。正是由於其在查詢過程中插入節點的特性，二叉排序樹是一種動態樹。

    在給出各操作實現的具體程式碼前，要詳細看下二叉排序樹的刪除操作，刪除操作相比於二叉排序樹的其他操作要難些，但也只是相對於其本身的其他操作而已，真正理解了也就很容易了。閒話少說，下面就來具體分析二叉排序樹的刪除操作。

    我們假設在二叉排序樹中要被刪除的節點為p（即p指向的節點，下同），其父節點為f，當然節點p可能是節點f的的左孩子或右孩子，但在下面各種情況的分析中，你會發現，無論是左孩子還是右孩子，都不影響刪除操作的通用性。很明顯，刪除操作要分為如下3種情況：

    1、若待刪節點p為葉子節點，則刪除p後，並不會破壞整棵樹的結構，因此只需令p=NULL即可。

    2、若待刪節點p只有左子樹或右子樹，則只需將左子樹或右子樹重接到p的父節點上即可，即執行如下操作：p=p->lchild或p=p->rchild。

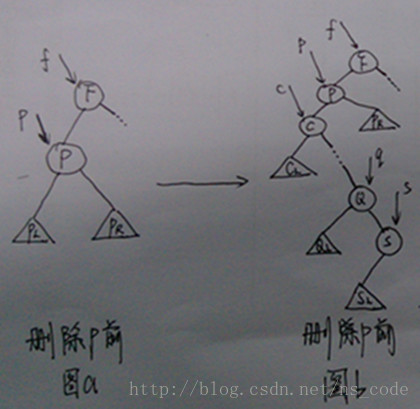
    3、若待刪節點p既有左子樹又有右子樹，顯然就不如上面兩種情況那麼簡單了。我們要使節點p被刪除後，二叉排序樹的結構不變，就需要對它的子樹做一些操作，而且只需操作一個子樹即可，操作左子樹和操作右子樹的思路相似，我們這裡以操作左子樹為例來實現節點p的刪除操作，並結合下圖做具體分析（圖中三角形代表節點的左子樹或右子樹）。


    我們這裡將圖a展開為更詳細的圖b進行分析，則在刪除節點p前，中序遍歷該二叉排序樹的結果為：...CL C...QL Q SL S P PR F ...，刪除節點p後，我們要保持其他元素在該序列中的先後順序不變，觀察圖b，我們可以採取如下兩種做法：

    1）將節點p的左子樹直接接到其父節點f上，作為f的左子樹，將節點p的右子樹接到節點s上，作為s的右子樹（這裡s為p的前驅節點，即p在有序序列中緊接在s的前面），而後刪除節點p。採用這種方法刪除節點p後，得到的二叉排序樹的形狀如下圖中的圖c所示：


    採取該方法刪除節點的實現程式碼如下：

/*
採用第一種演算法從二叉排序樹中刪除指標p所指向的節點,
並在保持二叉排序樹有序的情況下，將其左右子樹重接到該二叉排序樹中.
該函式主要用來被後面的刪除函式呼叫
*/
void delete_Node1(BSTree &p)
{ 
	BSTree q,s;
	if(!p->lchild)	
	{	//如果左子樹為空，則只需重接其右子樹
		//這裡包含了左右子樹均為空的情況
		q = p;
		p = p->rchild ;
		free(q);
	}
	else if(!p->rchild)
	{	//如果右子樹為空，則只需重接其左子樹
		q = p;
		p = p->lchild;
		free(q);
	}
	else
	{	//如果左右子樹都不為空，我們採取第一種方法來重接左右子樹，
		//我們這裡採取修改左子樹的方法，也可以修改右子樹，方法類似
		s = p->lchild;		//取待刪節點的左節點

		//一直向右，最終s為待刪節點的前驅節點
		//如果將各節點元素按從小到大順序排列成一個序列，
		//則某節點的前驅節點即為序列中該節點的前面一個節點
		while(s->rchild)
			s = s->rchild;
		s->rchild = p->rchild;	//將p的右子樹接為s的右子樹
		q = p;
		p = p->lchild;		//將p的左子樹直接接到其父節點的左子樹上
		free(q);
	}
}
    2）將節點s的右子樹重接到其父節點上，作為其父節點的右子樹，而後用s替換掉帶刪節點p。採取這種方法刪除節點p後，得到的二叉排序樹的形狀如上圖中的圖d所示。採用該方法刪除節點的實現程式碼如下：

/*
採用第二種演算法從二叉排序樹中刪除指標p所指向的節點,
並在保持二叉排序樹有序的情況下，將其左右子樹重接到該二叉排序樹中.
該函式主要用來被後面的刪除函式呼叫
*/
void delete_Node2(BSTree &p)
{
	BSTree q,s;		
	if(!p->lchild)	
	{	//如果左子樹為空，則只需重接其右子樹
		//這裡包含了左右子樹均為空的情況
		q = p;
		p = p->rchild ;
		free(q);
	}
	else if(!p->rchild)
	{	//如果右子樹為空，則只需重接其左子樹
		q = p;
		p = p->lchild;
		free(q);
	}
	else
	{	//如果左右子樹都不為空，我們採取第二種方法來重接左右子樹，
		//我們這裡採取修改左子樹的方法，也可以修改右子樹，方法類似
		q = p;
		s = p->lchild;		//取待刪節點的左節點
		while(s->rchild)		
		{	//一直向右，最終s為待刪節點的前驅節點。
			//如果將各節點元素按從小到大順序排列成一個序列，
			//則某節點的前驅節點即為序列中該節點的前面一個節點
			q = s;
			s = s->rchild;
		}
		//用s來替換待刪節點p
		p->data = s->data;  
		//根據情況，將s的左子樹重接到q上
		if(p != q)
			q->rchild = s->lchild;
		else
			q->lchild =s->lchild;
		free(s);
	}
}
 

完整原始碼

    上面重點分析了刪除節點的思路和過程，下面給出二叉排序樹各種操作實現的完整C程式碼（含測試程式碼並加有詳細註釋）：

/*********************************
二叉排序樹的相關操作實現
Author:蘭亭風雨  Date：2014-02-23
Email:zyb_maodun@163.com
**********************************/
#include<stdio.h>
#include<stdlib.h>

typedef struct Node
{
	int data;
	struct Node *lchild;
	struct Node *rchild;
}NODE,*BSTree;


/*
在指標pTree所指的二叉排序樹中遞迴查詢關鍵字為key的元素，
若查詢成功，則返回指向該元素節點的指標，否則返回NULL
*/
BSTree search(BSTree pTree,int key)
{
	if(!pTree || pTree->data == key)	//查詢到時返回的pTree為該元素節點，沒查詢到時為NULL
		return pTree;
	else if(key < pTree->data)			//如果key小於當前節點的值，則在其左子樹中遞迴查詢
		return search(pTree->lchild,key);
	else								//如果key大於當前節點的值，則在其右子樹中遞迴查詢
		return search(pTree->rchild,key);
}


/*
在指標pTree所指的二叉排序樹中遞迴查詢關鍵字為key的元素，
若查詢成功，則返回ture，並查詢到的資料對應的節點指標儲存在p中，
否則返回false，並將查詢路徑上訪問的最後一個節點指標儲存在p中。
這裡的引數parent指向每次遞迴遍歷的子樹的根節點的父節點，即始終是引數pTree的父節點，
它的初始值為NULL，其目的是跟蹤查詢路徑上訪問的當前節點的父節點（即上一個訪問節點）
該函式用來被後面的插入函式呼叫。
*/
bool search_BSTree(BSTree pTree,int key,BSTree parent,BSTree &p)
{
	if(!pTree)         //如果pTree為NULL，則查詢不成功												
	{	//這裡包含了樹空，即pTree為NULL的情況
		p = parent;
		return false;
	}
	else             //否則，繼續查詢
	{								
		if(key == pTree->data)			//如果相等，則查詢成功					
		{
			p = pTree;
			return true;
		}
		else if(key < pTree->data)		//在左子樹中遞迴查詢
			return search_BSTree(pTree->lchild,key,pTree,p);    
		else							//在右子樹中遞迴查詢
			return search_BSTree(pTree->rchild,key,pTree,p);
    }
}

/*
當在pTree所指向的二叉排序樹中查詢不到關鍵字為key的資料元素時，
將其插入該二叉排序樹，並返回ture，否則返回false。
樹空時插入會改變根節點的值，因此要傳入引用。
*/
bool insert(BSTree &pTree,int key)
{
	BSTree p;
	if(!search_BSTree(pTree,key,NULL,p))		//如果查詢失敗，則執行插入操作
	{
		//為新節點分配空間，並對各域賦值
		BSTree pNew = (BSTree)malloc(sizeof(NODE));
		pNew->data = key;
		pNew->lchild = pNew->rchild = NULL;

		if(!p)						    //如果樹空，則直接置pNew為根節點
			pTree = pNew;
		else if(key < p->data)			//作為左孩子插入p的左邊
			p->lchild = pNew;	        //作為右孩子插入p的右邊	
		else
			p->rchild = pNew;
		return true;
	}
	else
		return false;
}

/*
採用第一種演算法從二叉排序樹中刪除指標p所指向的節點,
並在保持二叉排序樹有序的情況下，將其左右子樹重接到該二叉排序樹中.
該函式主要用來被後面的刪除函式呼叫
*/
void delete_Node1(BSTree &p)
{ 
	BSTree q,s;
	if(!p->lchild)	
	{	//如果左子樹為空，則只需重接其右子樹
		//這裡包含了左右子樹均為空的情況
		q = p;
		p = p->rchild ;
		free(q);
	}
	else if(!p->rchild)
	{	//如果右子樹為空，則只需重接其左子樹
		q = p;
		p = p->lchild;
		free(q);
	}
	else
	{	//如果左右子樹都不為空，我們採取第一種方法來重接左右子樹，
		//我們這裡採取修改左子樹的方法，也可以修改右子樹，方法類似
		s = p->lchild;		//取待刪節點的左節點

		//一直向右，最終s為待刪節點的前驅節點
		//如果將各節點元素按從小到大順序排列成一個序列，
		//則某節點的前驅節點即為序列中該節點的前面一個節點
		while(s->rchild)
			s = s->rchild;
		s->rchild = p->rchild;	//將p的右子樹接為s的右子樹
		q = p;
		p = p->lchild;		//將p的左子樹直接接到其父節點的左子樹上
		free(q);
	}
}

/*
採用第二種演算法從二叉排序樹中刪除指標p所指向的節點,
並在保持二叉排序樹有序的情況下，將其左右子樹重接到該二叉排序樹中.
該函式主要用來被後面的刪除函式呼叫
*/
void delete_Node2(BSTree &p)
{
	BSTree q,s;		
	if(!p->lchild)	
	{	//如果左子樹為空，則只需重接其右子樹
		//這裡包含了左右子樹均為空的情況
		q = p;
		p = p->rchild ;
		free(q);
	}
	else if(!p->rchild)
	{	//如果右子樹為空，則只需重接其左子樹
		q = p;
		p = p->lchild;
		free(q);
	}
	else
	{	//如果左右子樹都不為空，我們採取第二種方法來重接左右子樹，
		//我們這裡採取修改左子樹的方法，也可以修改右子樹，方法類似
		q = p;
		s = p->lchild;		//取待刪節點的左節點
		while(s->rchild)		
		{	//一直向右，最終s為待刪節點的前驅節點。
			//如果將各節點元素按從小到大順序排列成一個序列，
			//則某節點的前驅節點即為序列中該節點的前面一個節點
			q = s;
			s = s->rchild;
		}
		//用s來替換待刪節點p
		p->data = s->data;  
		//根據情況，將s的左子樹重接到q上
		if(p != q)
			q->rchild = s->lchild;
		else
			q->lchild =s->lchild;
		free(s);
	}
}

/*
若pTree所指向的二叉排序樹中查詢到關鍵字為key的資料元素，
則刪除該元素對應的節點，並返回true，否則返回false
如果要刪除的恰好是根節點，則會改變根節點的值，因此要傳入引用
*/
bool delete_BSTree(BSTree &pTree,int key)
{
	//不存在關鍵字為key的節點
	if(!pTree)
		return false;
	else
	{	
		if(key == pTree->data)       //查詢到關鍵字為key的節點
		{
			delete_Node1(pTree);
//			delete_Node2(pTree);
			return true;			
		}
		else if(key < pTree->data)  //繼續查詢左子樹
			return delete_BSTree(pTree->lchild,key);
		else                        //繼續查詢右子樹
			return delete_BSTree(pTree->rchild,key);
	}
}

/*
根據所給的長為len的arr陣列，按陣列中元素的順序構建一棵二叉排序樹
*/
BSTree create_BSTree(int *arr,int len)
{
	BSTree pTree = NULL;
	int i;
	//按順序逐個節點插入到二叉排序樹中
	for(i=0;i<len;i++)
		insert(pTree,arr[i]);
	return pTree;	
}

/*
遞迴中序遍歷二叉排序樹，得到元素從小到大有序排列的序列
*/
void in_traverse(BSTree pTree)
{
	if(pTree)
	{
		if(pTree->lchild)
			in_traverse(pTree->lchild);
		printf("%d ",pTree->data);
		if(pTree->rchild)
			in_traverse(pTree->rchild);	
	}
}

/*
遞迴銷燬二叉排序樹
*/
void destroy_BSTree(BSTree pTree)
{
	if(pTree)
	{
		if(pTree->lchild)
			destroy_BSTree(pTree->lchild);
		if(pTree->rchild)
			destroy_BSTree(pTree->rchild);
		free(pTree);
		pTree = NULL;
	}
}

int main()
{
	int i;
	int num;
	printf("請輸入節點個數：");
	scanf("%d",&num);

	//輸入num個整數
	int *arr = (int *)malloc(num*sizeof(int));
	printf("請依次輸入這%d個整數（必須互不相等）：",num);
	for(i=0;i<num;i++)
		scanf("%d",arr+i);

	//中序遍歷該二叉排序樹，使資料按照從小到大的順序輸出
	BSTree pTree = create_BSTree(arr,num);
	printf("中序遍歷該二叉排序樹的結果：");
	in_traverse(pTree);
	printf("\n");

	//查詢給定的整數
	int key;
	printf("請輸入要查詢的整數：");
	scanf("%d",&key);
	if(search(pTree,key))
		printf("查詢成功\n");
	else 
		printf("查詢不到該整數\n");

	//插入給定的整數
	printf("請輸入要插入的整數：");
	scanf("%d",&key);
	if(insert(pTree,key))
	{
		printf("插入成功，插入後的中序遍歷結果：");
		in_traverse(pTree);
		printf("\n");
	}
	else
		printf("插入失敗，該二叉排序樹中已經存在整數%d\n",key);

	//刪除給定的整數
	printf("請輸入要刪除的整數：");
	scanf("%d",&key);
	if(delete_BSTree(pTree,key))
	{
		printf("刪除成功，插入後的中序遍歷結果：");
		in_traverse(pTree);
		printf("\n");
	}
	else
		printf("刪除失敗，該二叉排序樹中不存在整數%d\n",key);

	return 0;
}

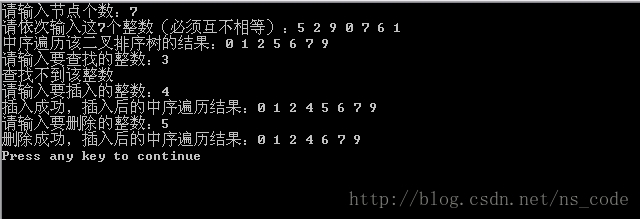
    測試結果如下：





相關文章