【資料結構與演算法】模式匹配——從BF演算法到KMP演算法（附完整原始碼）

蘭亭風雨發表於2014-02-20
資料結構演算法模式KMP原始碼

轉載請註明處處：http://blog.csdn.net/ns_code/article/details/19286279


模式匹配

    子串的定位操作通常稱為串的模式匹配。模式匹配的應用很常見，比如在文書處理軟體中經常用到的查詢功能。我們用如下函式來表示對字串位置的定位：

int index(const string &Tag,const string &Ptn,int pos)

    其中，Tag為主串，Ptn為子串（模式串），如果在主串Tag的第pos個位置後存在與子串Ptn相同的子串，返回它在主串Tag中第pos個字元後第一次出現的位置，否則返回-1。


BF演算法

    我們先來看BF演算法(Brute-Force，最基本的字串匹配演算法)，BF演算法的實現思想很簡單：我們可以定義兩個索引值i和j，分別指示主串Tag和子串Ptn當前正待比較的字元位置，從主串Tag的第pos個字元起和子串Ptn的第一個字元比較，若相等，則繼續逐個比較後續字元，否則從主串Tag的下一個字元起再重新和子串Ptn的字元進行比較，重複執行，直到子串Ptn中的每個字元依次和主串Tag中的一個連續字串相等，則匹配成功，函式返回該連續字串的第一個字元在主串Tag中的位置，否則匹配不成功，函式返回-1。

    用C++程式碼實現如下：

/*
返回子串Ptn在主串Tag的第pos個字元後(含第pos個位置)第一次出現的位置，若不存在，則返回-1
採用BF演算法，這裡的位置全部以從0開始計算為準，其中T非空，0<=pos<=Tlen
*/
int index(const string &Tag,const string &Ptn,int pos)
{
	int i = pos;  //主串當前正待比較的位置，初始為pos
	int j = 0;   //子串當前正待比較的位置，初始為0
	int Tlen = Tag.size();  //主串長度
	int Plen = Ptn.size();  //子串長度
	
	while(i<Tlen && j<Plen)
	{
		if(Tag[i] == Ptn[j])   //如果當前字元相同，則繼續向下比較
		{   
			i++;
			j++;
		}
		else   //如果當前字元不同，則i和j回退，重新進行匹配
		{   
			//用now_pos表示每次重新進行匹配時開始比較的位置，則
			//i=now_pos+後移量，j=0+後移量
			//則i-j+1=now_pos+1,即為Tag中下一輪開始比較的位置
			i = i-j+1;
			//Ptn退回到子串開始處
			j = 0;
		}
	}

	if(j >= Plen)
		return i - Plen;
	else
		return -1;
}

    呼叫上面的函式，採用如下程式碼測試：

int main()
{
	char ch;
	do{
		string Tag,Ptn;  
		int pos;
		cout<<"輸入主串：";
		cin>>Tag;
		cout<<"輸入子串：";
		cin>>Ptn;
		cout<<"輸入主串中開始進行匹配的位置（首字元位置為0）：";
		cin>>pos;
	
		int result = kmp_index(Tag,Ptn,pos);
		if(result != -1)
			cout<<"主串與子串在主串的第"<<result<<"個字元（首字元的位置為0）處首次匹配"<<endl;
		else
			cout<<"無匹配子串"<<endl;

		cout<<"是否繼續測試（輸入y或Y繼續，任意其他鍵結束）：";
		cin>>ch;
	}while(ch == 'y' || ch == 'Y');
	return 0;
}

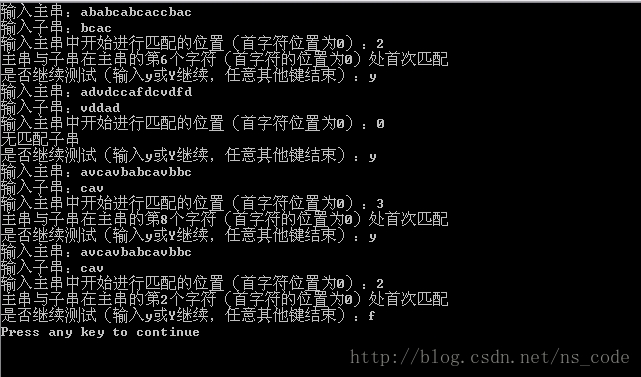
    測試結果如下：


    以上演算法完全可以實現要求的功能 ，而且在字元重複概率不大的情況下，時間複雜度也不是很大，一般為O（Plen+Tlen）。但是一旦出現如下情況，時間複雜度便會很高，如：子串為“111111110”，而主串為 “111111111111111111111111110” ，由於子串的前8個字元全部為‘1’，而主串的的前面一大堆字元也都為1，這樣每輪比較都在子串的最後一個字元處出現不等，因此每輪比較都是在子串的最後一個字元進行匹配前回溯，這種情況便是此演算法比較時出現的最壞情況。因此該演算法在最壞情況下的時間複雜度為O（Plen*Tlen），另外該演算法的空間複雜度為O（1）。


KMP演算法   

        KMP演算法的主要思想

    上述演算法的時間複雜度之所以大，是由於索引指標的回溯引起的，針對以上不足，便有了KMP演算法。KMP演算法可以在O（Plen+Tlen）的時間數量級上完成串的模式匹配操作。其改進之處在於：每一趟比較重出現字元不等時，不需要回溯索引指標i，而是利用已經得到的部分匹配的結果將子串向右滑動儘可能遠的距離，繼續進行比較。它的時間複雜度為O（Plen+Tlen），空間複雜度為O（Plen），這從後面的程式碼中可以看出。

    以下面兩個字串的匹配情況來分析

主串：ababcabcacbab

子串：abcac

    如果採用簡單的BF演算法，則每趟比較i都要回退，而採用KMP演算法，每趟比較時，i保持不變，只需將j向右滑動即可，也即是減少了中間一些趟次的比較。KMP演算法匹配以上兩個字元的過程如下（黃色部分表示匹配成功的位置，黃色部分的第一個字元表示該趟比較開始匹配的第一個字元，紅色部分表示匹配失敗的位置，綠色表示尚未進行比較的位置）：

    第一趟比較：在i=2和j=2處出現不匹配，如下圖中紅色部分所示

    第二趟比較：i不變，依然在主串的第2個字元處，子串向右滑動，相當於j回退，此趟比較從i=2和j=0處開始，在i=6和j=4處出現不匹配，如下圖中紅色部分所示


    第三趟比較：i依然在主串的第6個字元處，子串向右滑動，此趟比較從i=6和j=1處開始，最終匹配成功


    我們可以看到，只用3趟就可以完成匹配，而採用BF演算法則要6趟才能完成。為什麼可以這樣移動呢？我們從第一趟比較的結果得知，主串的第2個字元為b，而子串的第一個字元為a，因此，因此可以直接將BF演算法的第二趟比較省去，而直接進入第三趟比較，也就是KMP演算法的第二趟比較，再往後面，通過該趟比較，我們又知道主串的第4、5、6個字元必然是bca，它們無須再與子串的第一個字元比較，這樣便可以直接從i=6和j=1處進行比較。

    這裡的關鍵問題：每趟匹配過程中產生失配時，子串該向右滑動多遠，換句話說，當主串的第i個字元和子串的第j個字元失配時，下一趟比較開始時，主串的第i個字元應該與子串的哪個字元再去比較。這個問題我們在後面討論，我們先將KMP演算法的程式碼給出，我們假設失配時，主串的第i個字元與子串中的第next[j]個字元進行比較，並令j=0時，即在第一個字元處適時，next[j]=-1,則那麼我們可以寫出KMP演算法的程式碼如下：

/*
返回子串Ptn在主串Tag的第pos個字元後(含第pos個位置)第一次出現的位置，若不存在，則返回-1
採用KMP演算法，這裡的位置全部以從0開始計算為準，其中T非空，0<=pos<=Tlen
*/
int kmp_index(const string &Tag,const string &Ptn,int pos)
{
	int i = pos;  //主串當前正待比較的位置，初始為pos
	int j = 0;   //子串當前正待比較的位置，初始為0
	int Tlen = Tag.size();  //主串長度
	int Plen = Ptn.size();  //子串長度
	
	while(i<Tlen && j<Plen)
	{
		if(j==-1 || Tag[i] == Ptn[j])   
		{   //如果當前字元相同，或者在子串的第一個字元處失配，則繼續向下比較
			i++;
			j++;
		}
		else   //如果當前字元不同，則i保持不變，j變為下一個開始比較的位置
		{   
			//next陣列是KMP演算法的關鍵，i不回退，
			//而是繼續與子串中的nex[j]位置的字元進行比較
			j = next[j];
		}
	}

	if(j >= Plen)
		return i - Plen;
	else
		return -1;
}

   

   字首陣列next的求解  

    以上程式碼很簡單，也很容易理解，對照BF演算法，並沒有該幾行程式碼，關鍵在於如何求next陣列（也叫字首陣列），下面我們著重來看next陣列的求法。

    我們假設主串為“T0T1...Tn-1”,子串為“P0P1...Pm-1”在失配後，主串中的第i個字元應與子串中的第k（0<k<j，且是可以移動的最大值）個字元繼續比較，則子串中的前k-1個字元必須要滿足如下關係式：

P0 P1 ... Pk-1 = Ti-k Ti-k+1 ... Ti-1

    而我們由上一趟的比較，已經得到了如下匹配結果：

P0 P1 ... Pj-1 = Ti-j Ti-j+1 ... Ti-1

    我們取其中的部分匹配結果，如下：

Pj-k Pj-k+1 ... Pj-1 = Ti-k Ti-k+1 ... Ti-1

    比較第一個公式和第三個公式，我們便可以得出如下結果：

P0 P1 ... Pk-1 = Pj-k Pj-k+1 ... Pj-1

    這樣，所有的問題就轉移到子串Ptn上了，因此next陣列元素的值只與子串的形式有關，而與主串沒有任何關係。如果在子串中存在滿足上式的的兩個子字串，則在失配後，下一趟比較僅需從子串Ptn的第k個字元與主串Tag的第i個字元開始。於是可以令next[j]的表示式如以下三種情況所示：

    （1）當j>0時，next[j] = Max{k|k滿足 0<k<j 且 P0 P1 ... Pk-1 = Pj-k Pj-k+1 ... Pj-1}

    （2）當j=0時，next[j] = -1

    （3）當j>0且又不存在滿足 P0 P1 ... Pk-1 = Pj-k Pj-k+1 ... Pj-1 的k時，next[j] = 0

    
    先來看如何手算next陣列的值，再看如何用程式求解next陣列的值。

    首先看如何手算next陣列各元素值。
    我們來看如下字串：
abaabcac
  • 對於第0個字元a，根據情況2，next[0] = -1；
  • 對於第1個字元b，由於其前面只有1個字元a，故根據情況3，next[1] = 0；
  • 對於第2個字元a，其前面有2個字元ab，不存在與b或ab相等的字元，因此根據情況3，next[2] = 0；
  • 對於第3個字元a，其前面有3個字元aba，最長只有字元（第0個）和第2個字元a（緊跟第3個字元）相等，因此根據情況1，next[3] = 1；
  • 對於第4個字元b，其前面有4個字元abaa，最長只有字元（第0、2個）和第3個字元a（緊跟第4個字元）相等，因此根據情況1，next[4] = 1；
  • 對於第5個字元c，其前面有5個字元abaab，最長有子串ab（第0、第1個字元的組合）和第3、第4個字元的組合ab（緊跟第5個字元）相等，因此根據情況1，next[5] = 2；
  • 對於第6個字元a，其前面有6個字元abaabc，沒有子串與含有c（緊跟第6個字元）的字串相等，因此根據情況3，next[6] = 0；
  • 對於第7個字元c，其前面有7個字元abaabca，最長只有字元與第6個字元a（緊跟著第7個字元）相等，因此根據情況1，next[7] = 1；
    只要子串不是很長，可以一眼求出next陣列中各元素的值。

    下面看如何用程式來求next陣列的值。

    如果已有next[j] = k（假設k為已知），這說明在子串的前j個字元中，存在前面推論出來的關係式：

P0 P1 ... Pk-1 = Pj-k Pj-k+1 ... Pj-1

    下面我們繼續求next[j+1]，這就要分兩種情況開看：

    1、若Pk = Pj，則表明在子串中，有如下關係式：

P0 P1 ... Pk != Pj-k Pj-k+1 ... Pj

    那麼就有next[j+1] = k+1,即next[j+1] = next[j] + 1.

    2、若Pk != Pj，則表明在子串中，

P0 P1 ... Pk != Pj-k Pj-k+1 ... Pj

    此時，我們同樣可以將其看做是一個模式匹配的過程（子串與主串均為Ptn），由於Pk != Pj，首次出現不匹配，那麼應該取子串的第next[k]個字元與主串的第j個字元再做比較。

    我們假設next[k] = t，重複上面的比較，如果Pt = Pj，則next[j+1] = t + 1 = next[k] + 1，而如果Pt != Pj，則繼續講子串向右滑動，取其第next[t]個字元與子串的第j個字元再做比較，直到Pj和子串中的某個字元匹配成功，此時next[j+1]即為求得的值，或不存滿足上述等式的k，此時next[j+1] = 0.

    同樣以如下字串為例進行計算：

abaabcac

  • 對於第0個字元a，根據情況2，next[0] = -1；
  • 對於第1個字元b，由於其前面的字串a中不存在滿足上面等式的k，因此根據情況3，next[1] = 0；
  • 對於第2個字元a，由於其前面的字串ab中不存在滿足上面等式的k，因此根據情況3，next[2] = 0；
  • 對於第3個字元a，其前面的字串為aba，由於P0=P2，因此next[3] = 1；
  • 對於第4個字元b，其前面的字串為abaa，由於next[3]=1，而P3!=P1，則需要比較P3和P0（next[1]=0），而P3=P0，因此next[3] = next[1]+1 = 1；
  • 對於第5個字元c，其前面的字串為abaab，由於next[4]=1，而P4=P1，因此next[5] = next[4]+1 = 2；
  • 對於第6個字元a，其前面的字串為abaabc，由於next[5]=2，而P5!=P2，則需要比較P5和P0（next[2]=0），由於P5!=P0，因此不存在任何k值滿足上面的等式，next[6]=0；
  • 對於第7個字元c，其前面的字串為abaabc，由於next[6]=0，且P6=P0，因此next[7] = next[6]+1 = 1；

    依照KMP演算法，我們可以得到求next陣列的演算法，程式碼如下：

/*
求next陣列中各元素的值，儲存在長為len的next陣列中
*/
void get_next(const string &Ptn,int *next,int len)
{
	int j = 0;
	int k = -1;
	next[0] = -1;

	while(j<len-1)
	{
		if(k == -1 || Ptn[j] == Ptn[k])
		{   //如果滿足上面分析的Pk = Pj的情況，則繼續比較下一個字元，
			//並得next[j+1]=next[j]+1
			j++;
			k++;
			next[j] = k;
		}
		else
		{   //如果符合上面分析的第2種情況，則依據next[k]繼續尋找下一個比較的位置
			k = next[k];
		}
	}
}

    我們在程式中加入輸出next陣列的程式碼，測試KMP演算法，得到的結果如下：


   字首陣列next的改進  

    上面定義的next陣列在某些情況下是可以繼續改進的。考慮如下兩個字串：

主串：aaabaaaab

子串：aaaab

    通過手算，我們可以看出子串的next陣列的各元素為：-1、0、1、2、3。當主串和子串在第3個字元處出現不匹配時，即Tag[3]!=Ptn[3]，則由next[3]=2，因此需要比較Tag[3]和Ptn[2]，再根據next[2]=1，接下來需要繼續比較Tag[3]和Ptn[1]，再比較Tag[3]和Ptn[0]。而實際上，由於子串中的Ptn[0]、Ptn[1]和Ptn[2]這3個字元和主串中的Tag[3]相等，因此不需要再一一進行比較，可以直接進行Tag[4]和Ptn[0]的比較。

    針對普遍情況而言，若next[j] = k,且子串中Ptn[j] = Ptn[k]，則當Tag[i]!=Ptn[j]時，不需要再將Tag[i]和Ptn[k]進行比較，而可以直接和Ptn[next[k]]進行比較，也即是，next[j]=next[k]，而不是next[j]+1。因此上面求next陣列的程式碼可以修改如下：

/*
求next陣列的改進陣列中各元素的值，儲存在長為len的nextval陣列中
*/
void get_nextval(const string &Ptn,int *nextval,int len)
{
	int j = 0;
	int k = -1;
	nextval[0] = -1;

	while(j<len-1)
	{
		if(k == -1 || Ptn[j] == Ptn[k])
		{   //如果滿足上面分析的Pk = Pj的情況，則繼續比較下一個字元，
			//並得next[j+1]=next[j]+1
			j++;
			k++;
			if(Ptn[j] != Ptn[k])
				nextval[j] = k;
			else  //Ptn[j]與Ptn[k]相等時，直接跳到netval[k]
				nextval[j] = nextval[k];
		}
		else
		{   //如果符合上面分析的第2種情況，則依據next[k]繼續尋找下一個比較的位置
			k = nextval[k];
		}
	}
}
    這樣，子串aaaab的nextval陣列的各元素為：-1、-1、-1、-1、3。


完整程式碼下載

    完整的C++實現程式碼下載地址：http://download.csdn.net/detail/mmc_maodun/6937813

    

相關文章