【資料結構與演算法】Huffman樹&&Huffman編碼(附完整原始碼)
轉載請註明出處:http://blog.csdn.net/ns_code/article/details/19174553
Huffman Tree簡介
赫夫曼樹(Huffman Tree),又稱最優二叉樹,是一類帶權路徑長度最短的樹。假設有n個權值{w1,w2,...,wn},如果構造一棵有n個葉子節點的二叉樹,而這n個葉子節點的權值是{w1,w2,...,wn},則所構造出的帶權路徑長度最小的二叉樹就被稱為赫夫曼樹。
這裡補充下樹的帶權路徑長度的概念。樹的帶權路徑長度指樹中所有葉子節點到根節點的路徑長度與該葉子節點權值的乘積之和,如果在一棵二叉樹中共有n個葉子節點,用Wi表示第i個葉子節點的權值,Li表示第i個也葉子節點到根節點的路徑長度,則該二叉樹的帶權路徑長度 WPL=W1*L1 + W2*L2 + ... Wn*Ln。
根據節點的個數以及權值的不同,赫夫曼樹的形狀也各不相同,赫夫曼樹具有如下特性:
- 對於同一組權值,所能得到的赫夫曼樹不一定是唯一的。
- 赫夫曼樹的左右子樹可以互換,因為這並不影響樹的帶權路徑長度。
- 帶權值的節點都是葉子節點,不帶權值的節點都是某棵子二叉樹的根節點。
- 權值越大的節點越靠近赫夫曼樹的根節點,權值越小的節點越遠離赫夫曼樹的根節點。
- 赫夫曼樹中只有葉子節點和度為2的節點,沒有度為1的節點。
- 一棵有n個葉子節點的赫夫曼樹共有2n-1個節點。
Huffman Tree的構建
赫夫曼樹的構建步驟如下:
1、將給定的n個權值看做n棵只有根節點(無左右孩子)的二叉樹,組成一個集合HT,每棵樹的權值為該節點的權值。
2、從集合HT中選出2棵權值最小的二叉樹,組成一棵新的二叉樹,其權值為這2棵二叉樹的權值之和。
3、將步驟2中選出的2棵二叉樹從集合HT中刪去,同時將步驟2中新得到的二叉樹加入到集合HT中。
4、重複步驟2和步驟3,直到集合HT中只含一棵樹,這棵樹便是赫夫曼樹。
假如給定如下5個權值:

則按照以上步驟,可以構造出如下面左圖所示的赫夫曼樹,當然也可能構造出如下面右圖所示的赫夫曼樹,這並不是唯一的。
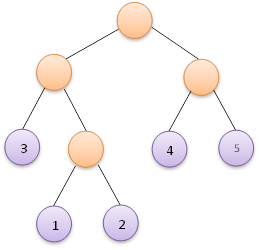
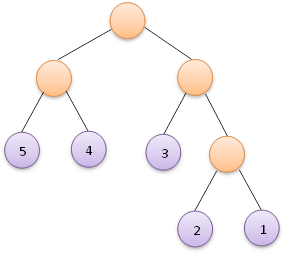
Huffman編碼
赫夫曼樹的應用十分廣泛,比如眾所周知的在通訊電文中的應用。在等傳送電文時,我們希望電文的總長儘可能短,因此可以對每個字元設計長度不等的編碼,讓電文中出現較多的字元采用盡可能短的編碼。為了保證在譯碼時不出現歧義,我們可以採取如下圖所示的編碼方式:
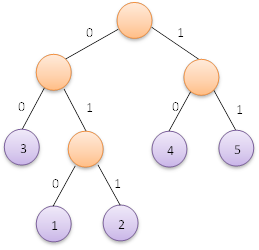
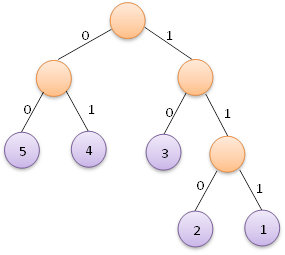
即左分支編碼為字元0,右分支編碼為字元1,將從根節點到葉子節點的路徑上分支字元組成的字串作為葉子節點字元的編碼,這便是赫夫曼編碼。我們根據上面左圖可以得到各葉子節點的赫夫曼編碼如下:
權值為5的也自己節點的赫夫曼編碼為:11
權值為4的也自己節點的赫夫曼編碼為:10
權值為3的也自己節點的赫夫曼編碼為:00
權值為2的也自己節點的赫夫曼編碼為:011
權值為1的也自己節點的赫夫曼編碼為:010
而對於上面右圖,則可以得到各葉子節點的赫夫曼編碼如下:
權值為5的也自己節點的赫夫曼編碼為:00
權值為4的也自己節點的赫夫曼編碼為:01
權值為3的也自己節點的赫夫曼編碼為:10
權值為2的也自己節點的赫夫曼編碼為:110
權值為1的也自己節點的赫夫曼編碼為:111
Huffman編碼的C實現
由於赫夫曼樹中沒有度為1的節點,則一棵具有n個葉子節點的的赫夫曼樹共有2n-1個節點(最後一條特性),因此可以將這些節點儲存在大小為2n-1的一維陣列中。我們可以用以下資料結構來表示赫夫曼樹和赫夫曼編碼:
/*
赫夫曼樹的儲存結構,它也是一種二叉樹結構,
這種儲存結構既適合表示樹,也適合表示森林。
*/
typedef struct Node
{
int weight; //權值
int parent; //父節點的序號,為-1的是根節點
int lchild,rchild; //左右孩子節點的序號,為-1的是葉子節點
}HTNode,*HuffmanTree; //用來儲存赫夫曼樹中的所有節點
typedef char **HuffmanCode; //用來儲存每個葉子節點的赫夫曼編碼/*
根據給定的n個權值構造一棵赫夫曼樹,wet中存放n個權值
*/
HuffmanTree create_HuffmanTree(int *wet,int n)
{
//一棵有n個葉子節點的赫夫曼樹共有2n-1個節點
int total = 2*n-1;
HuffmanTree HT = (HuffmanTree)malloc(total*sizeof(HTNode));
if(!HT)
{
printf("HuffmanTree malloc faild!");
exit(-1);
}
int i;
//以下初始化序號全部用-1表示,
//這樣在編碼函式中進行迴圈判斷parent或lchild或rchild的序號時,
//不會與HT陣列中的任何一個下標混淆
//HT[0],HT[1]...HT[n-1]中存放需要編碼的n個葉子節點
for(i=0;i<n;i++)
{
HT[i].parent = -1;
HT[i].lchild = -1;
HT[i].rchild = -1;
HT[i].weight = *wet;
wet++;
}
//HT[n],HT[n+1]...HT[2n-2]中存放的是中間構造出的每棵二叉樹的根節點
for(;i<total;i++)
{
HT[i].parent = -1;
HT[i].lchild = -1;
HT[i].rchild = -1;
HT[i].weight = 0;
}
int min1,min2; //用來儲存每一輪選出的兩個weight最小且parent為0的節點
//每一輪比較後選擇出min1和min2構成一課二叉樹,最後構成一棵赫夫曼樹
for(i=n;i<total;i++)
{
select_minium(HT,i,min1,min2);
HT[min1].parent = i;
HT[min2].parent = i;
//這裡左孩子和右孩子可以反過來,構成的也是一棵赫夫曼樹,只是所得的編碼不同
HT[i].lchild = min1;
HT[i].rchild = min2;
HT[i].weight =HT[min1].weight + HT[min2].weight;
}
return HT;
} 上述程式碼中呼叫到了select_minium()函式,它表示從集合中選出兩個最小的二叉樹,程式碼如下:
/*
從HT陣列的前k個元素中選出weight最小且parent為-1的兩個,分別將其序號儲存在min1和min2中
*/
void select_minium(HuffmanTree HT,int k,int &min1,int &min2)
{
min1 = min(HT,k);
min2 = min(HT,k);
}
/*
從HT陣列的前k個元素中選出weight最小且parent為-1的元素,並將該元素的序號返回
*/
int min(HuffmanTree HT,int k)
{
int i = 0;
int min; //用來存放weight最小且parent為-1的元素的序號
int min_weight; //用來存放weight最小且parent為-1的元素的weight值
//先將第一個parent為-1的元素的weight值賦給min_weight,留作以後比較用。
//注意,這裡不能按照一般的做法,先直接將HT[0].weight賦給min_weight,
//因為如果HT[0].weight的值比較小,那麼在第一次構造二叉樹時就會被選走,
//而後續的每一輪選擇最小權值構造二叉樹的比較還是先用HT[0].weight的值來進行判斷,
//這樣又會再次將其選走,從而產生邏輯上的錯誤。
while(HT[i].parent != -1)
i++;
min_weight = HT[i].weight;
min = i;
//選出weight最小且parent為-1的元素,並將其序號賦給min
for(;i<k;i++)
{
if(HT[i].weight<min_weight && HT[i].parent==-1)
{
min_weight = HT[i].weight;
min = i;
}
}
//選出weight最小的元素後,將其parent置1,使得下一次比較時將其排除在外。
HT[min].parent = 1;
return min;
} 構建了赫夫曼樹,便可以進行赫夫曼編碼了,要求赫夫曼編碼,就需要遍歷出從根節點到葉子節點的路徑,下面給出兩種遍歷赫夫曼樹求編碼的方法。
1、採用從葉子節點到根節點逆向遍歷求每個字元的赫夫曼編碼,程式碼如下:
/*
從葉子節點到根節點逆向求赫夫曼樹HT中n個葉子節點的赫夫曼編碼,並儲存在HC中
*/
void HuffmanCoding(HuffmanTree HT,HuffmanCode &HC,int n)
{
//用來儲存指向每個赫夫曼編碼串的指標
HC = (HuffmanCode)malloc(n*sizeof(char *));
if(!HC)
{
printf("HuffmanCode malloc faild!");
exit(-1);
}
//臨時空間,用來儲存每次求得的赫夫曼編碼串
//對於有n個葉子節點的赫夫曼樹,各葉子節點的編碼長度最長不超過n-1
//外加一個'\0'結束符,因此分配的陣列長度最長為n即可
char *code = (char *)malloc(n*sizeof(char));
if(!code)
{
printf("code malloc faild!");
exit(-1);
}
code[n-1] = '\0'; //編碼結束符,亦是字元陣列的結束標誌
//求每個字元的赫夫曼編碼
int i;
for(i=0;i<n;i++)
{
int current = i; //定義當前訪問的節點
int father = HT[i].parent; //當前節點的父節點
int start = n-1; //每次編碼的位置,初始為編碼結束符的位置
//從葉子節點遍歷赫夫曼樹直到根節點
while(father != -1)
{
if(HT[father].lchild == current) //如果是左孩子,則編碼為0
code[--start] = '0';
else //如果是右孩子,則編碼為1
code[--start] = '1';
current = father;
father = HT[father].parent;
}
//為第i個字元的編碼串分配儲存空間
HC[i] = (char *)malloc((n-start)*sizeof(char));
if(!HC[i])
{
printf("HC[i] malloc faild!");
exit(-1);
}
//將編碼串從code複製到HC
strcpy(HC[i],code+start);
}
free(code); //釋放儲存編碼串的臨時空間
} 我們以上面給出的5、4、3、2、1這五個權值為例,得到的編碼結果如下:
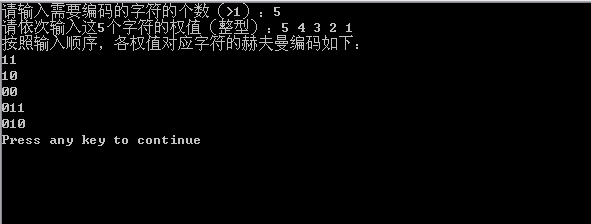
該方法是按照5、4、3、2、1的順序(也即是輸入的字元順序)來求每個字元的赫夫曼編碼的,同時也是按照這個順序列印到終端的。
2、採用從根節點到葉子節點無棧非遞迴遍歷赫夫曼樹,求每個字元的赫夫曼編碼,程式碼如下:
/*
從根節點到葉子節點無棧非遞迴遍歷赫夫曼樹HT,求其中n個葉子節點的赫夫曼編碼,並儲存在HC中
*/
void HuffmanCoding2(HuffmanTree HT,HuffmanCode &HC,int n)
{
//用來儲存指向每個赫夫曼編碼串的指標
HC = (HuffmanCode)malloc(n*sizeof(char *));
if(!HC)
{
printf("HuffmanCode malloc faild!");
exit(-1);
}
//臨時空間,用來儲存每次求得的赫夫曼編碼串
//對於有n個葉子節點的赫夫曼樹,各葉子節點的編碼長度最長不超過n-1
//外加一個'\0'結束符,因此分配的陣列長度最長為n即可
char *code = (char *)malloc(n*sizeof(char));
if(!code)
{
printf("code malloc faild!");
exit(-1);
}
int cur = 2*n-2; //當前遍歷到的節點的序號,初始時為根節點序號
int code_len = 0; //定義編碼的長度
//構建好赫夫曼樹後,把weight用來當做遍歷樹時每個節點的狀態標誌
//weight=0表明當前節點的左右孩子都還沒有被遍歷
//weight=1表示當前節點的左孩子已經被遍歷過,右孩子尚未被遍歷
//weight=2表示當前節點的左右孩子均被遍歷過
int i;
for(i=0;i<cur+1;i++)
{
HT[i].weight = 0;
}
//從根節點開始遍歷,最後回到根節點結束
//當cur為根節點的parent時,退出迴圈
while(cur != -1)
{
//左右孩子均未被遍歷,先向左遍歷
if(HT[cur].weight == 0)
{
HT[cur].weight = 1; //表明其左孩子已經被遍歷過了
if(HT[cur].lchild != -1)
{ //如果當前節點不是葉子節點,則記下編碼,並繼續向左遍歷
code[code_len++] = '0';
cur = HT[cur].lchild;
}
else
{ //如果當前節點是葉子節點,則終止編碼,並將其儲存起來
code[code_len] = '\0';
HC[cur] = (char *)malloc((code_len+1)*sizeof(char));
if(!HC[cur])
{
printf("HC[cur] malloc faild!");
exit(-1);
}
strcpy(HC[cur],code); //複製編碼串
}
}
//左孩子已被遍歷,開始向右遍歷右孩子
else if(HT[cur].weight == 1)
{
HT[cur].weight = 2; //表明其左右孩子均被遍歷過了
if(HT[cur].rchild != -1)
{ //如果當前節點不是葉子節點,則記下編碼,並繼續向右遍歷
code[code_len++] = '1';
cur = HT[cur].rchild;
}
}
//左右孩子均已被遍歷,退回到父節點,同時編碼長度減1
else
{
HT[cur].weight = 0;
cur = HT[cur].parent;
--code_len;
}
}
free(code);
} 該方法與方法1不同,它是根據赫夫曼樹的構造來求每個字元的編碼的,程式構造的赫夫曼樹如上圖中的左圖所示,那麼該方法便是按照3、1、2、4、5的順序來球每個字元的赫夫曼編碼的,但是我們在main函式中將其按照輸入的順序(5、4、3、2、1)列印到了終端。
完整程式碼下載
完整的程式碼下載地址
第一版:只含第一種編碼方法:
第二版:含有兩種編碼方法,並對部分程式碼做了些改進:
相關文章
- 【資料結構與演算法】字典樹(附完整原始碼)資料結構演算法原始碼
- Huffman對檔案編碼和解碼
- Huffman編碼m檔案分析
- Huffman演算法演算法
- 貪心演算法——Huffman 壓縮編碼的實現演算法
- 【資料結構與演算法】HashTable相關操作實現(附完整原始碼)資料結構演算法原始碼
- 05-樹9 Huffman Codes
- 【資料結構與演算法】二叉排序樹C實現(含完整原始碼)資料結構演算法排序原始碼
- 【資料結構與演算法】模式匹配——從BF演算法到KMP演算法(附完整原始碼)資料結構演算法模式KMP原始碼
- 【資料結構與演算法】自己動手實現圖的BFS和DFS(附完整原始碼)資料結構演算法原始碼
- 【資料結構與演算法】內部排序之三:堆排序(含完整原始碼)資料結構演算法排序原始碼
- 【資料結構與演算法】內部排序總結(附各種排序演算法原始碼)資料結構演算法排序原始碼
- 用優先佇列構造Huffman Tree及判斷是否為最優編碼的應用佇列
- 用 Huffman 樹實現檔案壓縮並解壓
- react原始碼ReactTreeTraversal.js之資料結構與演算法React原始碼JS資料結構演算法
- redis資料結構原始碼閱讀——字串編碼過程Redis資料結構原始碼字串編碼
- 資料結構與演算法:AVL樹資料結構演算法
- 【資料結構與演算法】內部排序之二:氣泡排序和選擇排序(改進優化,附完整原始碼)資料結構演算法排序優化原始碼
- Huffman Tree (use priority queue) in C++C++
- 樹形結構資料儲存方案(四):左右值編碼
- SICP:符號求導、集合表示和Huffman樹(Python實現)符號求導Python
- 資料結構與演算法(十四)深入理解紅黑樹和JDK TreeMap和TreeSet原始碼分析資料結構演算法JDK原始碼
- Redis 資料結構與物件編碼 (Object Encoding)Redis資料結構物件ObjectEncoding
- 【資料結構與演算法】二叉樹資料結構演算法二叉樹
- 05 Javascript資料結構與演算法 之 樹JavaScript資料結構演算法
- 資料結構與演算法:哈夫曼樹資料結構演算法
- 資料結構與演算法——AVL樹簡介資料結構演算法
- 資料結構與演算法——RB樹簡介資料結構演算法
- 【資料結構與演算法】內部排序之五:計數排序、基數排序和桶排序(含完整原始碼)資料結構演算法排序原始碼
- 【資料結構與演算法】內部排序之一:插入排序和希爾排序的N中實現(不斷優化,附完整原始碼)資料結構演算法排序優化原始碼
- 演算法與資料結構--簡析紅黑樹演算法資料結構
- 資料結構與演算法(十三)——紅黑樹1資料結構演算法
- 資料結構與演算法(十三)——紅黑樹2資料結構演算法
- 【資料結構與演算法】手撕紅黑樹資料結構演算法
- 資料結構與演算法:二叉排序樹資料結構演算法排序
- 資料結構與演算法——單詞查詢樹資料結構演算法
- javascript資料結構與演算法-- 二叉樹JavaScript資料結構演算法二叉樹
- 資料結構與演算法——赫夫曼樹(哈夫曼樹)資料結構演算法