從統計學角度來看深度學習(2):自動編碼器和自由能
作者:Shakir Mohamed 翻譯:鍾琰 審校:何通 編輯:王小寧
本文得到了原英文作者Shakir Mohamed的授權同意,由鍾琰翻譯、何通審校。感謝他們的支援和幫助。
基於前饋深度神經網路的判別模型已經在許多工業應用中獲得了成功,引發了探尋如何利用無監督學習方法帶來相似結果的熱潮。降噪自動編碼器是深度學習中一種主要的無監督學習方法。本文將探索降噪自編碼器和統計學中密度估計之間的聯絡,我們將從統計學的視角去考察降噪自動編碼器學習方法,並將之視為一種潛在因子模型的推斷問題。我們的機器學習應用能從這樣的聯絡中獲得啟發並受益。
廣義的降噪自動編碼器(GDAEs)
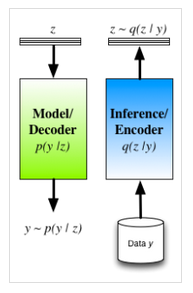
降噪自動編碼器是無監督深度學習中的一個重大進步,它極大的提升了資料表示的可擴充套件性和穩健性。對每個資料點y,降噪自動編碼器先利用一個已知的噪化過程C(y′|y)建立一個y的含噪聲版本y′,其後我們以y′為輸入利用神經網路來重新恢復原始資料y。整個學習網路可以被分為兩個部分:編碼器和解碼器,其中編碼器z的輸出可被認為是原始資料的一種表示或特徵。該問題的目標函式如下[1]:
Perturbation:y′∼C(y′|y)
Encoder:z(y′)=fϕ(y′)Decoder:y≈gθ(z)
Objective:LDAE=logp(y|z)
其中logp(⋅)是一個依資料選擇的對數似然函式,同時目標函式是所有觀測點上對數似然函式的平均。廣義降噪自編碼器(GDAEs)考慮到這個目標函式受制於有限的訓練資料,從而在原有公式的基礎上引入了一個額外的懲罰項R(⋅)[2]:
LGDAE=logp(y|z)–λR(y,y′)
GDAEs方法的原理是觀測空間上的擾動能增強編碼器結果z的穩健性和不敏感性。使用GDAEs時,我們需要注意兩個關鍵的問題:1)如何選擇一個符合實際的噪化過程;2)如何選擇合適的調整函式R(⋅)。
分離模型與推斷
從統計上推導自編碼器的困難在於: 它們並不能區分資料模型(反映我們對資料性質和結構的預期的統計假設)和推斷估計方法(我們將觀測資料聯絡到模型假設的種種方法)。自編碼器學習框架提供的是一套計算流程,而非統計解釋。當我們要解釋一個資料的時候,我們必須先了解資料再把它用作為輸入。不區分資料模型和推斷方法阻礙了我們去正確地評價並比較幾種候選方法的好壞,讓我們無法理解文獻中那些能帶來啟發的相關方法,使我們難以利用學術界廣闊的知識。
為了減輕這些憂慮,我們不妨將通過把解碼器看做是統計模型(實踐中確實有很多自編碼器的解釋與應用)來重新理解自編碼器。一個概率解碼器能提供資料的生成性描述,而我們的任務是對這個模型進行學習(或者推斷)。對一個給定的模型,有很多可以用來進行推斷的候選方法,如最大似然方法(ML),最大後驗概率估計(MAP),噪聲對比估計,馬爾可夫鏈蒙特卡爾理論(MCMC),變分推斷,腔方法(cavity methods),整合的巢狀拉普拉斯近似(INLA)等。因此編碼器的角色便十分明確:編碼器是對由解碼器描述的模型進行推斷的機制,它僅僅是現有的各式各樣的推斷方法中的一種,並且具有自己的優缺點。
潛因子模型中的近似推理
另一個DAEs的難點在於它的穩健性建立在對考察原始資料的干擾上。這樣一個噪化過程一般並不容易設計。此外,通過對概率分佈的推導,我們可以發現通過對對數噪化資料的密度函式logp(y′) 應用變分原理,我們可以得到DAE的目標函式LDAE的一個下界[1],然而並不是我們所感興趣的統計量。
一個可行的方法是將變分原理應用到我們感興趣的統計量上來,即對數觀測資料的邊際概率分佈logp(y)[3][4]。通過將變分原則應用到生成模型(概率解碼器模型)中能夠得到新的目標函式,我們稱其為變分自由能:
LVFE=Eq(z)[logp(y|z)]–KL[q(z)∥p(z)]
仔細觀察公式,我們可以發現它和GDAE的目標函式相符合。不過這裡仍然存在著以下幾點顯著的不同:
1)不同於考慮觀測值上的擾動,該公式考慮在隱藏值上通過z的先驗分佈p(z)獲得的擾動。這時隱藏層變數是隨機隱變數,而自編碼器是一個可以用來直接抽樣的生成模型。
2)編碼器q(z|y)用來近似潛變數的真實後驗分佈p(z|y)。
3)我們現在可以從理論上解釋GDAE目標函式中引入的懲罰函式。與其人為設計懲罰項,我們更應該推匯出這個懲罰函式的形式應該是先驗概率與編碼器分佈之間的KL距離。
從這個視角再次考察自編碼器,可以看到它是一種近似貝葉斯推斷的高效實現。利用一個編碼器-解碼器的結構,我們可以使用單個計算模型來優化所有引數。由於對測試資料僅需要一次前向計算,該方法能夠讓我們快速有效地進行統計推斷。使用這種方法的代價是我們將面臨一個更難的最優化問題,因為優化編碼器的引數讓我們同時耦合所有潛變數的推斷。那些不把q分佈作為一個編碼器的方法可以處理觀測資料中的任意缺失值,而我們的編碼器必須在已知缺失值模式的情況下進行訓練,沒有辦法處理觀測資料中任意缺失模式。我們使用的一種探究這個聯絡的方法是在深度隱高斯模型(DLGM)中基於隨機變分推斷(並利用一個編碼器進行實現)[3]進行統計推斷,這種方法現在是一系列擴充套件內容的基礎[5][6]。
總結
自動編碼器能夠用來解決統計推斷的問題,併為統計推斷提供了一個強而有力的方法,這一方法將在尋找更好的非監督學習方法中起到重要作用。使用統計學視角看待自編碼器,並使用變分法對其重塑,使得我們能很好地區分統計模型和推斷方法。於是我們能更有效地實現推斷,得到一個易於抽樣的生成模型,這允許我們研究所關心的統計量,並得到一個有重要懲罰項的損失函式。這是一個將會越來越流行的視角,在我們繼續探索非監督學習時也值得回顧。