【機器學習】--線性迴歸中L1正則和L2正則

LHBlog發表於2018-01-23
機器學習

一、前述

L1正則，L2正則的出現原因是為了推廣模型的泛化能力。相當於一個懲罰係數。

二、原理

L1正則：Lasso Regression

 

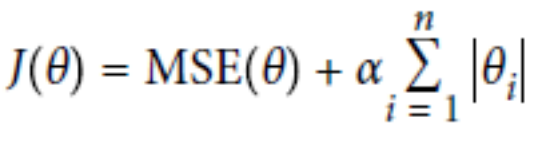
L2正則：Ridge Regression

總結：

經驗值 MSE前係數為1 ，L1 , L2正則前面係數一般為0.4~0.5 更看重的是準確性。

L2正則會整體的把w變小。

L1正則會傾向於使得w要麼取1，要麼取0 ，稀疏矩陣 ，可以達到降維的角度。

ElasticNet函式（把L1正則和L2正則聯合一起）：

總結：

1.預設情況下選用L2正則。

2.如若認為少數特徵有用，可以用L1正則。

3.如若認為少數特徵有用，但特徵數大於樣本數，則選擇ElasticNet函式。

 程式碼一：L1正則

# L1正則
import numpy as np
from sklearn.linear_model import Lasso
from sklearn.linear_model import SGDRegressor


X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

lasso_reg = Lasso(alpha=0.15)
lasso_reg.fit(X, y)
print(lasso_reg.predict(1.5))

sgd_reg = SGDRegressor(penalty='l1')
sgd_reg.fit(X, y.ravel())
print(sgd_reg.predict(1.5))

程式碼二：L2正則

# L2正則
import numpy as np
from sklearn.linear_model import Ridge
from sklearn.linear_model import SGDRegressor



X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

#兩種方式第一種嶺迴歸
ridge_reg = Ridge(alpha=1, solver='auto')
ridge_reg.fit(X, y)
print(ridge_reg.predict(1.5))#預測1.5的值
#第二種 使用隨機梯度下降中L2正則
sgd_reg = SGDRegressor(penalty='l2')
sgd_reg.fit(X, y.ravel())
print(sgd_reg.predict(1.5))

程式碼三：Elastic_Net函式

 

 

# elastic_net函式
import numpy as np
from sklearn.linear_model import ElasticNet
from sklearn.linear_model import SGDRegressor


X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
#兩種方式實現Elastic_net
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_net.fit(X, y)
print(elastic_net.predict(1.5))

sgd_reg = SGDRegressor(penalty='elasticnet')
sgd_reg.fit(X, y.ravel())
print(sgd_reg.predict(1.5))

 

相關文章