一.前述
線性迴歸是機器學習的基礎,所以比較重要。這裡邊線性是指一次,迴歸實際上就是擬合。Copy過來一段線性迴歸的描述如下:確定一個唯一的因變數(需要預測的值)和一個或多個數值型的自變數(預測變數)之間的關係。線性迴歸是一種有監督的機器學習,何謂有監督:實際上就是我們的資料集既要有X,又要有Y。
1、機器學習(資料探勘的一般過程):
定義挖掘目標
• 資料取樣
• 資料探索
• 資料預處理
• 挖掘建模
• 模型評價
2、舉例:
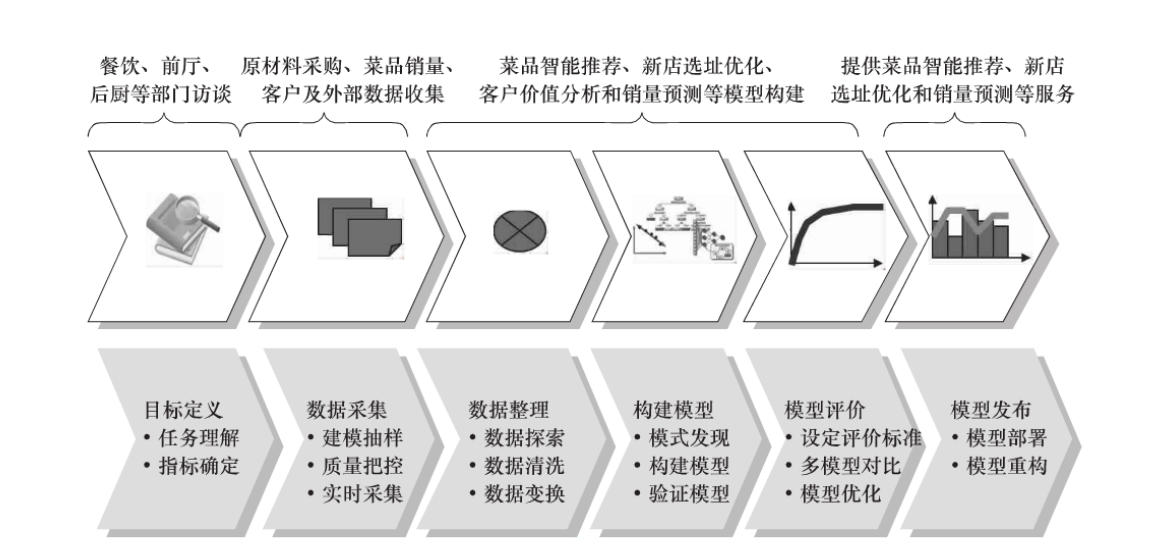
3、迴歸和分類的模型區別
有些Y標記是連續的,迴歸
有些Y標記是離散的,分類
二.原理
先明確幾個概念:
1.比如y=a+bx是我們根據樣本預測出來的曲線,那麼這裡面的a,b這些引數就是我們的模型(Model),我們的演算法(Algorithm)就是這裡面的公式。
2.最大似然估計(最大可能性概率):機器學習做的事情就是已知資料集X,Y求解擬合出來的曲線的引數w,而最大似然估計就是當w取什麼值的時候代入公式中,x,y的出現概率最大。
3.大自然的一切都是迴歸到一定區間之內的也就是趨於平均,所以我們可以大膽假設兩個條件:
3.1 預測出來的預測值和真實值之間的誤差足夠多的情況下的疊加的分佈符合均值u為0,方差為某定值的正態分佈。
3.2 所有樣本獨立分佈。
相 關係數
• 兩個變數之間的相關係數是一個數,它表示兩個變數服從一條直線的關係有多麼緊密。
• 相關係數就是指Pearson相關係數,它是數學家Pearson提出來的,相關係數的範圍是-1~+1之間,兩端的值表示一個完美
的線性關係。
• 相關係數接近於0則表示不存線上性關係。協方差函式cov(),標準方差函式sd(),可以求出來cor()。
誤差的概率密度函式:
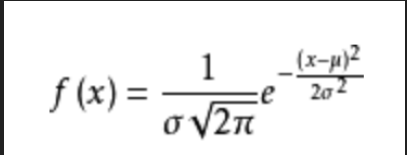
誤差函式:
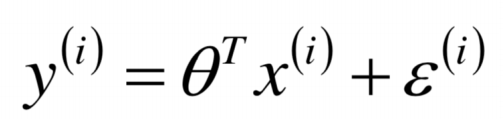
把誤差帶進來:
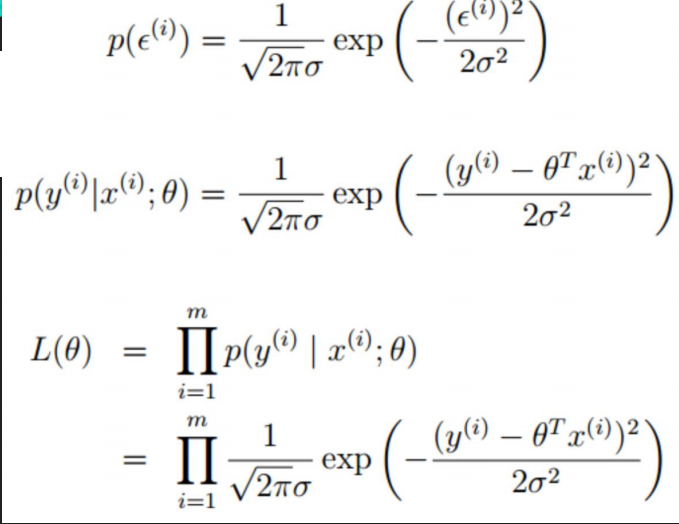
ps:以上最後求出最大似然估計,因為每個樣本點是相互獨立的,所以似然函式求最大,即為每個樣本點相乘。
上式中取Log函式即:

要使上面似然函式最大,也就是讓最後的誤差函式最小!!!!
所以有兩種辦法:
第一種解析解:
根據數學中函式對上式求導後求解可得。
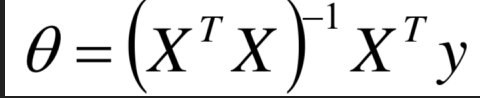
第二種最小梯度下降法:
梯度下降的核心是以最快的速度找到最優解 。我們的目的就是找到損失函式的一組w引數值,所以結合影像可知線性迴歸的影像是一個凸函式,也就是損失函式求導為0,也就是最低端與損失函式相切的那一組w引數。
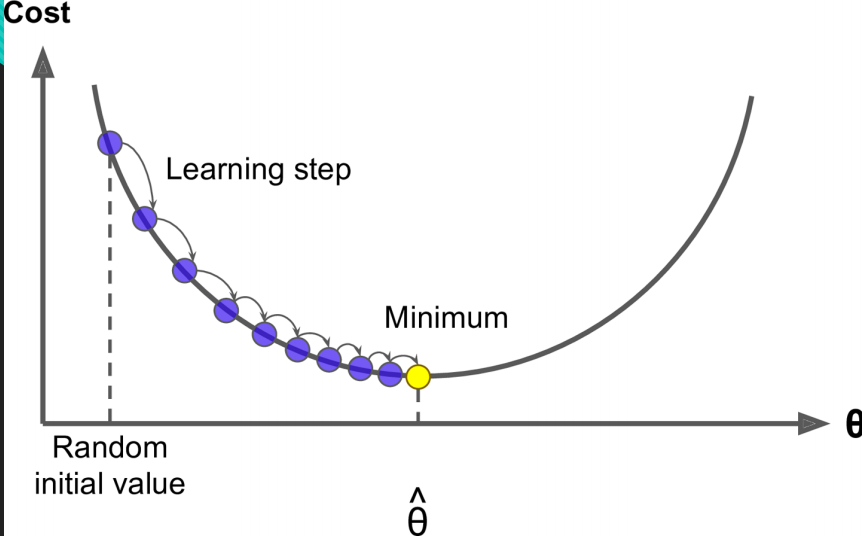
因為我們最終是要使損失函式減小,所以我們沿著損失函式的切線走會下降的最快:
我們有如下公式使每一次的損失函式都減小:
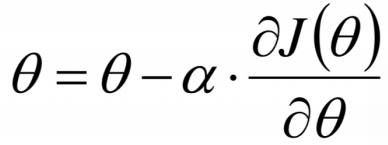
損失函式每一點的切線(也就是斜率,就是梯度)推導如下:
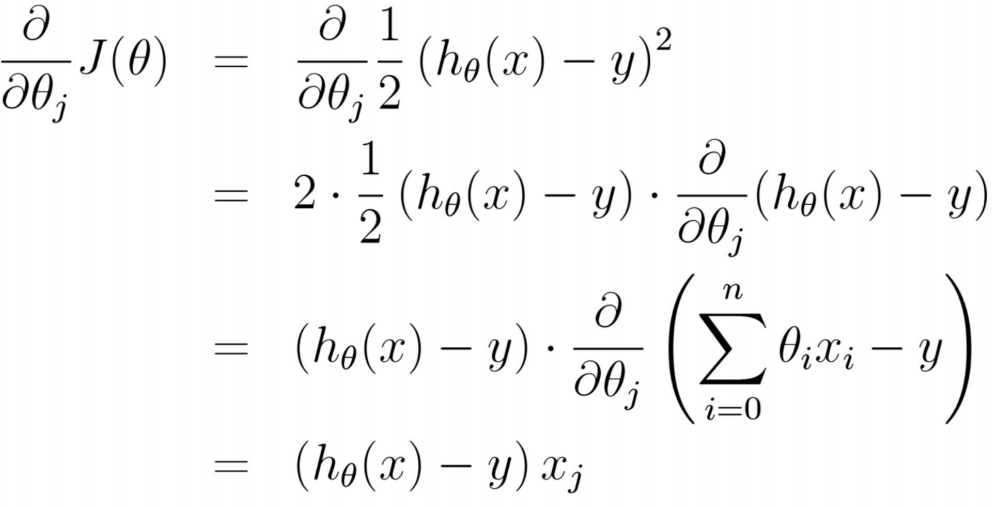
這裡有梯度下降裡面兩種方法來迭代:
第一:批量梯度下降公式:
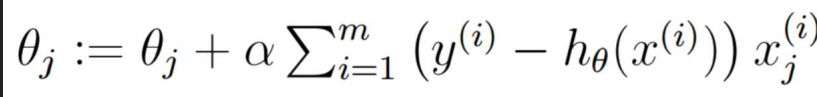
解剖公式:

所以總結如下:
每一個W調整都需要看每一個樣本的梯度加和求平均。相當於看清每一條路,然後選擇一個最好的。
1.每一次迭代每一個w調整的幅度是不一樣的,每一輪迭代之間的每一輪對應的w0(可以推理到w1,w2,w3,w4...)也都是不一樣的。
2.損失函式與w的影像中損失函式越小,每一組w與上一組w的差值也越來越小。如下圖:
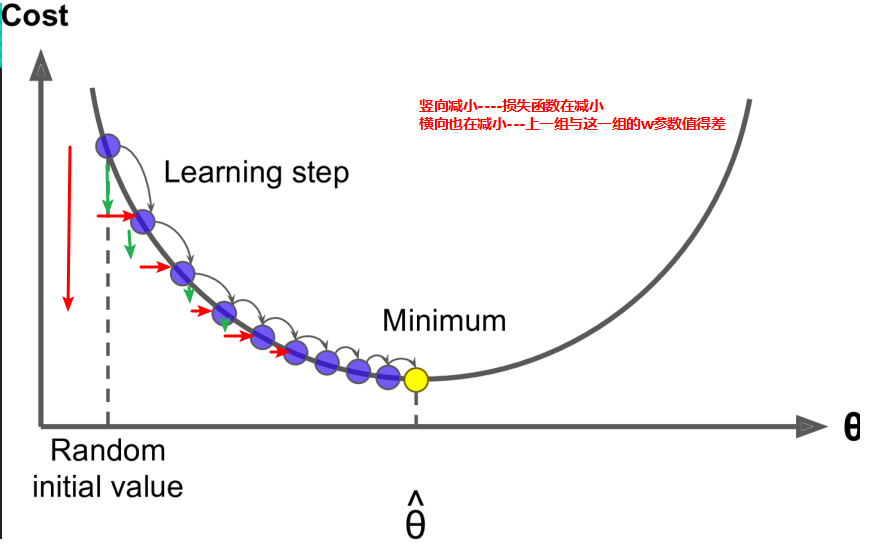
3.當Step(較小的時候),也就是步長較小的時候如圖,迭代次數比較多。
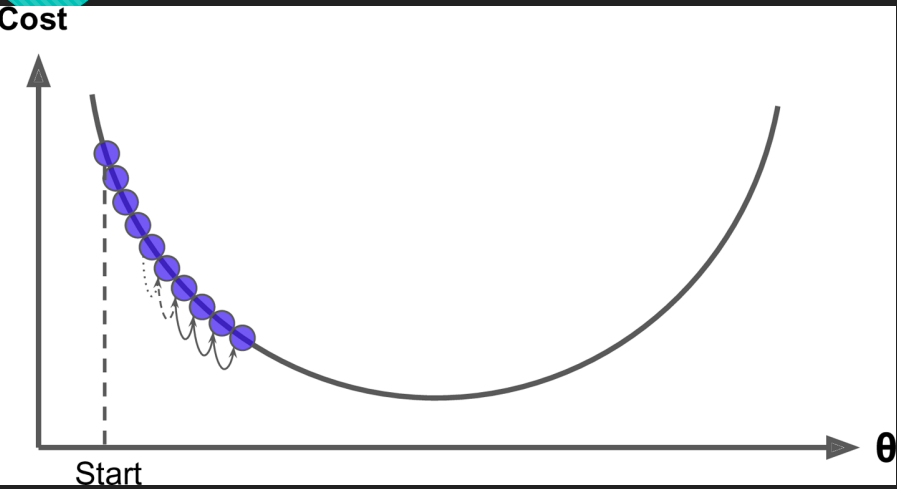
4.當Step(步長大的時候),會來回震盪,但有可能找到全域性最優解。
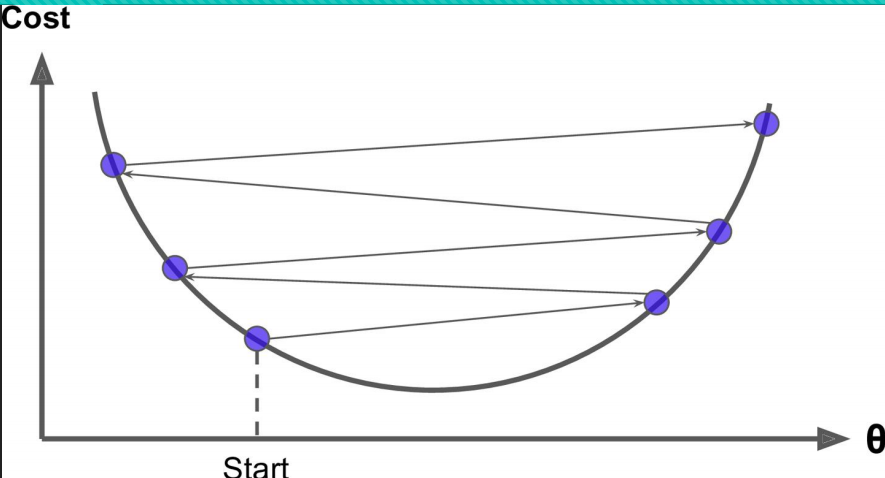
5.梯度下降一般找到的是區域性最優解,但模型一般堪用即可!!!!
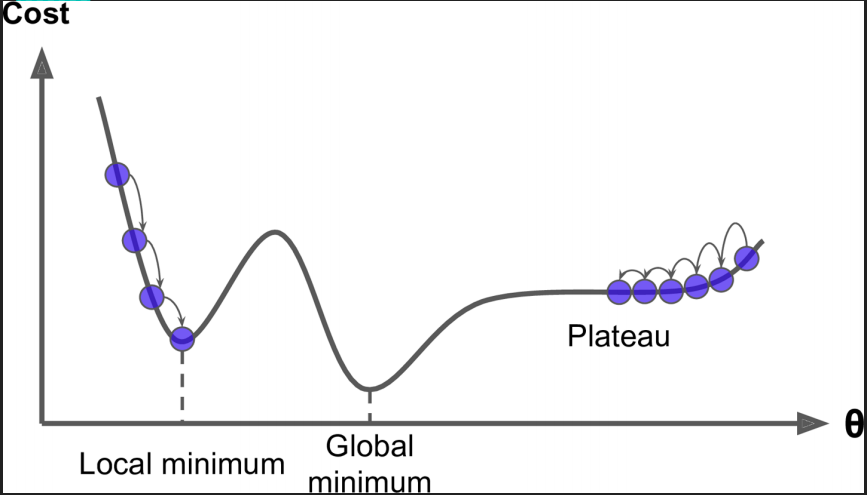
第二種:隨機梯度下降(優先選擇!!!!!)
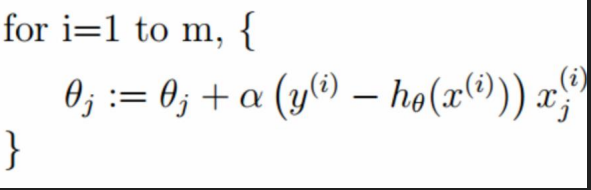
因為每一輪迭代不需要所有真實值與預測值的差再乘以所調整的w對應行的x的值,而是隨機選擇某一行計算.
舉例求w0:
(真實值-預測值)*該行對應的第一列的x的值即可求得w0,w1也是隨機找到一行對應相乘,這樣一組w求完,本輪迭代結束。開始下一輪。
總結:
1.優先隨機梯度下降,因為計算速度比較快。
2.隨機梯度下降可以跳出區域性最小值,因為有可能隨機到某一行真實值和誤差值相差較大,而對應的x也比較大,所以下降的幅度比較大,有可能找到最優解!!!
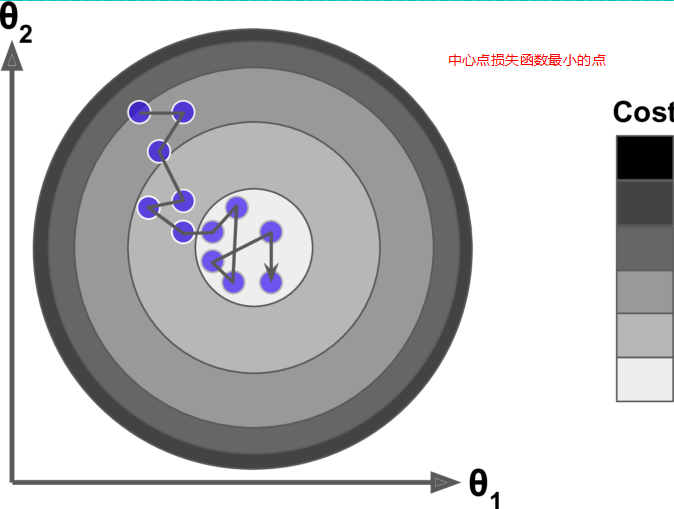
總結如下:

三、具體程式碼
線性迴歸初始程式碼:
#!/usr/bin/python # -*- coding: UTF-8 -*- # 檔名: insurance.py import pandas as pd import matplotlib.pyplot as plt from sklearn import linear_model data = pd.read_csv('./data/insurance.csv') print(type(data)) print(data.head()) print(data.tail()) # describe做簡單的統計摘要 print(data.describe()) # 取樣要均勻 data_count = data['age'].value_counts() print(data_count) data_count[:10].plot(kind='bar')#切片操作,取前10個,畫直方圖 plt.show() print(data.corr())#皮爾遜相關係數 +1正相關 -1負相關 不能僅根據相關係數就把維度去掉 reg = linear_model.LinearRegression() x = data[['age', 'sex', 'bmi', 'children', 'smoker', 'region']] y = data['charges'] #python3.6 報錯 sklearn ValueError: could not convert string to float: 'northwest',加入一下幾行解決 x = x.apply(pd.to_numeric, errors='coerce') y = y.apply(pd.to_numeric, errors='coerce') x.fillna(0, inplace=True)#如果碰到空值就轉換成0 y.fillna(0, inplace=True)#如果碰到空值就轉換成0 reg.fit(x, y) print(reg.coef_)# w1,w2,w3... print(reg.intercept_)#w0
解析解求解:
#!/usr/bin/python # -*- coding: UTF-8 -*- # 檔名: linear_regression_0.py import numpy as np import matplotlib.pyplot as plt X = 2 * np.random.rand(100, 1) y = 4 + 3 * X + np.random.randn(100, 1) X_b = np.c_[np.ones((100, 1)), X] print(X_b) # 常規等式求解theta theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y) print(theta_best) X_new = np.array([[0], [2]]) X_new_b = np.c_[(np.ones((2, 1))), X_new] print(X_new_b) y_predict = X_new_b.dot(theta_best) print(y_predict) plt.plot(X_new, y_predict, 'r-') plt.plot(X, y, 'b.') plt.axis([0, 2, 0, 15]) plt.show()
根據公式自定義批量梯度下降。
import numpy as np X = 2 * np.random.rand(100, 1) # 隨機取100個數,然後放到一列中去,是一個向量 y = 4 + 3 * X + np.random.randn(100, 1) # randn 正態分佈,(1列100行) 3,預測值 所以這裡是真實值 X_b = np.c_[np.ones((100, 1)), X] # 相當於100行兩列,第一列全是1 ,第二列是一個隨機的數 # print(X_b) learning_rate = 0.22 #學習率,步長 學習率,步長 當學習率小的時候,可能每到最優點時就停止迭代了。 n_iterations = 1000 #迭代100次 m = 100 # 100行樣本 theta = np.random.randn(2, 1)# 初始w值 count = 0 for iteration in range(n_iterations):# 0-999迭代 count += 1 gradients = 1/m * X_b.T.dot(X_b.dot(theta)-y)# 梯度 X_b.dot(theta)-y 是一個向量 X_b.T.dot乘以後面相當於矩陣的一個轉置乘以一個向量相當於每一行會分別相乘加和。和 theta = theta - learning_rate * gradients#每一次迭代,是一組數,相當於一組w引數都解出來了 print(count) print(theta)
結果:

自定義隨機梯度下降
import numpy as np X = 2 * np.random.rand(100, 1) y = 4 + 3 * X + np.random.randn(100, 1) X_b = np.c_[np.ones((100, 1)), X] # print(X_b) n_epochs = 50 #這些超引數都可以自己調整 t0, t1 = 5, 50 # 超引數 m = 100 def learning_schedule(t): return t0 / (t + t1) theta = np.random.randn(2, 1) #初始一組w值 for epoch in range(n_epochs): # 50次 0-50 for i in range(m): #100次 0-99 random_index = np.random.randint(m) #隨機取一行,拿到這一行的標號 xi = X_b[random_index:random_index+1] #取這行的所有X值,切片左閉右開 yi = y[random_index:random_index+1]#取這行的Y值 gradients = 2*xi.T.dot(xi.dot(theta)-yi)#(誤差-真實值)*這一行的x值 learning_rate = learning_schedule(epoch*m + i) #epoch*m+i越來越大 帶到上面函式中,學習率越來越小 讓步長越來越小 不會隨機太大 theta = theta - learning_rate * gradients print(theta) #PS 總結:迭代次數多了,但每一次迭代不用加和,每一次的迭代計算小了
結果:
 結
結
sk_learn中隨機梯度下降公式
import numpy as np from sklearn.linear_model import SGDRegressor X = 2 * np.random.rand(100, 1) y = 4 + 3 * X + np.random.randn(100, 1) sgd_reg = SGDRegressor(n_iter=50, penalty=None, eta0=0.1) # n_iter 步長 penalty 懲罰係數 eta0 最舒適的學習率,學習率不斷下降 # print(X) # print(y.ravel())# 相當於flat 壓扁壓平 多行一列的資料壓扁成一行。。。一個行向量。 sgd_reg.fit(X, y.ravel()) #因為這個函式需要的y是一個行向量,所以壓扁。 print(sgd_reg.intercept_, sgd_reg.coef_) # intercept_ w0 coef_ w1,w2,w3多個引數。
程式碼中sk_learn中學習率原始碼:可以發現學習率也是越來越小的。

PS:總結批量梯度下降裡面我們要調整迭代次數和學習率,隨機梯度下降裡面我們要調整迭代次數和學習率,讓學習率越來越小。