【機器學習】---密度聚類從初識到應用

LHBlog發表於2018-01-19
機器學習聚類

一.前述

密度聚類是一種能降噪的演算法。很多時候用在聚類形狀不規則的情況下。

二.相關概念

先看些抽象的概念（官方定義）：

1.：物件O的是與O為中心，為半徑的空間，引數，是使用者指定每個物件的領域半徑值。

2.MinPts（領域密度閥值）：物件的的物件數量。

3.核心物件：如果物件O的物件數量至少包含MinPts個物件，則該物件是核心物件。

4.直接密度可達：如果物件p在核心物件q的內，則p是從q直接密度可達的。

5.密度可達：在DBSCAN中，p是從q(核心物件)密度可達的，如果存在物件鏈，使得,是從關於和MinPts直接密度可達的，即在的

內，則到密度可達。

6.密度相連：如果存在物件，使得物件都是從q關於和MinPts密度可達的，則稱是關於和MinPts密度相連的。

PS：是不是很抽象 ，所以官方定義永遠是官方定義確實理解不了。然後再看些非官方定義，其實就大概明白了。

先上圖：

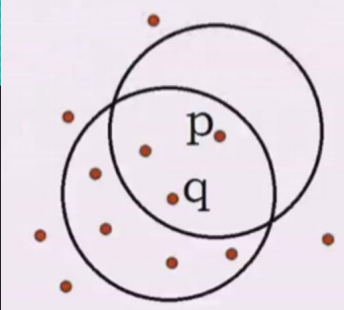
解釋下：這裡有幾個關鍵的概念。

領域其實就是某一個半徑內，假設半徑為5，我們先看P點以半徑為5畫的圓中包含3個點，而q點以半徑為5畫7個點  7>5,所以q就叫做核心物件。q不是核心物件。理解就是這麼簡單，再看看什麼叫密度可達，見下圖：

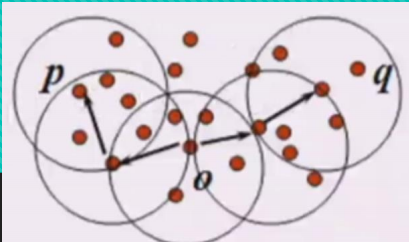
0點以半徑為5畫圓與p點以半徑為5畫圓有交集，即O點以半徑為5的領域內有以P為中心店半徑為5的領域內的點，則O密度可達P，O也密度可達q(在邊界交點也算)。

從o點能密度可達p，也能密度可達q,則p,q叫密度相連。

再比如：

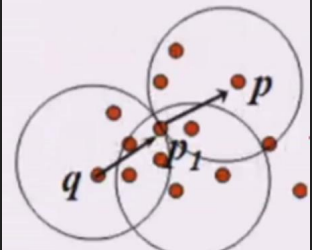
q密度可達p1，p1密度可達p，則q密度可達p（間接的也是密度可達）！！！！

這裡需要兩個引數注意下：r半徑，m閾值，即以r為半徑內所包含的點，只有大於m閾值的點才能叫核心物件。

 以上理解了這些概念，但跟聚類有什麼相連，實際上簇就是密度相連的最大的集合。即一個簇就是最大的密度相連的集合。

如果一個點不是核心物件，也就意味著不能密度可達，所以就是噪聲點。（通俗理解就是一個點都不能畫圓，怎麼會有密度可達呢？）

比如下圖：

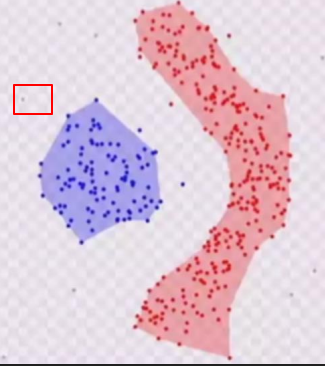
就是噪聲點。

PS：總結下規律：

給定的m不夠簇就會變多，比如下圖：m分別是5,3,2

 

解釋：當是5的時候，圈紅的邊緣點不是核心物件，所以不能畫圓，所以不會密度可達。當是2的時候，半徑內的值大於閾值所以是核心物件，那麼這堆資料有可能密度相連，形成一個簇。這也就是簇變多的原因。

程式碼：

 

# !/usr/bin/python
# -*- coding:utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt
import sklearn.datasets as ds
import matplotlib.colors
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler


def expand(a, b):
    d = (b - a) * 0.1
    return a-d, b+d


if __name__ == "__main__":
    N = 1000
    centers = [[1, 2], [-1, -1], [1, -1], [-1, 1]]
    data, y = ds.make_blobs(N, n_features=2, centers=centers, cluster_std=[0.5, 0.25, 0.7, 0.5], random_state=0)
    data = StandardScaler().fit_transform(data)
    # 資料的引數：(epsilon, min_sample)
    params = ((0.2, 5), (0.2, 10), (0.2, 15), (0.3, 5), (0.3, 10), (0.3, 15))

    matplotlib.rcParams['font.sans-serif'] = [u'SimHei']
    matplotlib.rcParams['axes.unicode_minus'] = False

    plt.figure(figsize=(12, 8), facecolor='w')
    plt.suptitle(u'DBSCAN聚類', fontsize=20)

    for i in range(6):
        eps, min_samples = params[i]
        model = DBSCAN(eps=eps, min_samples=min_samples)
        model.fit(data)
        y_hat = model.labels_

        core_indices = np.zeros_like(y_hat, dtype=bool)
        core_indices[model.core_sample_indices_] = True

        y_unique = np.unique(y_hat)
        n_clusters = y_unique.size - (1 if -1 in y_hat else 0)
        print(y_unique, '聚類簇的個數為：', n_clusters)

        plt.subplot(2, 3, i+1)
        clrs = plt.cm.Spectral(np.linspace(0, 0.8, y_unique.size))
        print(clrs)
        for k, clr in zip(y_unique, clrs):
            cur = (y_hat == k)
            if k == -1:
                plt.scatter(data[cur, 0], data[cur, 1], s=20, c='k')
                continue
            plt.scatter(data[cur, 0], data[cur, 1], s=30, c=clr, edgecolors='k')
            plt.scatter(data[cur & core_indices][:, 0], data[cur & core_indices][:, 1], s=60, c=clr, marker='o', edgecolors='k')
        x1_min, x2_min = np.min(data, axis=0)
        x1_max, x2_max = np.max(data, axis=0)
        x1_min, x1_max = expand(x1_min, x1_max)
        x2_min, x2_max = expand(x2_min, x2_max)
        plt.xlim((x1_min, x1_max))
        plt.ylim((x2_min, x2_max))
        plt.grid(True)
        plt.title(u'epsilon = %.1f  m = %d，聚類數目：%d' % (eps, min_samples, n_clusters), fontsize=16)
    plt.tight_layout()
    plt.subplots_adjust(top=0.9)
    plt.show()

 

 

 

r半徑太大就會聚類到一起：如下圖

 

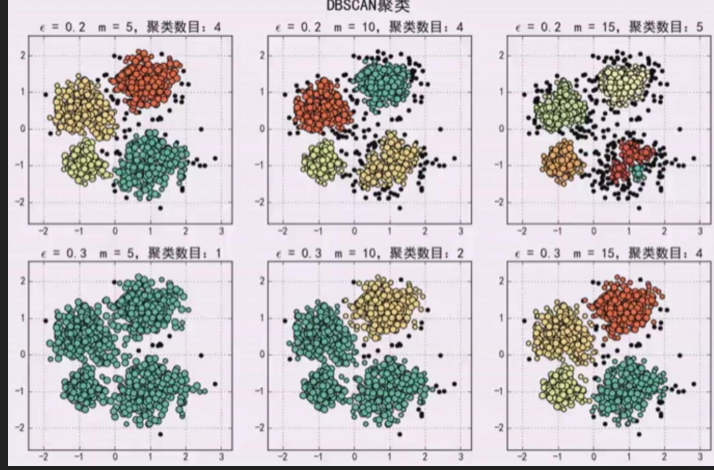
 所以Finally總結：要大一起大，要小一起小，引數這是最合適的。比如2,6圖是合適的，4個簇。

 未完待續，持續更新中。。。。。。。。。。。。

 

      

相關文章