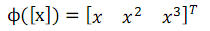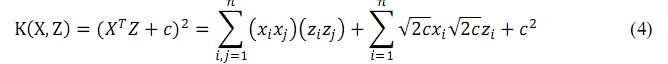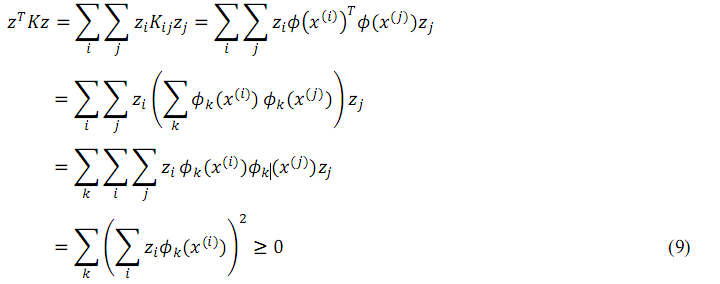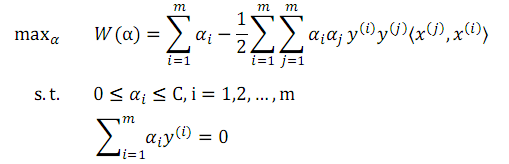課程概要：

1.核技法

2.軟間隔分類器

3.SVM求解的序列最小化演算法(SMO)

4.SVM應用

一.核技法

回憶一下上篇中得到的簡化的最優問題，，#1：

定義函式ϕ(x)為向量之間的對映，一般是從低維對映到高維，比如在前面筆記中提到的房價和麵積的關係問題中，可以定義ϕ為：

這樣，就可以將#1 問題中目標函式中的內積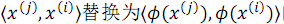的形式

這樣就達到了將低維空間上的資料對映到高維空間上，使資料線性可分的概率變大，即不能
保證在高維上一定是線性可分的，但一般情況下高維空間上比低維空間上更加線性可分。
但有些時候，經過ϕ對映後的向量的維度過高，導致對映後向量內積的計算複雜度過高。
為了解決這個問題，我們正式引入核函式：

其中，X,Z即為上面的為了簡化表示，去掉了上標。

核函式的作用在於定義了核函式後，可以不用明確的定義出對映函式，就能計算兩個向量在高維空間中的內積了，而且時間複雜度低。

下面舉幾個核函式的例子：

其對應的對映函式為

一個相似的核函式如下： 

其對應的對映函式為

一個更一般化的核函式如下：

該核函式對應的對映函式的結果是一個.大小的向量，向量中每個元素都是最高為d階的變數的組合。
對於公式2、 4、 6中的核函式而言，雖然它們對應的對映函式的維度可能是 n^2或者 n^d，意味著如果直接計算對映結果的內積的話複雜度分別為O(n^2)或O(n^d)，但是如果直接計算核函式的值，其複雜度均為O(n)，這也體現了核函式降低計算量的好處。

直觀上來看，如果ϕ(x)ϕ(z)在其對應的維度空間中位置接近，那麼內積值 K 會很大，反之則內積會小。這意味著核函式 K 是一個向量 x 和向量 z 何等接近的度量函式，從而可
以引出SVM中使用較廣泛的高斯核：

值得一提的是，高斯核對應的對映函式ϕ是對映到無限維的。
那麼，什麼樣的核函式才是正確的核函式，是不是所有的以 x，z 為變數的函式都能做核函式呢？即如何判斷一個函式是不是能拆分成對映函式乘積的形式？前後兩個問題等價
的原因是核函式是由對映函式乘積得到的，因而如果核函式合法，那麼必然能寫成兩個對映函式乘積的形式。

   為了解決這個問題，首先定義核矩陣。對於一個資料集,定義一個m*m的矩陣K（K既代表核函式也代表核矩陣），K中的每個元素定義如下：

對於核矩陣，有幾個性質，首先很顯然，Kij=Kji，核矩陣是一個對稱（symmetric）矩陣。
其次，對於任意的m維向量 z，可以得到：

由此，因為z是任意向量，所以 K是半正定（positive semi-definite）矩陣。事實上，這不僅是一個必要條件還是一個充分條件。因為存在一個 Mercer定理：
給定一個K：ℝ^n × ℝ^n ⟶ℝ，那麼K是合法的核（又稱 Mercer核）的充分必要條件是：
對於任意一個有限資料集，對應的核矩陣是對稱半正定矩陣。
對於核來說，不僅僅只存在於 SVM 內，對於任意的演算法，只要計算時出現了內積的，都可以用核函式替代，從而提高在高維資料上的效能，比如感知器演算法，代入後可發展為核感知器演算法。這也是核函式被稱為核技法的原因吧。

二、軟間隔分類器

之前講述最優間隔分類器時，一直強調資料是線性可分的。但是，當資料是線性不可分時，或者對映到高維空間後仍然不是線性可分，再或者即便是線性可分的但實際應用中不可避免出現噪聲時，該如何處理呢？本節提供了一個比較通用的解法。

首先，對原始問題進行變形，得到#2：

由#2可知，有些資料點可以被允許擁有比 1小的幾何間隔，但是這種情況要受到懲罰，C 為懲罰因子，是一個預設的引數。
其中，由目標函式的兩部分，w 部分和懲罰部分，按照它們的指數可以分為多種組合。
當 w 的指數為 n時，稱之為 Ln 正規化；當懲罰部分的指數為 n 時，稱之為 Ln 損失；比如
#2中的目標函式即為L2 正規化-L1損失 SVC（Support Vector Classification）1。
按照上篇筆記中的將原始問題轉化為對偶問題進行簡化的例子，寫出#2 對應的拉格朗日方程：

公式10中，α, r是拉格朗日乘子，均有不小於 0 的約束。

按照上篇筆記中的對偶問題的推導方式，先針對 w，b 最小化，然後再針對α最大化，得到新的對偶問題，即#3

與#1 對比得到，本問題只對αi做了進一步的約束。求解得到α後，w 仍然按照公式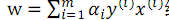給出，但是截距 b的得到方式要變化。

另一個發生變化的地方在於 KKT 中的互補條件，現在變為：

這些條件將在下一節用於判斷 SMO 演算法是否收斂。 至此，終於已經得到一個可以應用於實際的具體問題了（#1 是假設資料集線性可分，
不符合實際），下面一節將對介紹對#3問題求解的演算法。

三、SMO演算法

座標上升法

在介紹 SMO 演算法之前，先介紹一個簡化的但與 SMO 使用同一思想的演算法，座標上升法（Coordinate Ascent）。
先拋開SVM優化問題，看如下一個要解決的簡單的新問題：

對函式尋找最優值，之前已介紹了梯度下降法和牛頓法。現在介紹一種新方法：

最內層迴圈中，當更新i時，保持其它的引數不變。 直觀上看，這種方法比梯度下降和牛頓法迭代次數要多（一般情況下事實如此），
但當能很快的求解argmax時，該演算法仍是一個高效的演算法，下面是一種執行樣例圖：  由圖可見，當保持其它引數不變而只改
變某個引數時，會使得引數的收斂方向都是平行於座標軸的。 還有一點，這張圖只有兩個引數，所以才能在二維圖中展示出來。

SMO演算法

SMO（Sequential Minimal Optimization）與座標上升法不同的地方在於，由於#3 問題中有一個約束為 ，

使得當固定其他引數只改變一個引數的時候，發現剩餘的那個引數是固定的，因而SMO 演算法每次選擇兩個引數進行優化。實際上，兩個引數中可以將
一個當做變數，另外一個當做該變數的函式，函式關係為：

 SMO演算法描述為：

迴圈中，在選擇引數對時，使用一些啟發式規則選擇使全域性函式增長最大的引數。

前面提到，這種演算法雖然迭代次數多，但當最優化時速度快，仍不失為一種高效的演算法，那麼對於SVM最優化問題，優化起來效率如何呢？對於#3中的目標函式來說，當只保留兩個引數變化時，代入公式14的關係，那麼目標函式將變為一個二次函式，再加上0 ≤ αi ≤ C的條件，求最優值還是極為簡單的。

當然，在計算最優值時，需要根據約束關係對自變數的取值範圍進一步的計算，比如右圖所示，假設以α2為自變數，那麼它的範圍就是[L,H]。

四、SVM應用

SVM 作為一種分類器，自然在分類問題上大展手腳了。比如文字分類、影象分類等。
下面列舉幾個SVM的實際應用。
比如手寫數字識別問題，給定一張 16*16 的圖片，上面寫著 0-9的 10個數字，使用 SVM進行判定。這本來是NN（Neural Network）比較擅長的問題，但初次將SVM用於其上時效果之好令人驚訝，因為SVM沒有圖片識別的先驗知識，只是依據畫素就能達到很好的效果。
補充一點，SVM上使用高斯核和多項式核都能在該問題上達到和NN 相當的效果。 再比如通過氨基酸序列對蛋白質的種類進行判別，假設有 20 中氨基酸，它們按照不同
的序列可以組成不同的蛋白質，但這些氨基酸序列的長度差異很大，那麼該如何設定特徵呢？
有一種方式是使用連續四個氨基酸序列出現次數作為向量，比如氨基酸序列AABAABACDEF，那麼可以得到 AABA:2, ABAA:1,…CDEF:1。據此，可以得到特徵向量的
長度為204，如此大的特徵向量，難以載入記憶體，有一種高效的動態規劃演算法可以解決此問題。
與氨基酸序列識別蛋白質類似的是，字串的識別，對於長度為k 的字串，如果以字母為特徵，那麼特徵向量大小為 26k，也需要利用dp 演算法進行解決。