最近接觸了pLSA模型,由於該模型中引入了主題作為隱變數,所以需要使用期望最大化(Expectation Maximization)演算法求解。
本文簡述了以下內容:
為什麼需要EM演算法
EM演算法的推導與流程
EM演算法的收斂性定理
使用EM演算法求解三硬幣模型
為什麼需要EM演算法
數理統計的基本問題就是根據樣本所提供的資訊,對總體的分佈或者分佈的數字特徵作出統計推斷。所謂總體,就是一個具有確定分佈的隨機變數,來自總體的每一個iid樣本都是一個與總體有相同分佈的隨機變數。
引數估計是指這樣一類問題——總體所服從的分佈型別已知,但某些引數未知:設 Y1,...,YNY1,...,YN 是來自總體 YY 的iid樣本,記 Y=(y1,...,yN)Y=(y1,...,yN) 是樣本觀測值,如果隨機變數 Y1,...,YNY1,...,YN 是可觀測的,那麼直接用極大似然估計法就可以估計引數 θθ 。
但是,如果裡面含有不可觀測的隱變數,使用MLE就沒那麼容易。EM演算法正是服務於求解帶有隱變數的引數估計問題。
EM演算法的推導與流程
下面考慮帶有隱變數 ZZ (觀測值為 zz )的引數估計問題。將觀測資料(亦稱不完全資料)記為 Y=(y1,...,yN)Y=(y1,...,yN) ,不可觀測資料記為 Z=(z1,...,zN)Z=(z1,...,zN) , YY 、ZZ 合在一起稱為完全資料。那麼觀測資料的似然函式為
l(θ)=∏j=1NP(yj|θ)=∏j=1N∑zP(z|θ)P(yj|z,θ)l(θ)=∏j=1NP(yj|θ)=∏j=1N∑zP(z|θ)P(yj|z,θ)
其中求和號表示對 zz 的所有可能取值求和。
為了省事,表述成這個形式:
l(θ)=P(Y|θ)=∑zP(z|θ)P(Y|z,θ)l(θ)=P(Y|θ)=∑zP(z|θ)P(Y|z,θ)
對數似然:
L(θ)=lnP(Y|θ)=ln∑zP(z|θ)P(Y|z,θ)L(θ)=lnP(Y|θ)=ln∑zP(z|θ)P(Y|z,θ)
EM演算法是一種迭代演算法,通過迭代的方式求取目標函式 L(θ)=lnP(Y|θ)L(θ)=lnP(Y|θ) 的極大值。因此,希望每一步迭代之後的目標函式值會比上一步迭代結束之後的值大。設當前第 nn 次迭代後引數取值為 θnθn ,我們的目的是使 L(θn+1)>L(θn)L(θn+1)>L(θn) 。那麼考慮:
L(θ)−L(θn)=ln(∑zP(z|θ)P(Y|z,θ))−lnP(Y|θn)L(θ)−L(θn)=ln(∑zP(z|θ)P(Y|z,θ))−lnP(Y|θn)
使用Jensen不等式:
ln∑jλjyj≥∑jλjlogyj,λj≥0,∑jλj=1ln∑jλjyj≥∑jλjlogyj,λj≥0,∑jλj=1
因為 ∑zP(z|Y,θn)=1∑zP(z|Y,θn)=1 ,所以 L(θ)−L(θn)L(θ)−L(θn) 的第一項有
ln(∑zP(z|θ)P(Y|z,θ))=ln(∑zP(z|Y,θn)P(z|θ)P(Y|z,θ)P(z|Y,θn))≥∑zP(z|Y,θn)lnP(z|θ)P(Y|z,θ)P(z|Y,θn)ln(∑zP(z|θ)P(Y|z,θ))=ln(∑zP(z|Y,θn)P(z|θ)P(Y|z,θ)P(z|Y,θn))≥∑zP(z|Y,θn)lnP(z|θ)P(Y|z,θ)P(z|Y,θn)
第二項有
−lnP(Y|θn)=−∑zP(z|Y,θn)lnP(Y|θn)−lnP(Y|θn)=−∑zP(z|Y,θn)lnP(Y|θn)
則 L(θ)−L(θn)L(θ)−L(θn) 的下界為
L(θ)−L(θn)≥∑zP(z|Y,θn)lnP(z|θ)P(Y|z,θ)P(z|Y,θn)−∑zP(z|Y,θn)lnP(Y|θn)=∑z[P(z|Y,θn)lnP(z|θ)P(Y|z,θ)P(z|Y,θn)−P(z|Y,θn)lnP(Y|θn)]=∑zP(z|Y,θn)lnP(z|θ)P(Y|z,θ)P(Y|θn)P(z|Y,θn)L(θ)−L(θn)≥∑zP(z|Y,θn)lnP(z|θ)P(Y|z,θ)P(z|Y,θn)−∑zP(z|Y,θn)lnP(Y|θn)=∑z[P(z|Y,θn)lnP(z|θ)P(Y|z,θ)P(z|Y,θn)−P(z|Y,θn)lnP(Y|θn)]=∑zP(z|Y,θn)lnP(z|θ)P(Y|z,θ)P(Y|θn)P(z|Y,θn)
定義一個函式 l(θ|θn)l(θ|θn) :
l(θ|θn)≜L(θn)+∑zP(z|Y,θn)lnP(z|θ)P(Y|z,θ)P(Y|θn)P(z|Y,θn)l(θ|θn)≜L(θn)+∑zP(z|Y,θn)lnP(z|θ)P(Y|z,θ)P(Y|θn)P(z|Y,θn)
從而有 L(θ)≥l(θ|θn)L(θ)≥l(θ|θn) ,也就是說第 nn 次迭代結束後, L(θ)L(θ) 的一個下界為 l(θ|θn)l(θ|θn)。另外,有等式 L(θn)=l(θn|θn)L(θn)=l(θn|θn) 成立。
我們的目的是使下一次迭代後得到的目標函式值能夠大於當前的值: L(θn+1)>L(θn)L(θn+1)>L(θn),即 L(θn+1)>l(θn|θn)L(θn+1)>l(θn|θn) 。
而在當前, L(θ)L(θ) 的下界為 l(θ|θn)l(θ|θn) ,因此,任何能讓 l(θ|θn)l(θ|θn) 增大的 θθ ,也可以讓 L(θ)L(θ) 增大。
也就是說,能滿足 l(θn+1|θn)>l(θn|θn)l(θn+1|θn)>l(θn|θn) 的 θn+1θn+1 ,一定更能滿足L(θn+1)>l(θn|θn)=L(θn)L(θn+1)>l(θn|θn)=L(θn) 。
通過下圖(來源:參考資料[1],自己做了點註釋)可以解釋:
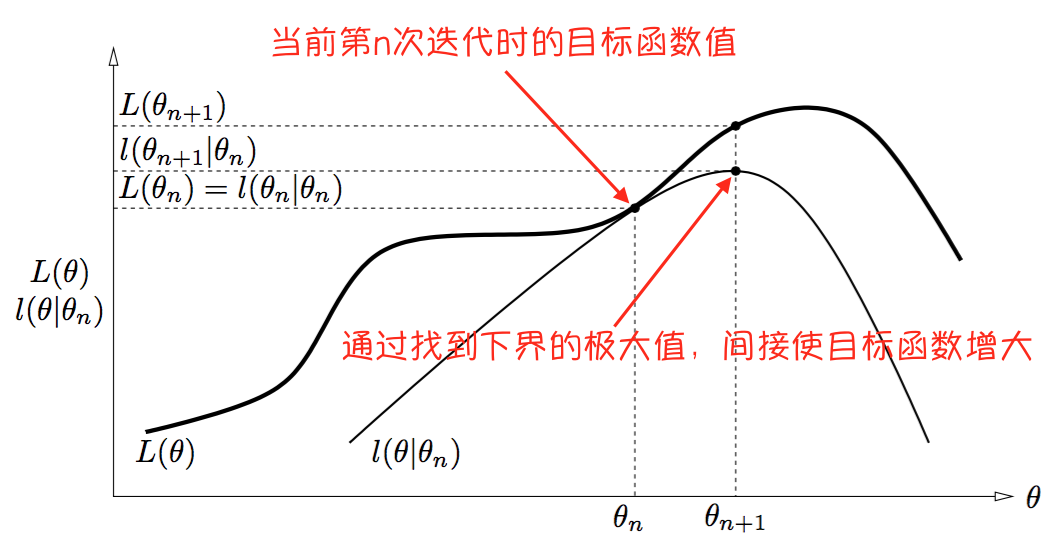
需要注意的是,下界的曲線當然是隨著迭代的進行而變化的:在第 ii 次迭代結束後,總是有不等式 L(θ)≥l(θ|θi)L(θ)≥l(θ|θi) 和等式 L(θi)=l(θi|θi)L(θi)=l(θi|θi) 成立。
換句話說,EM演算法通過優化對數似然在當前的下界,來間接優化對數似然。
ok,那麼現在問題就從找滿足 L(θn+1)>L(θn)L(θn+1)>L(θn) 的 θn+1θn+1 ,
轉變成了找滿足 l(θn+1|θn)>l(θn|θn)l(θn+1|θn)>l(θn|θn) 的 θn+1θn+1 。如何找到這樣一個 θn+1θn+1 ?直接找 l(θ|θn)l(θ|θn) 的最優解唄:
θn+1=argmaxθl(θ|θn)θn+1=argmaxθl(θ|θn)
把 l(θ|θn)l(θ|θn) 中的幾個與 θθ 無關的量去掉,從而有
θn+1=argmaxθ∑zP(z|Y,θn)ln[P(z|θ)P(Y|z,θ)]=argmaxθ∑zP(z|Y,θn)lnP(Y,z|θ)θn+1=argmaxθ∑zP(z|Y,θn)ln[P(z|θ)P(Y|z,θ)]=argmaxθ∑zP(z|Y,θn)lnP(Y,z|θ)
回顧一下隨機變數的期望的表示式:
E[Z]=∑kP(Z=zk)zkE[Z]=∑kP(Z=zk)zk
E[g(Z)]=∑kP(Z=zk)g(zk)E[g(Z)]=∑kP(Z=zk)g(zk)
E[Z|Y=y]=∑kP(Z=zk|Y=y)zkE[Z|Y=y]=∑kP(Z=zk|Y=y)zk
所以:
θn+1=argmaxθEZ|Y,θn[lnP(Y,z|θ)]=argmaxθQ(θ|θn)θn+1=argmaxθEZ|Y,θn[lnP(Y,z|θ)]=argmaxθQ(θ|θn)
上式定義了一個函式 Q(θ|θn)Q(θ|θn) ,稱為 QQ 函式。
上式完整表明了EM演算法中的一步迭代中所需要的兩個步驟:E-step,求期望;M-step,求極大值。有了上面的鋪墊,下面介紹EM演算法的流程:
輸入:觀測資料 YY ,不可觀測資料 ZZ;
輸出:引數 θθ ;
步驟:1. 給出引數初始化值 θ0θ0 ;
2. E步:記 θnθn 為第 nn 次迭代後引數的估計值。在第 n+1n+1 次迭代的E步,求期望( QQ 函式)
Q(θ|θn)=EZ|Y,θn[lnP(Y,z|θ)]=∑zP(z|Y,θn)lnP(Y,z|θ)Q(θ|θn)=EZ|Y,θn[lnP(Y,z|θ)]=∑zP(z|Y,θn)lnP(Y,z|θ)
3. M步:求 QQ 函式的極大值點,來作為第 n+1n+1 次迭代所得到的引數估計值 θn+1θn+1
θn+1=argmaxθQ(θ|θn)θn+1=argmaxθQ(θ|θn)
4. 重複上面兩步,直至達到停機條件。
EM演算法的收斂性定理
定理1:觀測資料的似然函式 P(Y|θ)P(Y|θ) 通過EM演算法得到的序列 P(Y|θn)(n=1,2,...)P(Y|θn)(n=1,2,...) 單調遞增:P(Y|θn+1)≥P(Y|θn)P(Y|θn+1)≥P(Y|θn) 。
定理2:(1) 如果 P(Y|θ)P(Y|θ) 有上界,則 L(θn)=lnP(Y|θn)L(θn)=lnP(Y|θn) 收斂到某一值 L∗L∗ ;
(2) 在 QQ 函式與 L(θ)L(θ) 滿足一定條件下,由EM演算法得到的引數估計序列 θnθn的收斂值 θ∗θ∗ 是 L(θ)L(θ) 的穩定點。
定理2中第二點的“條件”在大多數情況下都滿足。只能保證收斂到穩定點,不能保證收斂到極大值點,因此EM演算法受初值的影響較大。
使用EM演算法求解三硬幣模型
參考資料[2]給出了三硬幣模型的描述:
假設有三枚硬幣A、B、C,這些硬幣正面出現的概率分別是 ππ 、pp 、qq 。進行如下擲硬幣試驗:
先擲A,如果A是正面則再擲B,如果A是反面則再擲C。對於B或C的結果,如果是正面則記為1,如果是反面則記為0。進行 NN 次獨立重複實驗,得到結果。現在只能觀測到結果,不能觀測到擲硬幣的過程,估計模型引數 θ=(π,p,q)θ=(π,p,q) 。
在這個問題中,實驗結果是可觀測資料 Y=(y1,...,yn)Y=(y1,...,yn) ,硬幣A的結果是不可觀測資料 Z=(z1,...,zn)Z=(z1,...,zn) 且 zz 只有兩種可能取值1和0。
對於第 jj 次試驗,
P(yj|θ)=∑zP(yj,z|θ)=∑zP(z|θ)P(yj|z,θ)=P(z=1|θ)P(yj|z=1,θ)+P(z=0|θ)P(yj|z=0,θ)={πp+(1−π)q,π(1−p)+(1−π)(1−q),if yj=1;if yj=0.=πpyj(1−p)1−yj+(1−π)qyj(1−q)1−yjP(yj|θ)=∑zP(yj,z|θ)=∑zP(z|θ)P(yj|z,θ)=P(z=1|θ)P(yj|z=1,θ)+P(z=0|θ)P(yj|z=0,θ)={πp+(1−π)q,if yj=1;π(1−p)+(1−π)(1−q),if yj=0.=πpyj(1−p)1−yj+(1−π)qyj(1−q)1−yj
所以有
P(Y|θ)=∏j=1NP(yj|θ)=∏j=1N(πpyj(1−p)1−yj+(1−π)qyj(1−q)1−yj)P(Y|θ)=∏j=1NP(yj|θ)=∏j=1N(πpyj(1−p)1−yj+(1−π)qyj(1−q)1−yj)
1. E-step,求期望(Q函式):
Q(θ|θn)=∑zP(z|Y,θn)lnP(Y,z|θ)=∑j=1N{∑zP(z|yj,θn)lnP(yj,z|θ)}=∑j=1N{P(z=1|yj,θn)lnP(yj,z=1|θ)+P(z=0|yj,θn)lnP(yj,z=0|θ)}Q(θ|θn)=∑zP(z|Y,θn)lnP(Y,z|θ)=∑j=1N{∑zP(z|yj,θn)lnP(yj,z|θ)}=∑j=1N{P(z=1|yj,θn)lnP(yj,z=1|θ)+P(z=0|yj,θn)lnP(yj,z=0|θ)}
先求 P(z|yj,θn)P(z|yj,θn) ,
P(z|yj,θn)=⎧⎩⎨πnpyjn(1−pn)1−yjπnpyjn(1−pn)1−yj+(1−πn)qyjn(1−qn)1−yj=μj,n1−μj,nif z=1;if z=0.P(z|yj,θn)={πnpnyj(1−pn)1−yjπnpnyj(1−pn)1−yj+(1−πn)qnyj(1−qn)1−yj=μj,nif z=1;1−μj,nif z=0.
再求 P(yj,z|θ)=P(z|θ)P(yj|z,θ)P(yj,z|θ)=P(z|θ)P(yj|z,θ) ,
P(yj,z|θ)={πpyj(1−p)1−yj(1−π)qyj(1−q)1−yjif z=1;if z=0.P(yj,z|θ)={πpyj(1−p)1−yjif z=1;(1−π)qyj(1−q)1−yjif z=0.
因此,QQ 函式表示式為:
Q(θ|θn)=∑j=1N{μj,nln[πpyj(1−p)1−yj]+(1−μj,n)ln[(1−π)qyj(1−q)1−yj]}Q(θ|θn)=∑j=1N{μj,nln[πpyj(1−p)1−yj]+(1−μj,n)ln[(1−π)qyj(1−q)1−yj]}
2. M-step,求 QQ 函式的極大值:
令 QQ 函式對引數求導數,並等於零。
∂Q(θ|θn)∂π=∑j=1N{μj,nln[πpyj(1−p)1−yj]+(1−μj,n)ln[(1−π)qyj(1−q)1−yj]∂π}=∑j=1N{μj,npyj(1−p)1−yjπpyj(1−p)1−yj+(1−μj,n)−qyj(1−q)1−yj(1−π)qyj(1−q)1−yj}=∑j=1N{μj,n−ππ(1−π)}=(∑Nj=1μj,n)−nππ(1−π)∂Q(θ|θn)∂π=∑j=1N{μj,nln[πpyj(1−p)1−yj]+(1−μj,n)ln[(1−π)qyj(1−q)1−yj]∂π}=∑j=1N{μj,npyj(1−p)1−yjπpyj(1−p)1−yj+(1−μj,n)−qyj(1−q)1−yj(1−π)qyj(1−q)1−yj}=∑j=1N{μj,n−ππ(1−π)}=(∑j=1Nμj,n)−nππ(1−π)
∂Q(θ|θn)∂π=0∴πn+1⟹π=1n∑j=1Nμj,n=1n∑j=1Nμj,n∂Q(θ|θn)∂π=0⟹π=1n∑j=1Nμj,n∴πn+1=1n∑j=1Nμj,n
∂Q(θ|θn)∂p=∑j=1N{μj,nln[πpyj(1−p)1−yj]+(1−μj,n)ln[(1−π)qyj(1−q)1−yj]∂p}=∑j=1N{μj,nπ(yjpyj−1(1−p)1−yj+pyj(−1)(1−yj)(1−p)1−yj−1)πpyj(1−p)1−yj+0}=∑j=1N{μj,n(yj−p)p(1−p)}=(∑Nj=1μj,nyj)−(p∑Nj=1μj,n)p(1−p)∂Q(θ|θn)∂p=∑j=1N{μj,nln[πpyj(1−p)1−yj]+(1−μj,n)ln[(1−π)qyj(1−q)1−yj]∂p}=∑j=1N{μj,nπ(yjpyj−1(1−p)1−yj+pyj(−1)(1−yj)(1−p)1−yj−1)πpyj(1−p)1−yj+0}=∑j=1N{μj,n(yj−p)p(1−p)}=(∑j=1Nμj,nyj)−(p∑j=1Nμj,n)p(1−p)
∂Q(θ|θn)∂p=0∴pn+1qn+1⟹p=∑Nj=1μj,nyj∑Nj=1μj,n=∑Nj=1μj,nyj∑Nj=1μj,n=∑Nj=1(1−μj,n)yj∑Nj=1(1−μj,n)∂Q(θ|θn)∂p=0⟹p=∑j=1Nμj,nyj∑j=1Nμj,n∴pn+1=∑j=1Nμj,nyj∑j=1Nμj,nqn+1=∑j=1N(1−μj,n)yj∑j=1N(1−μj,n)
既然已經得到了三個引數的迭代式,便可給定初值,迭代求解了。
參考資料:
[1] The Expectation Maximization Algorithm: A short tutorial - Sean Borman
[2] 《統計學習方法》,李航
對於原創博文:如需轉載請註明出處http://www.cnblogs.com/Determined22/
