查詢(2)--動態查詢
動態查詢表:1.表結構本身是在查詢過程中動態生成的,即對於給定值 key ,若表中存在關鍵字等於 key 的記錄,則查詢成功返回;否則,插入關鍵字等於 key 的記錄。
2.動態查詢表主要有二叉樹結構和樹結構兩種型別。二叉樹結構有二叉排序樹、平衡二叉樹等。樹結構有B-樹、B+樹等。
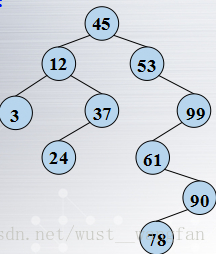
一.二叉排序樹:
1.定義:
1)若它的左子樹不空,則左子樹上所有結點的值均小於根結點的值;
2)若它的右子樹不空,則右子樹上所有結點的值均大於根結點的值;
3)它的左、右子樹也都分別是二叉排序樹。
2.儲存結構:
struct BtreeNode {
ElemType key; //關鍵字
BtreeNode *lchild, *rchild;//左、右孩子
} BtreeNode, *Bitree;(1)查詢:
BiTree SearchBST(BiTree T, KeyType key)
{
//若查詢成功,則返回指向該資料元素結點的指標
//否則返回空指標。
if ( (!T) || key = T-> data.key ) return(T);
else
if ( key < T-> data.key)
return(SearchBST (T-> lchild, key)); //在左子樹中繼續查詢
else
return(SearchBST (T-> rchild, key)); //在右子樹中繼續查詢
} // SearchBST
1) 若二叉排序樹為空樹,則新插入的結點為根結點;
2) 若二叉排序樹非空,則新插入的結點必為一個新的葉子結點,並且是查詢不成功時查詢路徑上訪問的最後一個結點的左孩子或右孩子結點。
Status SearchBST (BiTree T, KeyType key, BiTree f, BiTree &p )
{ //若查詢成功,則指標 p 指向該資料元素結點,並返回 TRUE
//否則指標 p 指向查詢路徑上訪問的最後一個結點,並返回 FALSE
//指標 f 指向 T 的雙親,其初始呼叫值為NULL。
if (!T) { p = f; return FALSE; } // 查詢不成功
else
if ( key = T-> data.key ) { p = T; return TRUE; } // 查詢成功
else
if ( key < T-> data.key )
SearchBST (T -> lchild, key, T, p ); // 在左子樹中查詢
else
SearchBST (T-> rchild, key, T, p ); // 在右子樹中查詢
} // SearchBST
Status InsertBST(BiTree &T, ElemType e )
{
// 當二叉排序樹 T 中不存在關鍵字等於 e.key 的資料元素時,
// 插入 e 並返回 TRUE,否則返回 FALSE
if (!SearchBST ( T, e.key,NULL,p))
{ // 查詢不成功
s = (BiTree) malloc (sizeof (BiTNode));
s -> data = e; s -> lchild = s -> rchild = NULL;
if ( !p ) T = s; // 插入 s 為新的根結點
else
if ( e.key < p -> data.key ) p -> lchild = s; // 插入 s 為左孩子
else p -> rchild = s; // 插入 s 為右孩子
return TRUE;
}
else
return FALSE; // 樹中已有關鍵字相同的結點,不再插入
} // Insert BST //反覆呼叫二叉排序樹的插入演算法即可
Bitree Creat (int n) {
//建立含有n個結點的二叉排序樹
Bitree T= NULL;
for ( int i=1; i<=n; i++)
{
cin>>x; //輸入關鍵字序列
InsertBST ( T, x);
}
return BST;
} 1)若*p結點為葉子結點,即PL和PR均為空樹。
由於刪去葉子結點不破壞整棵樹的結構,則只需修改其雙親結點的指標。
2)P只有左子樹或右子樹:
P只有左(右)子樹,用P的左(右)孩子代替P; 。
3)P左、右子樹均非空
用P的直接前驅(或直接後繼)取代P
4.二叉排序樹的查詢分析:
(1)含有 n 個結點的二叉排序樹的平均查詢長度和樹的形態有關
例如:
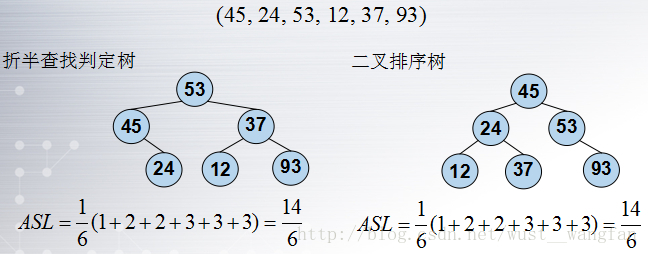
圖(1)
圖(2)
最好情況: ASL=
最壞情況:插入的 n 個元素從一開始就有序, 變成單支樹的形態! 此時樹的深度為 n;
A SL = (n + 1) / 2 ,查詢效率與順序查詢情況相同。
很明顯不同的二叉排序樹的ASL與形態有關!!!
實驗證明,二叉樹形態越均衡,ASL越短,那麼如何提高形態不均衡的二叉排序樹的查詢效率?引入平衡二叉樹。
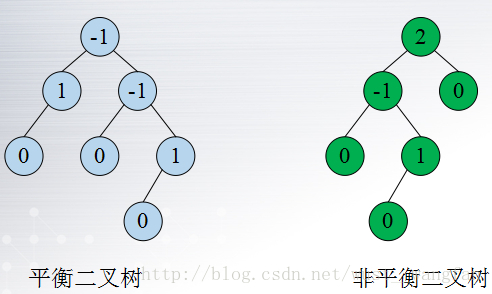
二.平衡二叉樹(AVL樹)
1.概念:|左子樹深度-右子樹深度| ≤ 1
其中-1,0,1為平衡因子,顯然AVL樹只能有這三個平衡因子!
2.平衡二叉樹的調整:
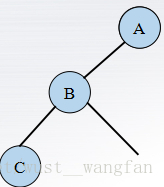
(1).LL平衡旋轉:若在 A 的左子樹的左子樹上插入
結點,使 A 的平衡因子從 1 增加
至 2, 需要進行一次順時針旋轉。 (以 B 為旋轉軸)
(2).RR 平衡旋轉:若在 A 的右子樹的右子樹上插入
結點,使 A 的平衡因子從 -1 改變
為 -2,需要進行一次逆時針旋轉。 (以 B 為旋轉軸)

(3) .LR平衡旋轉:若在 A 的左子樹的右子樹上插入
結點,使 A 的平衡因子從 1 增加
至 2, 需要先進行逆時針旋轉,
再順時針旋轉。 (以插入的結點 B 為旋轉軸)
(4).RL平衡旋轉:
若在 A 的右子樹的左子樹上插入
結點,使 A 的平衡因子從 -1 改變
為 -2,需要先進行順時針旋轉,再逆時針旋轉。(以插入的結點 B 為旋轉軸)
相關文章
- jpa動態查詢與多表聯合查詢
- 查詢(1)--靜態查詢
- ThinkPHP getBy動態查詢PHP
- SQL SERVER 動態查詢SQLServer
- Spring Data Jpa 的簡單查詢多表查詢HQL,SQL ,動態查詢, QueryDsl ,自定義查詢筆記SpringSQL筆記
- hibernate 動態查詢(DetachedCriteria )
- DS靜態查詢之順序查詢
- 查詢演算法集:順序查詢、二分查詢、插值查詢、動態查詢(陣列實現、連結串列實現)演算法陣列
- SQL查詢的:子查詢和多表查詢SQL
- XML卷之實戰錦囊(2)動態查詢(轉)XML
- PHP--動態生成sql查詢表格PHPSQL
- SpringDataJpa (二)-動態查詢&多表操作Spring
- web後端動態匹配模型查詢Web後端模型
- django 動態查詢實現過程Django
- 動態SQL——構造通用動態頁面查詢SQL
- 查詢之折半查詢
- mysql-分組查詢-子查詢-連線查詢-組合查詢MySql
- oracle狀態查詢(補)Oracle
- oracle常用狀態查詢Oracle
- 查詢網路狀態
- 複雜查詢—子查詢
- 查詢——二分查詢
- 子查詢-表子查詢
- Spring data jpa 多表查詢(三:多對多關係動態條件查詢)Spring
- MYSQL學習筆記25: 多表查詢(子查詢)[標量子查詢,列子查詢]MySql筆記
- Sy.ExpressionBuilder 動態查詢新體驗ExpressUI
- 資料庫 - 連線查詢、巢狀查詢、集合查詢資料庫巢狀
- 離線查詢與線上查詢
- 【SQL查詢】集合查詢之INTERSECTSQL
- 查詢與排序02,折半查詢排序
- Linq to Sql : 動態構造Expression進行動態查詢SQLExpress
- 靜態方法查詢類名
- 查詢
- #查詢演算法#【1】簡單查詢:順序、折半查詢演算法
- 一句SQL完成動態分級查詢SQL
- Laravel 通過子查詢建立動態關聯Laravel
- 如何完成複雜查詢的動態構建?
- linq to sql的多條件動態查詢SQL