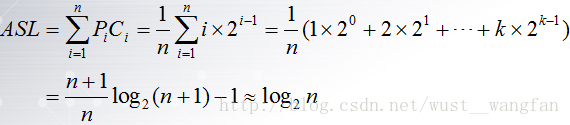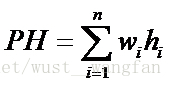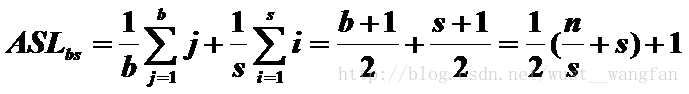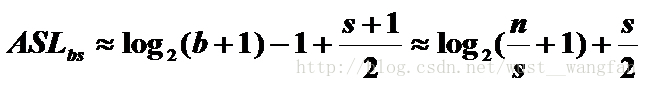查詢(1)--靜態查詢
查詢分為兩種:
靜態查詢: 只查詢,不改變資料元素集內的資料元素;
動態查詢:既查詢,又改變(增減)集合內的資料元素。
靜態查詢又分為三種:順序查詢,折半查詢,索引順序查詢(分塊查詢)
關鍵字:在實際應用問題中,每個記錄一般包含有多個資料域,查詢是根據其中某一個指定的域進行的,這個作為查詢依據的域稱關鍵字(key)。
主關鍵字: 可唯一標識一個記錄的關鍵字。例:學號
次關鍵字:可識別若干記錄的關鍵字。例:性別
一.順序查詢:
1.思想:從表的一端開始,逐個進行記錄的關鍵 字和給定值的比較。
2.演算法實現:
int SearchSeq(SSTable ST[],int n,int key)
{
int i=n;
while(ST[i].key!=key)&&(i>=0) i--;
return i;
}int SearchSeq(SSTable ST[],int n,int key)
{
ST[0].key=key;//避免每次比較的時候都要判斷是否查詢結束,設定一個監視哨
int i=n;
while(ST[i].key!=key)i--;
return i;
}3.ASL(平均查詢長度:表示找到相應的關鍵字預計比較的次數)
ASL=
(1) 查詢成功時的ASL=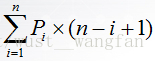
(2)查詢不成功的比較次數ASL=n+1次
所以順序查詢的平均查詢長度為(1)+(2)/2=3(n+1)/4
4.演算法優缺點分析:
優點:演算法簡單,無需排序,採用順序和鏈式儲存均可。
缺點:當n很大時,平均查詢長度較大。
二.折半查詢:
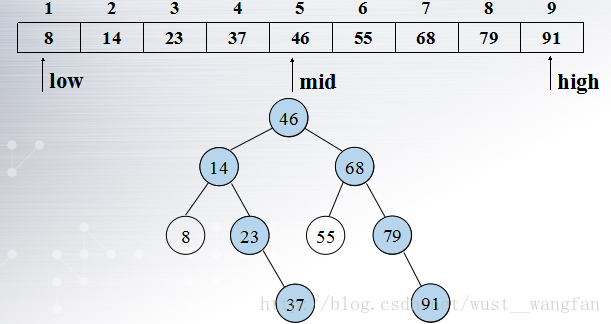
1.演算法思想:把靜態查詢表分為一個區間,每次都用關鍵字key和區間中間的一個元素(low+high)/2=mid相比,
如果相等,則返回結果; 如果key>SSTable[mid],low=mid+1,在右半部分找; 如果key<SSTable[mid],high=low-1,在左半部分找。
2.程式碼實現:
int Search_Bin( SSTable ST[ ], int n, int key)
{
int low, high,mid;
low=1; high=n;
while(low<=high) {
mid=(low+high)/2;
if (ST[mid].key == key) return mid;
else if ( key< ST[mid].key) high=mid-1;
else low=mid+1;
}
return 0;
}3.ASL分析:
(1)二分查詢判定樹:把當前查詢區間的中點作為根結點,左子區間和右子區間分別作為根的左子樹和右子樹,左子區間和右子區間再按類似的方法。
查詢成功:
*比較次數=二叉樹結點數=二叉樹深度
比較次數<=樹的深度(└ log2n ┘ + 1(向下取整))
查詢不成功:
比較次數<=樹的深度(└ log2n ┘ + 1(向下取整))
(2) 若在樹的高度為k的滿二叉樹n=2k-1中,樹的第i層有2i-1個結點,樹的第i層結點的全部查詢次數為i*2i-1,在等概率的情況下,Pi=1/n,因此,折半查詢的平均查 找長度為
4.優缺點分析:
優點:對於有序表查詢速度很快;
缺點:只適用於有序,順序儲存,並且元素改動的少的查詢表。
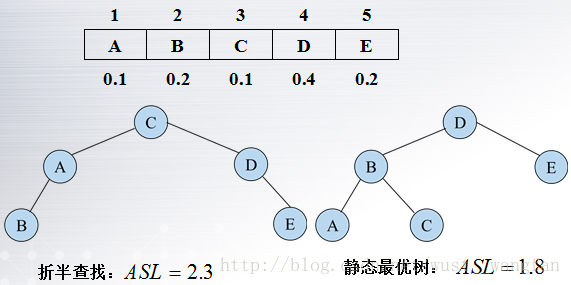
我們可以通過舉例證明當上述有序表的各個元素查詢的概率不同的時候,折半查詢的ASL並不是最優的,從而引出第三種查詢演算法。
三.靜態樹表的查詢:
1.靜態最優查詢樹(類似於哈夫曼樹)
若只考慮查詢成功的情況,則使查詢效能達最佳的判定樹是其帶權內路徑長度之和PH值取最小值的二叉樹。
其中:n為二叉樹上結點的個數(即有序表的長度);hi為第i個結點在二叉樹上的層次數;結點的權wi=cpi(i=1,2,…,n),其中pi為結點的查詢概率,c為某個常 量。稱PH值取最小的二叉樹為靜態最優查詢樹(Static Optimal Search Tree)
由於構造靜態最優查詢樹花費的時間代價較高,因此需要構造近似最優查詢樹的有效演算法
2.次優查詢樹(近似最優查詢樹)
構造次優查詢樹方法:
當資料很多時,順序查詢費時;折半查詢需要對元素先排序,也很費時,這時就需要一種折中的演算法了。
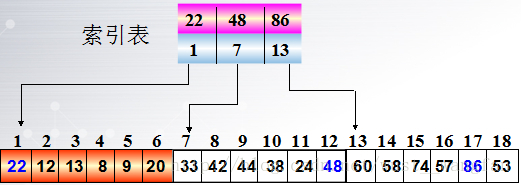
四.索引順序表的查詢(分塊查詢):
1.演算法思想:
把全部元素分成若干塊,塊內之間的元素不需要排序,然後另外開闢一個索引表來存放每個塊內的最大關鍵字和每個塊內的元素開始標號,當要查詢某個元素時,
先查詢塊號(折半或順序查詢),再根據開始標號在那個塊中順序查詢。
2.ASL分析:
平均查詢長度: ASLbs= Lb + Lw (Lb表示塊查詢長度,Lw表示塊內查詢長度)
若將長度為 n 的表均分成 b 塊,每塊含 s 個記錄 (b = n/s(向下取整)); 並設表中每個記錄的查詢概率相等,則每塊查詢的概率為 1/b, 塊中每個記錄的 查詢概率為 1/s。
(1)順序查詢塊號,順序查詢塊內元素:
(2).折半查詢塊號,順序查詢塊內元素:
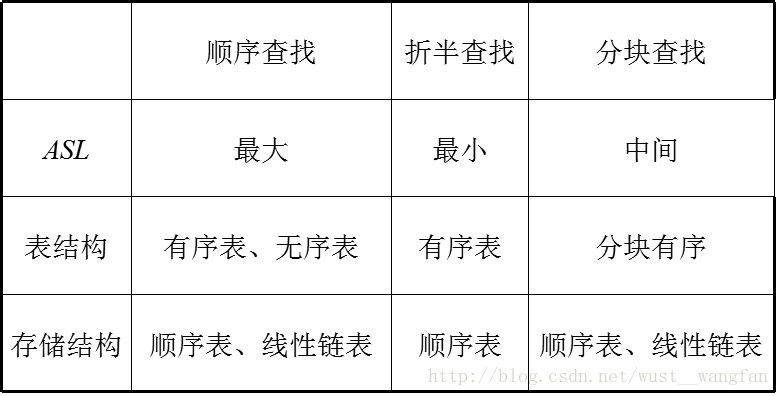
總結:
相關文章
- DS靜態查詢之順序查詢
- 靜態方法查詢類名
- 查詢(2)--動態查詢
- 【筆記】靜態查詢演算法筆記演算法
- #查詢演算法#【1】簡單查詢:順序、折半查詢演算法
- jpa動態查詢與多表聯合查詢
- Spring Data Jpa 的簡單查詢多表查詢HQL,SQL ,動態查詢, QueryDsl ,自定義查詢筆記SpringSQL筆記
- 一種期望線性的靜態區間查詢
- SQL查詢的:子查詢和多表查詢SQL
- (1)SQL 基本查詢SQL
- 常用SQL查詢1SQL
- 閃回查詢(1)
- 查詢演算法集:順序查詢、二分查詢、插值查詢、動態查詢(陣列實現、連結串列實現)演算法陣列
- 查詢之折半查詢
- mysql-分組查詢-子查詢-連線查詢-組合查詢MySql
- ThinkPHP getBy動態查詢PHP
- oracle狀態查詢(補)Oracle
- oracle常用狀態查詢Oracle
- 查詢網路狀態
- SQL SERVER 動態查詢SQLServer
- 複雜查詢—子查詢
- 查詢——二分查詢
- 子查詢-表子查詢
- PLSQL Language Referenc-PL/SQL靜態SQL-帶有子查詢的查詢結果集處理SQL
- MYSQL學習筆記25: 多表查詢(子查詢)[標量子查詢,列子查詢]MySql筆記
- 資料庫 - 連線查詢、巢狀查詢、集合查詢資料庫巢狀
- 離線查詢與線上查詢
- 【SQL查詢】集合查詢之INTERSECTSQL
- 查詢與排序02,折半查詢排序
- hibernate 動態查詢(DetachedCriteria )
- 查詢
- 實踐006-elasticsearch查詢之1-URI Search查詢Elasticsearch
- 五大經典查詢(1)_二叉排序樹查詢排序
- oracle 精確查詢和模糊查詢Oracle
- 查詢演算法__插值查詢演算法
- pgsql查詢優化之模糊查詢SQL優化
- MySQL - 資料查詢 - 簡單查詢MySql
- Elasticsearch複合查詢——boosting查詢Elasticsearch