資料結構與演算法面試題80道

題目來源“資料結構與演算法面試題80道”。這是第一部分，包含其中的第1題到第5題。 
在此給出我的解法，如你有更好的解法，歡迎留言。

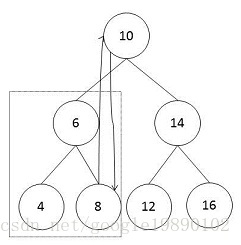
問題分析：二叉查詢樹是一種二叉樹的結構，其中，根節點的值大於左子樹的值，小於右子樹的值。而二叉查詢樹的中序遍歷即為排序的結果。對於根節點，前驅指標指向左子樹中最大的節點，同理，後驅指標指向右子樹中最小的節點，如下圖所示：

樹是一種遞迴的結果，因此，對於左右子樹，也需要執行相同的操作。

方法：

BSTreeNode* convert(BSTreeNode *root){
    if (NULL == root ||
        (NULL == root->m_pLeft && NULL == root->m_pRight)){
        return root;
    }

    convert(root->m_pLeft);
    BSTreeNode* p_left = root->m_pLeft;
    while(p_left->m_pRight != NULL){
        p_left = p_left->m_pRight;
    }
    root->m_pLeft = p_left;
    p_left->m_pRight = root;

    convert(root->m_pRight);
    BSTreeNode* p_right = root->m_pRight;
    while(p_right->m_pLeft != NULL){
        p_right = p_right->m_pLeft;
    }
    root->m_pRight = p_right;
    p_right->m_pLeft = root;

    BSTreeNode *p = root;
    while (NULL != p->m_pLeft){
        p = p->m_pLeft;
    }
    return p;
}

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28

問題分析：棧的特點是先進後出。要能夠取出當前的最小值，需要用另一個棧儲存當前的最小值，所以可採用“雙棧”的結構，一個棧儲存所有的值，另一個棧儲存當前的最小值。

方法：

template <class Type> class min_stack{
    private:
        stack<Type> s1;
        stack<Type> s2;
    public:
        min_stack(){}
        ~min_stack(){}

        Type min(){
            if (!s2.empty()){
                return s2.top();
            }
        }

        void push(Type a){
            s1.push(a);
            if (s2.empty() || a <= s2.top()){
                s2.push(a);
            }
        }

        Type pop(){
            if (!s1.empty() && !s2.empty()){// 非空
                if (s1.top() == s2.top()){
                    s2.pop();
                }
                return s1.pop();
            }
        }
};

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30

問題分析：在陣列的每一個位置處儲存當前的最大值，當前的最大值組成為：

解決方案：

int get_max_subarray(int *a, int length, bool &is_array_ok){
    if (NULL == a || length <= 0){
        is_array_ok = false;
        return 0;
    }

    int *p_h_a = (int *)malloc(sizeof(int) * length);
    // 遍歷陣列
    int max_num = 0;
    for (int i = 0; i < length; i++){
        if (i == 0 || (i > 0 && p_h_a[i-1] <= 0)){
            p_h_a[i] = a[i];
        }else{
            p_h_a[i] = p_h_a[i-1] + a[i];
        }
        if (max_num < p_h_a[i]) max_num = p_h_a[i];
    }
    free(p_h_a);

    is_array_ok = true;
    return max_num;
}

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22

問題分析：核心是樹的遍歷，注意題目中“路徑”的定義，是從根節點到葉子節點。先序遍歷正好是從根節點開始，因此可以利用先序遍歷的過程來實現這個過程。

方法：

void print_vector(vector<BinaryTreeNode *> &v){
    vector<BinaryTreeNode *>::iterator it;
    for (it = v.begin(); it != v.end(); it ++){
        printf("%d\t", (*it)->m_nValue);
    }
    printf("\n");
}

void pre_order_route(BinaryTreeNode *p, int num, vector<BinaryTreeNode *> &q, int &current){
    if (NULL == p) return;

    current += p->m_nValue;
    q.push_back(p);

    bool is_leaf = (NULL == p->m_pLeft) && (NULL == p->m_pRight);

    if (current == num && is_leaf){
        print_vector(q);
    }

    if (NULL != p->m_pLeft){
        pre_order_route(p->m_pLeft, num, q, current);
    }

    if (NULL != p->m_pRight){
        pre_order_route(p->m_pRight, num, q, current);
    }

    current -= (*(q.end() - 1))->m_nValue;
    q.pop_back();
}


void print_route(BinaryTreeNode *root, int num){
    vector<BinaryTreeNode *> q;// 用佇列儲存已經訪問過的節點
    int current = 0;
    pre_order_route(root, num, q, current);
}

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38

問題分析：這是一道比較經典的題目，查詢最小的k個元素，最簡單的方法就是對這n個整數排序，排序完成後，直接輸出前k個最小的元素。那麼最快的排序方法是快速排序，其演算法的時間複雜度為O(nlogn)。是否還存在比這個更快的方法呢？

方法一：利用快速排序的思想，時間複雜度為O(n)

按照某個點將陣列劃分成左右兩部分，左邊的數都小於該劃分節點，右邊的數都大於該劃分節點。如果最終該劃分節點的位置小於k-1，則在右邊節點中繼續劃分；如果最終該劃分節點的位置大於k-1，則在左邊節點中繼續劃分。這個過程直到最終的劃分節點的位置正好為k-1。

int swap(int *a, int start, int end, int point_index){
    int par_point = a[point_index];
    while (start < end){
        if (a[start] >= par_point && a[end] <= par_point){
            int tmp = a[start];
            a[start] = a[end];
            a[end] = tmp;
            start ++;
            end --;
        }else if(a[start] < par_point){
            start ++;
        }else{
            end --;
        }
    }
    return start;
}

void get_min_k(int *a, int length, int k){
    if (k > length || NULL == a || length <= 0) return;

    int new_index = swap(a, 0, length-1, k);
    while (true){
        if (new_index == k-1) break;
        else if (new_index > k-1){
            new_index = swap(a, 0, new_index-1, k);
        }else{
            new_index = swap(a, new_index+1, length-1, k);
        }
    }
}

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31

方法二：利用堆排序，時間複雜度為O(nlogk)

上述方法的缺點是其對陣列進行了修改，在堆排序中，可採用小頂堆，其中堆的大小為k，若此時堆的大小小於k時，則將數插入堆中；若此時堆中的大小大於等於k，則比較堆中最大的整數與待插入整數的大小，插入較小的整數。

void get_min_k(int *a, int length, int k, set<int> &s){
    if (k > length || NULL == a || length <= 0) return;

    for (int i = 0; i < length; i++){
        if (s.size() < k){
            s.insert(a[i]);
        }else{
            set<int>::iterator it = --s.end();
            if (a[i] < *it){
                s.erase(*it);
                s.insert(a[i]);
            }
        }
    }
}

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15