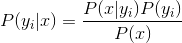Spark MLlib NaiveBayes 貝葉斯分類器

1.1樸素貝葉斯公式

貝葉斯定理：

      

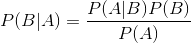
其中A為事件，B為類別，P(B|A)為事件A條件下屬於B類別的概率。

樸素貝葉斯分類的正式定義如下：

      1、設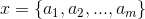為一個待分類項，而每個a為x的一個特徵屬性。

      2、有類別集合。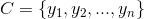

      3、計算。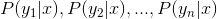

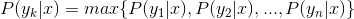
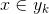
      4、如果，則 。

      那麼現在的關鍵就是如何計算第3步中的各個條件概率：

      1、找到一個已知分類的待分類項集合，這個集合叫做訓練樣本集。

      2、統計得到在各類別下各個特徵屬性的條件概率估計。即 。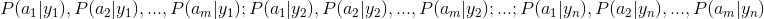

      3、如果各個特徵屬性是條件獨立的，則根據貝葉斯定理有如下推導：

      

      因為分母對於所有類別為常數，因為我們只要將分子最大化皆可。又因為各特徵屬性是條件獨立的，所以有：

        

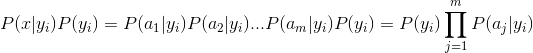
1.2 NaiveBayesModel原始碼解析

1、NaiveBayesModel主要的三個變數：

1）labels：類別

scala> labels

res56: Array[Double] = Array(2.0, 0.0, 1.0)

2）pi：各個label的先驗概率

scala> pi

res57: Array[Double] = Array(-1.1631508098056809, -0.9808292530117262, -1.1631508098056809)

3）theta：儲存各個特徵在各個類別中的條件概率。

scala> theta

res58: Array[Array[Double]] = Array(Array(-2.032921526044943, -1.8658674413817768, -0.33647223662121295), Array(-0.2451224580329847, -2.179982770901713, -2.26002547857525), Array(-1.9676501356917193, -0.28410425110389714, -2.2300144001592104))

4）lambda：平滑因子

 

2、NaiveBayesModel程式碼

1) train

/**

   * Run the algorithm with the configured parameters on an input RDD of LabeledPoint entries.

   *

   * @param data RDD of [[org.apache.spark.mllib.regression.LabeledPoint]].

   */

  def run(data: RDD[LabeledPoint]) = {

// requireNonnegativeValues：取每一個樣本資料的特徵值，以向量形式儲存，特徵植必需為非負數。

    val requireNonnegativeValues: Vector => Unit = (v: Vector) => {

      val values = vmatch {

        case SparseVector(size, indices, values) =>

          values

        case DenseVector(values) =>

          values

      }

      if (!values.forall(_ >=0.0)) {

        thrownew SparkException(s"Naive Bayes requires nonnegative feature values but found $v.")

      }

    }

 

    // Aggregates term frequencies per label.

    // TODO: Calling combineByKey and collect creates two stages, we can implement something

// TODO: similar to reduceByKeyLocally to save one stage.

// aggregated：對所有樣本資料進行聚合，以label為key，聚合同一個label的features；

// createCombiner：完成樣本從V到C的combine轉換，(v: Vector) –> (c: (Long, BDV[Double])

// mergeValue：將下一個樣本中Value合併為操作後的C型別資料，(c: (Long, BDV[Double]), v: Vector) –> (c: (Long, BDV[Double])；

// mergeCombiners：根據每個Key所對應的多個C，進行歸併，(c1: (Long, BDV[Double]), c2: (Long, BDV[Double])) –> (c: (Long, BDV[Double])；

    val aggregated = data.map(p => (p.label, p.features)).combineByKey[(Long, BDV[Double])](

      createCombiner = (v: Vector) => {

        requireNonnegativeValues(v)

        (1L, v.toBreeze.toDenseVector)

      },

      mergeValue = (c: (Long, BDV[Double]), v: Vector) => {

        requireNonnegativeValues(v)

        (c._1 + 1L, c._2 += v.toBreeze)

      },

      mergeCombiners = (c1: (Long, BDV[Double]), c2: (Long, BDV[Double])) =>

        (c1._1 + c2._1, c1._2 += c2._2)

    ).collect()

    val numLabels = aggregated.length

    var numDocuments =0L

    aggregated.foreach { case (_, (n, _)) =>

      numDocuments += n

    }

    val numFeatures = aggregated.headmatch {case (_, (_, v)) => v.size }

    val labels =new Array[Double](numLabels)

    val pi =new Array[Double](numLabels)

    val theta = Array.fill(numLabels)(new Array[Double](numFeatures))

    val piLogDenom = math.log(numDocuments + numLabels * lambda)

var i =0

// labels：儲存類別

// pi：計算每個類別的概率

// theta：計算在該類別下每個特徵的概率

    aggregated.foreach { case (label, (n, sumTermFreqs)) =>

      labels(i) = label

      val thetaLogDenom = math.log(brzSum(sumTermFreqs) + numFeatures * lambda)

      pi(i) = math.log(n + lambda) - piLogDenom

      var j =0

      while (j < numFeatures) {

        theta(i)(j) = math.log(sumTermFreqs(j) + lambda) - thetaLogDenom

        j += 1

      }

      i += 1

    }

// 返回模型

    new NaiveBayesModel(labels, pi, theta)

  }

 

2) predict

// brzPi各類別概率向量，brzTheta每個類別下各特徵概率矩陣

privateval brzPi =new BDV[Double](pi)

  privateval brzTheta =new BDM[Double](theta.length, theta(0).length)

 

  {

    // Need to put an extra pair of braces to prevent Scala treating `i` as a member.

    var i =0

    while (i < theta.length) {

      var j =0

      while (j < theta(i).length) {

        brzTheta(i, j) = theta(i)(j)

        j += 1

      }

      i += 1

    }

  }

// 根據各類別概率向量，每個類別下各特徵概率矩陣，對樣本RDD計算，其中對每行向量資料進行計算。

  overridedef predict(testData: RDD[Vector]): RDD[Double] = {

    val bcModel = testData.context.broadcast(this)

    testData.mapPartitions { iter =>

      val model = bcModel.value

      iter.map(model.predict)

    }

  }

// 根據各類別概率向量，每個類別下各特徵概率矩陣，對測試向量資料進行計算。

  overridedef predict(testData: Vector): Double = {

    labels(brzArgmax(brzPi + brzTheta * testData.toBreeze))

  }

計算過程如下：

測試樣本：0.0,[1.0,0.0,0.1]

scala> labels

res87: Array[Double] = Array(2.0, 0.0, 1.0)

 

scala> pi

res76: Array[Double] = Array(-1.1631508098056809, -0.9808292530117262, -1.1631508098056809)

 

scala> theta

res77: Array[Array[Double]] = Array(Array(-2.032921526044943, -1.8658674413817768, -0.33647223662121295), Array(-0.2451224580329847, -2.179982770901713, -2.26002547857525), Array(-1.9676501356917193, -0.28410425110389714, -2.2300144001592104))

 

scala> brzPi

res78: breeze.linalg.DenseVector[Double] = DenseVector(-1.1631508098056809, -0.9808292530117262, -1.1631508098056809)

 

scala> brzTheta

res79: breeze.linalg.DenseMatrix[Double] =

-2.032921526044943   -1.8658674413817768   -0.33647223662121295 

-0.2451224580329847  -2.179982770901713    -2.26002547857525    

-1.9676501356917193  -0.28410425110389714  -2.2300144001592104  

 

scala> val testData = new BDV[Double](Array(1.0,0.0,0.1))

testData: breeze.linalg.DenseVector[Double] = DenseVector(1.0, 0.0, 0.1)

 

scala> brzPi + brzTheta * testData

res86: breeze.linalg.DenseVector[Double] = DenseVector(-3.2297195595127457, -1.4519542589022358, -3.3538023855133217)

 

scala> labels(brzArgmax(brzPi + brzTheta * testData))

res88: Double = 0.0

結果正確。

1.3 NaiveBayesModel例項

1、資料

資料格式為：類別, 特徵1 特徵2 特徵3

0,1 0 0

0,2 0 0

0,1 0 0.1

0,2 0 0.2

0,1 0.1 0

0,2 0.2 0

1,0 1 0.1

1,0 2 0.2

1,0.1 1 0

1,0.2 2 0

1,0 1 0

1,0 2 0

2,0.1 0 1

2,0.2 0 2

2,0 0.1 1

2,0 0.2 2

2,0 0 1

2,0 0 2

2、程式碼

//資料路徑

valdata_path ="user/tmp/sample_naive_bayes_data.txt"

//讀取資料，轉換成LabeledPoint型別

    valexamples =sc.textFile(data_path).map { line =>

      valitems =line.split(',')

      vallabel =items(0).toDouble

      valvalue =items(1).split(' ').toArray.map(f =>f.toDouble)

      LabeledPoint(label, Vectors.dense(value))

    }

examples.cache()

//樣本劃分，80%訓練，20%測試

    valsplits =examples.randomSplit(Array(0.8,0.2))

    valtraining =splits(0)

    valtest =splits(1)

    valnumTraining =training.count()

    valnumTest =test.count()

    println(s"numTraining = $numTraining, numTest = $numTest.")

//樣本訓練，生成分類模型

    valmodel =new NaiveBayes().setLambda(1.0).run(training)

//根據分類模型，對測試資料進行測試，計算測試資料的正常率

    valprediction =model.predict(test.map(_.features))

    valpredictionAndLabel =prediction.zip(test.map(_.label))

    valaccuracy =predictionAndLabel.filter(x => x._1 == x._2).count().toDouble /numTest

    println(s"Test accuracy = $accuracy.")