十種排序演算法總結(冒泡、插入、選擇、希爾、歸併、堆、快速,計數,桶,基數)
http://blog.csdn.net/jnu_simba/article/details/9705111
首先宣告一下,本文只對十種排序演算法做簡單總結,並參照一些資料給出自己的程式碼實現,並沒有對某種演算法理論講解,更詳細的
瞭解可以參考以下資料(本人蔘考):
1、《data structure and algorithm analysis in c 》
2、《大話資料結構》
3、http://blog.csdn.net/morewindows/article/details/7961256
4、http://www.cs.usfca.edu/~galles/visualization/Algorithms.html
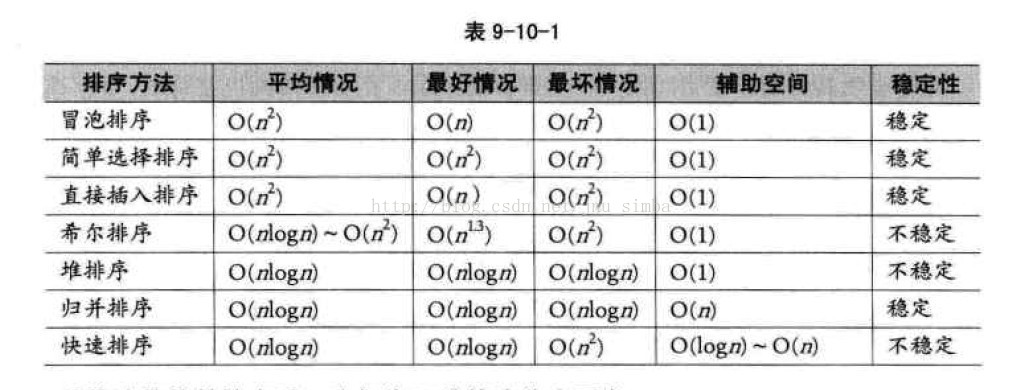
一、氣泡排序
基本思想是:兩兩比較相鄰記錄的關鍵字,如果反序則交換
氣泡排序時間複雜度最好的情況為O(n),最壞的情況是O(n^2)
改進思路1:設定標誌位,明顯如果有一趟沒有發生交換(flag = false),說明排序已經完成
改進思路2:記錄一輪下來標記的最後位置,下次從頭部遍歷到這個位置就Ok
二、直接插入排序
將一個記錄插入到已經排好序的有序表中, 從而得到一個新的,記錄數增1的有序表
時間複雜度也為O(n^2), 比冒泡法和選擇排序的效能要更好一些
三、簡單選擇排序
通過n-i次關鍵字之間的比較,從n-i+1 個記錄中選擇關鍵字最小的記錄,並和第i(1<=i<=n)個記錄交換之
儘管與氣泡排序同為O(n^2),但簡單選擇排序的效能要略優於氣泡排序
四、希爾排序
先將整個待排元素序列分割成若干子序列(由相隔某個“增量”的元素組成的)分別進行直接插入排序,然後依次縮減增量再進行排
序,待整個序列中的元素基本有序(增量足夠小)時,再對全體元素進行一次直接插入排序(增量為1)。其時間複雜度為O(n^3/2),要好於直接
插入排序的O(n^2)
五、歸併排序
假設初始序列含有n個記錄,則可以看成n個有序的子序列,每個子序列的長度為1,然後兩兩歸併,得到(不小於n/2的最小整數)個長度為2
或1的有序子序列,再兩兩歸併,...如此重複,直至得到一個長度為n的有序序列為止,這種排序方法稱為2路歸併排序。 時間複雜度為
O(nlogn),空間複雜度為O(n+logn),如果非遞迴實現歸併,則避免了遞迴時深度為logn的棧空間 空間複雜度為O(n)
六、堆排序
堆是具有下列性質的完全二叉樹:每個節點的值都大於或等於其左右孩子節點的值,稱為大頂堆;或者每個節點的值都小於或等於其左
右孩子節點的值,稱為小頂堆。
堆排序就是利用堆進行排序的方法.基本思想是:將待排序的序列構造成一個大頂堆.此時,整個序列的最大值就是堆頂 的根結點.將它移
走(其實就是將其與堆陣列的末尾元素交換, 此時末尾元素就是最大值),然後將剩餘的n-1個序列重新構造成一個堆,這樣就會得到n個元
素的次大值.如此反覆執行,便能得到一個有序序列了。 時間複雜度為 O(nlogn),好於冒泡,簡單選擇,直接插入的O(n^2)
七、快速排序
通過一趟排序將要排序的資料分割成獨立的兩部分,其中一部分的所有資料都比另外一部分的所有資料都要小,然後再按此方法對這兩部分資料分別進行快速排序,整個排序過程可以遞迴進行,以此達到整個資料變成有序序列。時間複雜度為O(nlogn)
下文沒有給出快速排序的實現,參考以前的文章。
程式碼實現:(含3種swap交換函式,6個排序演算法,不含快速排序)
|
1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 |
#include<iostream> using namespace std; void swap1(int *left, int *right) { int temp = *left; *left = *right; *right = temp; } void swap2(int &left, int &right) { int temp = left; left = right; right = left; } void swap3(int &left, int &right) { if (&left != &right) { left ^= right; right ^= left; left ^= right; } } /*****************************************************************/ /* 氣泡排序時間複雜度最好的情況為O(n),最壞的情況是O(n^2) * 基本思想是:兩兩比較相鄰記錄的關鍵字,如果反序則交換 */ void BubbleSort1(int arr[], int num) { int i, j; for (i = 0; i < num; i++) { for (j = 1; j < num - i; j++) { if (arr[j - 1] > arr[j]) swap1(&arr[j - 1], &arr[j]); } } } // 改進思路:設定標誌位,明顯如果有一趟沒有發生交換(flag = flase),說明排序已經完成. void BubbleSort2(int arr[], int num) { int k = num; int j; bool flag = true; while (flag) { flag = false; for (j = 1; j < k; j++) { if (arr[j - 1] > arr[j]) { swap1(&arr[j - 1], &arr[j]); flag = true; } } k--; } } //改進思路:記錄一輪下來標記的最後位置,下次從頭部遍歷到這個位置就Ok void BubbleSort3(int arr[], int num) { int k, j; int flag = num; while (flag > 0) { k = flag; flag = 0; for (j = 1; j < k; j++) { if (arr[j - 1] > arr[j]) { swap1(&arr[j - 1], &arr[j]); flag = j; } } } } /*************************************************************************/ /**************************************************************************/ /*插入排序: 將一個記錄插入到已經排好序的有序表中, 從而得到一個新的,記錄數增1的有序表 * 時間複雜度也為O(n^2), 比冒泡法和選擇排序的效能要更好一些 */ void InsertionSort(int arr[], int num) { int temp; int i, j; for (i = 1; i < num; i++) { temp = arr[i]; for (j = i; j > 0 && arr[j - 1] > temp; j--) arr[j] = arr[j - 1]; arr[j] = temp; } } /****************************************************************************/ /*希爾排序:先將整個待排元素序列分割成若干子序列(由相隔某個“增量”的元素組成的)分別進行 直接插入排序,然後依次縮減增量再進行排序,待整個序列中的元素基本有序(增量足夠小)時, 再對全體元素進行一次直接插入排序(增量為1)。其時間複雜度為O(n^3/2),要好於直接插入排序的O(n^2) */ void ShellSort(int *arr, int N) { int i, j, increment; int tmp; for (increment = N / 2; increment > 0; increment /= 2) { for (i = increment; i < N; i++) { tmp = arr[i]; for (j = i; j >= increment; j -= increment) { if (arr[j - increment] > tmp) arr[j] = arr[j - increment]; else break; } arr[j] = tmp; } } } /**************************************************************************/ /* 簡單選擇排序(simple selection sort) 就是通過n-i次關鍵字之間的比較,從n-i+1 * 個記錄中選擇關鍵字最小的記錄,並和第i(1<=i<=n)個記錄交換之 * 儘管與氣泡排序同為O(n^2),但簡單選擇排序的效能要略優於氣泡排序 */ void SelectSort(int arr[], int num) { int i, j, Mindex; for (i = 0; i < num; i++) { Mindex = i; for (j = i + 1; j < num; j++) { if (arr[j] < arr[Mindex]) Mindex = j; } swap1(&arr[i], &arr[Mindex]); } } /********************************************************************************/ /*假設初始序列含有n個記錄,則可以看成n個有序的子序列,每個子序列的長度為1,然後 * 兩兩歸併,得到(不小於n/2的最小整數)個長度為2或1的有序子序列,再兩兩歸併,... * 如此重複,直至得到一個長度為n的有序序列為止,這種排序方法稱為2路歸併排序 * 時間複雜度為O(nlogn),空間複雜度為O(n+logn),如果非遞迴實現歸併,則避免了遞迴時深度為logn的棧空間 * 空間複雜度為O(n) */ /*lpos is the start of left half, rpos is the start of right half*/ void merge(int a[], int tmp_array[], int lpos, int rpos, int rightn) { int i, leftn, num_elements, tmpos; leftn = rpos - 1; tmpos = lpos; num_elements = rightn - lpos + 1; /*main loop*/ while (lpos <= leftn && rpos <= rightn) if (a[lpos] <= a[rpos]) tmp_array[tmpos++] = a[lpos++]; else tmp_array[tmpos++] = a[rpos++]; while (lpos <= leftn) /*copy rest of the first part*/ tmp_array[tmpos++] = a[lpos++]; while (rpos <= rightn) /*copy rest of the second part*/ tmp_array[tmpos++] = a[rpos++]; /*copy array back*/ for (i = 0; i < num_elements; i++, rightn--) a[rightn] = tmp_array[rightn]; } void msort(int a[], int tmp_array[], int left, int right) { int center; if (left < right) { center = (right + left) / 2; msort(a, tmp_array, left, center); msort(a, tmp_array, center + 1, right); merge(a, tmp_array, left, center + 1, right); } } void merge_sort(int a[], int n) { int *tmp_array; tmp_array = (int *)malloc(n * sizeof(int)); if (tmp_array != NULL) { msort(a, tmp_array, 0, n - 1); free(tmp_array); } else printf("No space for tmp array!\n"); } /************************************************************************************/ /* 堆是具有下列性質的完全二叉樹:每個節點的值都大於或等於其左右孩子節點的值,稱為大頂堆; * 或者每個節點的值都小於或等於其左右孩子節點的值,稱為小頂堆*/ /*堆排序就是利用堆進行排序的方法.基本思想是:將待排序的序列構造成一個大頂堆.此時,整個序列的最大值就是堆頂 * 的根結點.將它移走(其實就是將其與堆陣列的末尾元素交換, 此時末尾元素就是最大值),然後將剩餘的n-1個序列重新 * 構造成一個堆,這樣就會得到n個元素的次大值.如此反覆執行,便能得到一個有序序列了 */ /* 時間複雜度為 O(nlogn),好於冒泡,簡單選擇,直接插入的O(n^2) */ // 構造大頂堆 #define leftChild(i) (2*(i) + 1) void percDown(int *arr, int i, int N) { int tmp, child; for (tmp = arr[i]; leftChild(i) < N; i = child) { child = leftChild(i); if (child != N - 1 && arr[child + 1] > arr[child]) child++; if (arr[child] > tmp) arr[i] = arr[child]; else break; } arr[i] = tmp; } void HeapSort(int *arr, int N) { int i; for (i = N / 2; i >= 0; i--) percDown(arr, i, N); for (i = N - 1; i > 0; i--) { swap1(&arr[0], &arr[i]); percDown(arr, 0, i); } } int main(void) { int arr[] = { 9, 2, 5, 8, 3, 4, 7, 1, 6, 10}; HeapSort(arr, 10); for (int i = 0; i < 10; i++) cout << arr[i] << ' '; cout << endl; return 0; } |
注:上述7種都是比較排序,下面3種都是非比較排序,理論上可以達到O(n),比比較排序要快,但是這3種都是有其應用背景才能發揮作用的,否則適得其反。
八:計數排序
計數排序(Counting sort)是一種穩定的排序演算法。計數排序使用一個額外的陣列C,其中第i個元素是待排序陣列A中值等於i的元素的個數。然後根據陣列C來將A中的元素排到正確的位置。
演算法的步驟如下:
- 找出待排序的陣列中最大和最小的元素
- 統計陣列中每個值為i的元素出現的次數,存入陣列C的第i項
- 對所有的計數累加(從C中的位置為1的元素開始,每一項和前一項相加)
- 反向填充目標陣列:將每個元素i放在新陣列的第C(i)項,每放一個元素就將C(i)減去1
九:桶排序
桶排序 (Bucket sort)或所謂的箱排序,是一個排序演算法,工作的原理是將陣列分到有限數量的桶子裡。每個桶子再個別排序(有可能再使用別的排序演算法或是以遞迴方式繼續使用桶排序進行排序)
桶排序以下列程式進行:
- 設定一個定量的陣列當作空桶子。
- 尋訪序列,並且把專案一個一個放到對應的桶子去。(hash)
- 對每個不是空的桶子進行排序。
- 從不是空的桶子裡把專案再放回原來的序列中。
十:基數排序
基數排序(英語:Radix
sort)是一種非比較型整數排序演算法,其原理是將整數按位數切割成不同的數字,然後按每個位數分別比較。由於整數也可以表達字串(比如名字或日期)和特定格式的浮點數,所以基數排序也不是隻能使用於整數。
它是這樣實現的:將所有待比較數值(正整數)統一為同樣的數位長度,數位較短的數前面補零。然後,從最低位開始,依次進行一次排序。這樣從最低位排序一直到最高位排序完成以後, 數列就變成一個有序序列。
基數排序的方式可以採用LSD(Least significant digital)或MSD(Most significant digital),LSD的排序方式由鍵值的最右邊開始,而MSD則相反,由鍵值的最左邊開始。
|
1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 |
#include<stdio.h>
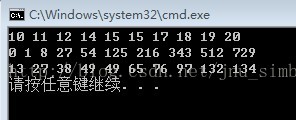
#include<string.h> #include<algorithm> using namespace std; /*****************計數排序*******************************/ void CountSort(int *arr, int num) { int mindata = arr[0]; int maxdata = arr[0]; for (int i = 1; i < num; i++) { if (arr[i] > maxdata) maxdata = arr[i]; if (arr[i] < mindata) mindata = arr[i]; } int size = maxdata - mindata + 1; //申請空間並初始化為0 int *pCount = (int *)malloc(sizeof(int) * size); memset(pCount, 0, sizeof(int)*size); //記錄排序計數,每出現一次在對應位置加1 for (int i = 0; i < num; i++) ++pCount[arr[i]-mindata]; //確定不比該位置大的資料個數 for (int i = 1; i < size; i++) pCount[i] += pCount[i - 1]; //加上前一個的計數 int *pSort = (int *)malloc(sizeof(int) * num); memset((char*)pSort, 0, sizeof(int) * num); //從末尾開始拷貝是為了重複資料首先出現的排在前面,即穩定排序 for (int i = num - 1; i >= 0; i--) { //包含自己需要減1,重複資料迴圈回來也需要減1 --pCount[arr[i]-mindata]; pSort[pCount[arr[i]-mindata]] = arr[i]; } //拷貝到原陣列 for (int i = 0; i < num; i++) arr[i] = pSort[i]; free(pCount); free(pSort); } /*****************桶排序*****************************/ struct Node { int key_; struct Node *next_; Node(int key) { key_ = key; next_ = NULL; } }; #define bucket_size 10 //與陣列元素個數相等 void buck_sort(int arr[], int num) { Node *bucket_table[bucket_size]; memset(bucket_table, 0, sizeof(bucket_table)); //建立每一個頭節點,頭節點的key儲存當前桶的資料量 for (int i = 0; i < bucket_size; i++) bucket_table[i] = new Node(0); int maxValue = arr[0]; for (int i = 1; i < num; i++) { if (arr[i] > maxValue) maxValue = arr[i]; } for (int j = 0; j < num; j++) { Node *ptr = new Node(arr[j]);//其餘節點的key儲存資料 //對映函式計算桶號 // index = (value * number_of_elements) / (maxvalue + 1) int index = (arr[j] * bucket_size) / (maxValue + 1); Node *head = bucket_table[index]; //該桶還沒有資料 if (head->key_ == 0) { bucket_table[index]->next_ = ptr; (bucket_table[index]->key_)++; } else { //找到合適的位置插入 while (head->next_ != NULL && head->next_->key_ <= ptr->key_) head = head->next_; ptr->next_ = head->next_; head->next_ = ptr; (bucket_table[index]->key_)++; } } //將桶中的資料拷貝回原陣列 int m, n; for (m = 0, n = 0; n < num && m < bucket_size; m++, n++) { Node *ptr = bucket_table[m]->next_; while (ptr != NULL) { arr[n] = ptr->key_; ptr = ptr->next_; n++; } n--; } //釋放分配的動態空間 for (m = 0; m < bucket_size; m++) { Node *ptr = bucket_table[m]; Node *tmp = NULL; while (ptr != NULL) { tmp = ptr->next_; delete ptr; ptr = tmp; } } } /****************************************************/ /******************** 基數排序LSD*********************/ void base_sort_ISD(int *arr, int num) { Node *buck[10]; // 建立一個連結串列陣列 Node *tail[10]; //儲存每條連結串列尾節點指標集合, //這樣插入buck陣列時就不用每次遍歷到末尾 int i, MaxValue, kth, high, low; Node *ptr; for(MaxValue = arr[0], i = 1; i < num; i++) MaxValue = max(MaxValue, arr[i]); memset(buck, 0, sizeof(buck)); memset(tail, 0, sizeof(buck)); for(low = 1; high = low * 10, low < MaxValue; low *= 10) { //只要沒排好序就一直排序 for(i = 0; i < num; i++) { //往桶裡放 kth = (arr[i] % high) / low;//取出資料的某一位,作為桶的索引 ptr = new Node(arr[i]); //建立新節點 //接到末尾 if (buck[kth] != NULL) { tail[kth]->next_ = ptr; tail[kth] = ptr; } else { buck[kth] = ptr; tail[kth] = ptr; } } //把桶中的資料放回陣列中(同條連結串列是從頭到尾) for (kth = 0, i = 0; kth < num; i++) { while (buck[i] != NULL) { arr[kth++] = buck[i]->key_; ptr = buck[i]; buck[i] = buck[i]->next_; delete ptr; } } memset(tail, 0, sizeof(buck)); } } /**************************************************************/ int main(void) { int arr1[] = {10, 15, 11, 20, 15, 18, 19, 12, 14, 17}; int size1 = sizeof(arr1) / sizeof(arr1[0]); CountSort(arr1, size1); for (int i = 0; i < size1; i++) printf("%d ", arr1[i]); printf("\n"); int arr2[] = {54, 8, 216, 512, 27, 729, 0, 1, 343, 125}; int size2 = sizeof(arr2) / sizeof(arr2[0]); base_sort_ISD(arr2, size2); for (int i = 0; i < size2; i++) printf("%d ", arr2[i]); printf("\n"); int arr3[] = {49, 38, 65, 97, 76, 13, 27, 49, 132, 134}; int size3 = sizeof(arr3) / sizeof(arr3[0]); buck_sort(arr3, size3); for (int i = 0; i < size3; i++) printf("%d ", arr3[i]); printf("\n"); return 0; } |
輸出為:
相關文章
- 排序演算法Python(冒泡、選擇、快速、插入、希爾、歸併排序)排序演算法Python
- (建議收藏)2020最新排序演算法總結:冒泡、選擇、插入、希爾、快速、歸併、堆排序、基數排序排序演算法
- 七、排序,選擇、冒泡、希爾、歸併、快速排序實現排序
- 排序演算法之冒泡,選擇,插入和希爾排序演算法
- Python八大演算法的實現,插入排序、希爾排序、氣泡排序、快速排序、直接選擇排序、堆排序、歸併排序、基數排序。Python演算法排序
- 排序演算法之歸併,快速,堆和桶排序演算法
- 插入、冒泡、歸併、堆排序、快排總結排序
- PHP排序演算法(插入,選擇,交換,冒泡,快速)PHP排序演算法
- 排序(2)--選擇排序,歸併排序和基數排序排序
- 常見的三種排序演算法(選擇,冒泡,計數)排序演算法
- 幾大排序總結(上)!圖解解析+程式碼例項(冒泡、選擇、插入、希爾、快排)排序圖解
- 桶排序 選擇,插入排序排序
- 排序演算法(氣泡排序,選擇排序,插入排序,希爾排序)排序演算法
- 單連結串列的排序(插入,選擇,冒泡)排序
- 排序演算法集:冒泡、插入、希爾、快速(陣列實現、連結串列實現)排序演算法陣列
- 最簡單易懂的三種排序演算法:冒泡、選擇、插入排序演算法
- 基礎排序(冒泡、選擇、插入)學習筆記排序筆記
- 計數排序、桶排序和基數排序排序
- 【資料結構與演算法】非比較排序(計數排序、桶排序、基數排序)資料結構演算法排序
- 排序演算法 - 快速插入排序和希爾排序排序演算法
- 關於js陣列的六種演算法---水桶排序,氣泡排序,選擇排序,快速排序,插入排序,希爾排序的理解。JS陣列演算法排序
- 歸併排序和基數排序排序
- 計數排序vs基數排序vs桶排序排序
- 基於桶的排序之基數排序以及排序方法總結排序
- 排序法:選擇、冒泡、插入和快排排序
- Python演算法之---冒泡,選擇,插入排序演算法Python演算法排序
- 單連結串列的冒泡,快排,選擇,插入,歸併等多圖詳解
- 【Java資料結構與演算法】第八章 快速排序、歸併排序和基數排序Java資料結構演算法排序
- php插入排序,快速排序,歸併排序,堆排序PHP排序
- (戀上資料結構筆記):計數排序、基數排序 、桶排序資料結構筆記排序
- 排序演算法總結之歸併排序排序演算法
- 基於桶的排序之計數排序排序
- 桶排序和基數排序排序
- 排序演算法總結之希爾排序排序演算法
- PHP 常見4種排序 氣泡排序、選擇排序、插入排序、快速排序PHP排序
- 【資料結構與演算法】內部排序之五:計數排序、基數排序和桶排序(含完整原始碼)資料結構演算法排序原始碼
- 演算法導論學習之三:排序之C語言實現:選擇排序,插入排序,歸併排序演算法排序C語言
- 前端也能學演算法:JS版常見排序演算法-冒泡,插入,快排,歸併前端演算法JS排序