HDU 4940 Destroy Transportation system(圖論)
這道題目當時做的時候想的是,如果找到一個點他的d值之和大於 d+b值之和,就可以。竟然就這麼過了啊。不過題解上還有一種做法,好像有點難。以後在補一補那種做法吧。
Destroy Transportation system
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others)Total Submission(s): 289 Accepted Submission(s): 181
Problem Description
Tom is a commander, his task is destroying his enemy’s transportation system.
Let’s represent his enemy’s transportation system as a simple directed graph G with n nodes and m edges. Each node is a city and each directed edge is a directed road. Each edge from node u to node v is associated with two values D and B, D is the cost to destroy/remove such edge, B is the cost to build an undirected edge between u and v.
His enemy can deliver supplies from city u to city v if and only if there is a directed path from u to v. At first they can deliver supplies from any city to any other cities. So the graph is a strongly-connected graph.
He will choose a non-empty proper subset of cities, let’s denote this set as S. Let’s denote the complement set of S as T. He will command his soldiers to destroy all the edges (u, v) that u belongs to set S and v belongs to set T.
To destroy an edge, he must pay the related cost D. The total cost he will pay is X. You can use this formula to calculate X:
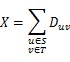
After that, all the edges from S to T are destroyed. In order to deliver huge number of supplies from S to T, his enemy will change all the remained directed edges (u, v) that u belongs to set T and v belongs to set S into undirected edges. (Surely, those edges exist because the original graph is strongly-connected)
To change an edge, they must remove the original directed edge at first, whose cost is D, then they have to build a new undirected edge, whose cost is B. The total cost they will pay is Y. You can use this formula to calculate Y:
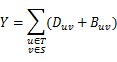
At last, if Y>=X, Tom will achieve his goal. But Tom is so lazy that he is unwilling to take a cup of time to choose a set S to make Y>=X, he hope to choose set S randomly! So he asks you if there is a set S, such that Y<X. If such set exists, he will feel unhappy, because he must choose set S carefully, otherwise he will become very happy.
Let’s represent his enemy’s transportation system as a simple directed graph G with n nodes and m edges. Each node is a city and each directed edge is a directed road. Each edge from node u to node v is associated with two values D and B, D is the cost to destroy/remove such edge, B is the cost to build an undirected edge between u and v.
His enemy can deliver supplies from city u to city v if and only if there is a directed path from u to v. At first they can deliver supplies from any city to any other cities. So the graph is a strongly-connected graph.
He will choose a non-empty proper subset of cities, let’s denote this set as S. Let’s denote the complement set of S as T. He will command his soldiers to destroy all the edges (u, v) that u belongs to set S and v belongs to set T.
To destroy an edge, he must pay the related cost D. The total cost he will pay is X. You can use this formula to calculate X:
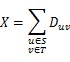
After that, all the edges from S to T are destroyed. In order to deliver huge number of supplies from S to T, his enemy will change all the remained directed edges (u, v) that u belongs to set T and v belongs to set S into undirected edges. (Surely, those edges exist because the original graph is strongly-connected)
To change an edge, they must remove the original directed edge at first, whose cost is D, then they have to build a new undirected edge, whose cost is B. The total cost they will pay is Y. You can use this formula to calculate Y:
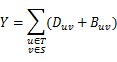
At last, if Y>=X, Tom will achieve his goal. But Tom is so lazy that he is unwilling to take a cup of time to choose a set S to make Y>=X, he hope to choose set S randomly! So he asks you if there is a set S, such that Y<X. If such set exists, he will feel unhappy, because he must choose set S carefully, otherwise he will become very happy.
Input
There are multiply test cases.
The first line contains an integer T(T<=200), indicates the number of cases.
For each test case, the first line has two numbers n and m.
Next m lines describe each edge. Each line has four numbers u, v, D, B.
(2=<n<=200, 2=<m<=5000, 1=<u, v<=n, 0=<D, B<=100000)
The meaning of all characters are described above. It is guaranteed that the input graph is strongly-connected.
The first line contains an integer T(T<=200), indicates the number of cases.
For each test case, the first line has two numbers n and m.
Next m lines describe each edge. Each line has four numbers u, v, D, B.
(2=<n<=200, 2=<m<=5000, 1=<u, v<=n, 0=<D, B<=100000)
The meaning of all characters are described above. It is guaranteed that the input graph is strongly-connected.
Output
For each case, output "Case #X: " first, X is the case number starting from 1.If such set doesn’t exist, print “happy”, else print “unhappy”.
Sample Input
2
3 3
1 2 2 2
2 3 2 2
3 1 2 2
3 3
1 2 10 2
2 3 2 2
3 1 2 2
Sample Output
Case #1: happy
Case #2: unhappy
Hint
In first sample, for any set S, X=2, Y=4.
In second sample. S= {1}, T= {2, 3}, X=10, Y=4.#include <algorithm>
#include <iostream>
#include <stdlib.h>
#include <string.h>
#include <iomanip>
#include <stdio.h>
#include <string>
#include <queue>
#include <cmath>
#include <stack>
#include <map>
#include <set>
#define eps 1e-10
///#define M 1000100
#define LL __int64
///#define LL long long
///#define INF 0x7ffffff
#define INF 0x3f3f3f3f
#define PI 3.1415926535898
#define zero(x) ((fabs(x)<eps)?0:x)
const int maxn = 2010;
using namespace std;
struct node
{
int x, y;
} f[maxn];
int main()
{
int T;
cin >>T;
int Case = 1;
while(T--)
{
int n, m;
cin >>n>>m;
int x, y;
int d, b;
for(int i = 0; i <= n; i++) f[i].x = f[i].y = 0;
for(int i = 0; i < m; i++)
{
scanf("%d %d %d %d",&x, &y, &d, &b);
f[x].y += d;
f[y].x += (d+b);
}
int flag = 0;
for(int i = 1; i <= n; i++)
{
if(f[i].x < f[i].y)
{
flag = 1;
break;
}
}
cout<<"Case #"<<Case++<<": ";
if(flag) cout<<"unhappy"<<endl;
else cout<<"happy"<<endl;
}
return 0;
}相關文章
- Hdu 1792 A New Change Problem 結論
- hdu 1792 A New Change Problem(數論)
- org.apache.coyote.AbstractProtocol.destroy Failed to destroy end point associated with ProtocolHandlApacheProtocolAI
- SAP MM Transportation of PR Release Strategy with Classification
- HDU 2254 奧運(數論+矩陣)矩陣
- 【博弈論】HDU - 7216 Triangle GameGAM
- 《The Google File System》論文研讀Go
- clipboard.destroy報錯
- POJ1797 Heavy Transportation【並查集+貪心】並查集
- AT_abc362_c [ABC362C] Transportation Expenses
- 圖論圖論
- Google檔案系統(Google File System)論文Go
- HDU 1060 Leftmost Digit(數論,c++)GitC++
- 數學規律題,數論知識:hdu1792
- hdu Yet another end of the world(擴充套件歐幾里得定理推論)套件
- 大資料理論篇HDFS的基石——Google File System大資料Go
- 【模板】圖論圖論
- 模板 - 圖論圖論
- 圖論板子圖論
- 【坑】Tkinter ‘NoneType‘ object has no attribute ‘destroy‘NoneObject
- 基礎圖論圖論
- 圖論(Graph Theory)圖論Graph Theory
- CQNK圖論 1圖論
- 【圖論】尤拉圖圖論
- 圖論題單圖論
- 圖論筆記圖論筆記
- 圖論總結圖論
- 片 - 圖論 - 1圖論
- 圖論連通性圖論
- 最短路圖論圖論
- 圖論基礎圖論
- 圖論-有向圖縮點圖論
- ¡Hola Euler! 圖資料庫的理論基礎:圖論資料庫圖論
- laravel中delete()方法和destroy()方法的區別Laraveldelete
- Terraform入門 – 4. destroy 基礎設施ORM
- 《The Design of a Practical System for Fault-Tolerant Virtual Machines》論文研讀Mac
- HDU5424Rikka with Graph II(哈密頓圖判斷)
- HDU 4279 2012網路賽Number(數論 尤拉函式結論約數個數)函式