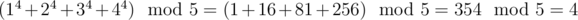codeforces 260 div2 A,B,C

畫船聽雨發表於2014-08-09

A:水題，結構體排序後，看兩個陣列的是否序列相同。

B：分別寫出來1，2，3，4，的n次方對5取餘。你會發現和對5取餘有一個迴圈節。如果%4 = 0，輸出4，否則輸出0.

寫一個大數取餘就過了。

B. Fedya and Maths
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output

Fedya studies in a gymnasium. Fedya's maths hometask is to calculate the following expression:

(1n + 2n + 3n + 4n) mod 5

for given value of n. Fedya managed to complete the task. Can you? Note that given number n can be extremely large (e.g. it can exceed any integer type of your programming language).

Input

The single line contains a single integer n (0 ≤ n ≤ 10105). The number doesn't contain any leading zeroes.

Output

Print the value of the expression without leading zeros.

Sample test(s)
input
4
output
4
input
124356983594583453458888889
output
0
Note

Operation x mod y means taking remainder after division x by y.

Note to the first sample:

#include <algorithm>
#include <iostream>
#include <stdlib.h>
#include <string.h>
#include <iomanip>
#include <stdio.h>
#include <string>
#include <queue>
#include <cmath>
#include <stack>
#include <ctime>
#include <map>
#include <set>
#define eps 1e-9
///#define M 1000100
///#define LL __int64
#define LL long long
///#define INF 0x7ffffff
#define INF 0x3f3f3f3f
#define PI 3.1415926535898
#define zero(x) ((fabs(x)<eps)?0:x)

using namespace std;

const int maxn = 1000010;

int main()
{
    string s;
    while(cin >>s)
    {
        int n= s.size();
        int cnt = s[0]-'0';
        for(int i = 1; i < n; i++)
        {
            cnt %= 4;
            cnt = (cnt*10+(s[i]-'0'))%4;
        }
        if(cnt%4 == 0)
            cout<<4<<endl;
        else cout<<0<<endl;
    }
}

C：給你一些數，你取了一個數那麼比這個數大1，和小1的數字就會被刪掉。問你最大能取到的數的和。

先根據數字進行雜湊，然後線性的dp一遍，dp[i][1] = ma(dp[i-2][0], dp[i-2][1]) + vis[i]*i,dp[i][0] = max(dp[i-1][0], dp[i-1][1]).1代表取這個數，0代表不取。注意資料型別要用long long。

C. Boredom
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output

Alex doesn't like boredom. That's why whenever he gets bored, he comes up with games. One long winter evening he came up with a game and decided to play it.

Given a sequence a consisting of n integers. The player can make several steps. In a single step he can choose an element of the sequence (let's denote it ak) and delete it, at that all elements equal to ak + 1 and ak - 1 also must be deleted from the sequence. That step brings ak points to the player.

Alex is a perfectionist, so he decided to get as many points as possible. Help him.

Input

The first line contains integer n (1 ≤ n ≤ 105) that shows how many numbers are in Alex's sequence.

The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 105).

Output

Print a single integer — the maximum number of points that Alex can earn.

Sample test(s)
input
2
1 2
output
2
input
3
1 2 3
output
4
input
9
1 2 1 3 2 2 2 2 3
output
10
Note

Consider the third test example. At first step we need to choose any element equal to 2. After that step our sequence looks like this [2, 2, 2, 2]. Then we do 4 steps, on each step we choose any element equals to 2. In total we earn 10 points.


#include <algorithm>
#include <iostream>
#include <stdlib.h>
#include <string.h>
#include <iomanip>
#include <stdio.h>
#include <string>
#include <queue>
#include <cmath>
#include <stack>
#include <ctime>
#include <map>
#include <set>
#define eps 1e-9
///#define M 1000100
///#define LL __int64
#define LL long long
///#define INF 0x7ffffff
#define INF 0x3f3f3f3f
#define PI 3.1415926535898
#define zero(x) ((fabs(x)<eps)?0:x)

using namespace std;

const int maxn = 1000010;

LL vis[maxn];
LL dp[maxn][2];

int main()
{
    int n;
    while(cin >>n)
    {
        int x;
        memset(vis, 0, sizeof(vis));
        memset(dp, 0, sizeof(dp));
        for(int i = 0; i < n; i++)
        {
            scanf("%d",&x);
            vis[x] ++;
        }
        dp[1][1] = vis[1];
        dp[2][1] = vis[2]*2;
        dp[2][0] = dp[1][1];
        for(int i = 3; i <= maxn-10; i++)
        {
            dp[i][1] = max(dp[i-2][0], dp[i-2][1])+vis[i]*i;
            dp[i][0] = max(dp[i-1][0], dp[i-1][1]);
        }
        cout<<max(dp[maxn-10][0], dp[maxn-10][1])<<endl;
    }
    return 0;
}


相關文章