HDU 4923 Room and Moor(瞎搞題)
瞎搞題啊。找出1 1 0 0這種序列,然後存起來,這種情況下最好的選擇是1的個數除以這段的總和。然後從前向後掃一遍,變掃邊進行合併。每次合併,合併的是他的前驅。這樣到最後從t-1找出的那條鏈就是最後滿足條件的數的大小。
Room and Moor
Time Limit: 12000/6000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)Total Submission(s): 307 Accepted Submission(s): 90
Problem Description
PM Room defines a sequence A = {A1, A2,..., AN}, each of which is either 0 or 1. In order to beat him, programmer Moor has to construct another sequence B = {B1, B2,... , BN} of the same length,
which satisfies that:
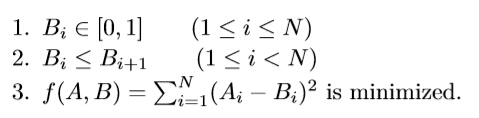
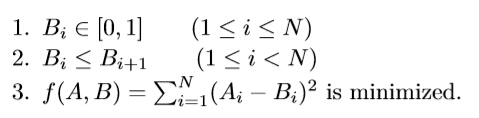
Input
The input consists of multiple test cases. The number of test cases T(T<=100) occurs in the first line of input.
For each test case:
The first line contains a single integer N (1<=N<=100000), which denotes the length of A and B.
The second line consists of N integers, where the ith denotes Ai.
For each test case:
The first line contains a single integer N (1<=N<=100000), which denotes the length of A and B.
The second line consists of N integers, where the ith denotes Ai.
Output
Output the minimal f (A, B) when B is optimal and round it to 6 decimals.
Sample Input
4
9
1 1 1 1 1 0 0 1 1
9
1 1 0 0 1 1 1 1 1
4
0 0 1 1
4
0 1 1 1
Sample Output
1.428571
1.000000
0.000000
0.000000
Source
#include <algorithm>
#include <iostream>
#include <stdlib.h>
#include <string.h>
#include <iomanip>
#include <stdio.h>
#include <string>
#include <queue>
#include <cmath>
#include <stack>
#include <ctime>
#include <map>
#include <set>
#define eps 1e-9
///#define M 1000100
#define LL __int64
///#define LL long long
///#define INF 0x7ffffff
#define INF 0x3f3f3f3f
#define PI 3.1415926535898
#define zero(x) ((fabs(x)<eps)?0:x)
using namespace std;
const int maxn = 1000010;
int num[maxn];
int sum[maxn][2];
int pre[maxn];
double x[maxn];
int main()
{
int T;
cin >>T;
while(T--)
{
int n;
scanf("%d",&n);
for(int i = 0; i < n; i++) scanf("%d",&num[i]);
int t = 0;
int cnt1 = 0;
int cnt2 = 0;
if(!num[0]) cnt1 = 1;
if(num[0]) cnt2 = 1;
for(int i = 1; i < n; i++)
{
if(num[i] > num[i-1])
{
sum[t][0] = cnt1;
sum[t++][1] = cnt2;
cnt1 = cnt2 = 0;
if(!num[i]) cnt1++;
if(num[i]) cnt2++;
continue;
}
if(!num[i]) cnt1++;
if(num[i]) cnt2++;
}
sum[t][0] = cnt1;
sum[t][1] = cnt2;
t++;
for(int i = 0 ; i < t; i++) x[i] = (1.0*sum[i][1]/((sum[i][0]+sum[i][1])*1.0));
pre[0] = -1;
for(int i = 1; i < t; i++)
{
if(x[i] < x[i-1])
{
sum[i][0] += sum[i-1][0];
sum[i][1] += sum[i-1][1];
x[i] = 1.0*sum[i][1]/(sum[i][1]+sum[i][0])*1.0;
pre[i] = pre[i-1];
int p = pre[i];
while(p != -1)
{
if(x[i] < x[p])
{
sum[i][0] += sum[p][0];
sum[i][1] += sum[p][1];
x[i] = 1.0*sum[i][1]/(sum[i][0]+sum[i][1])*1.0;
pre[i] = pre[p];
p = pre[p];
continue;
}
break;
}
continue;
}
pre[i] = i-1;
}
int p = pre[t-1];
double ans =0;
ans += sum[t-1][0]*pow(x[t-1], 2)+sum[t-1][1]*pow(x[t-1]-1, 2);
while(p != -1)
{
ans += sum[p][0]*pow(x[p], 2)+sum[p][1]*pow(x[p]-1, 2);
p = pre[p];
}
printf("%.6lf\n",ans);
}
return 0;
}
相關文章
- HDU 4923 Room and MoorOOM
- HDU 4925 Apple Tree (瞎搞)APP
- HDU 2478 Slides(瞎搞,預處理)IDE
- ZOJ First Digit(瞎搞)Git
- chat roomOOM
- Leetcode Meeting room問題系列 - 2LeetCodeOOM
- Leetcode Meeting room問題系列 - 1LeetCodeOOM
- HDU 不要62 題解
- [譯] Room ? CoroutinesOOM
- Leetcode 252. Meeting Room 253. Meeting Room IILeetCodeOOM
- 人生房間Life RoomOOM
- 簡單的揹包問題(入門)HDU2602 HDU2546 HDU1864
- hdu2045 遞迴水題遞迴
- hdu2048遞迴問題遞迴
- hdu2049遞迴問題遞迴
- 杭電ACM hdu 2110 Crisis of HDU 解題報告(母函式)ACM函式
- 杭電ACM hdu 1171 Big Event in HDU 解題報告(母函式)ACM函式
- Room Database完全使用手冊OOMDatabase
- Room ORM 資料庫框架OOMORM資料庫框架
- The room sexy Samantha Jones of Sex and the CityOOM
- hdu5365 簡單幾何問題
- Facebook面試題 meeting rooms 求同時最多meeting room的時間面試題OOM
- Leetcode 253: meeting roomLeetCodeOOM
- [譯]從 SQLite 逐步遷移到 RoomSQLiteOOM
- [譯] 從 SQLite 逐步遷移到 RoomSQLiteOOM
- HDU 5319 Painter (模擬 腦洞題)AI
- 關於Room資料庫,拼寫模糊查詢語句遇到的問題OOM資料庫
- HDU 1556 Color the ball 線段樹入門題
- hdu4400 STL應用 查詢思維題
- HDU4342 History repeat itself數學規律題
- hdu 3507 斜率優化DP入門題優化
- HDU 1241Oil Deposits(簡單搜尋題)
- HDU 4422 The Little Girl who Picks Mushrooms(簡單題)OOM
- Room & Kotlin 符號的處理OOMKotlin符號
- Android O 遷移測試:RoomAndroidOOM
- Android架構元件Room的使用Android架構元件OOM
- 使用Room持久庫儲存資料OOM
- 數學規律題,數論知識:hdu1792