HDU 1227 Fast Food(簡單二維dp)
題意是在n個餐廳之間選擇k個地方修建倉庫使得,各個餐廳到倉庫的距離和最小。
dp[i][j] = min{dp[i][j], dp[i-1][m]+w[m+1][j]}。i表示倉庫數目,j表示第幾個餐廳。狀態轉移方程式的意思是:到達j的時候區間(i,j)上所擁有的最小的值。到達j的時候可以選擇j位置上不修建倉庫dp[i][j] = dp[i][j]。或者選擇修倉庫那麼之前已經有i-1個倉庫修建好了,所以只能從i-1到j-1之間選擇修建第i個倉庫,所以從i-1->j-1列舉m。然後加上一個增量w[m+1][j]。表示加上i後這一段上增加的值的最小。
Fast Food
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submission(s): 1909 Accepted Submission(s): 815
Problem Description
The fastfood chain McBurger owns several restaurants along a highway. Recently, they have decided to build several depots along the highway, each one located at a restaurant and supplying several of the restaurants with the needed ingredients. Naturally, these
depots should be placed so that the average distance between a restaurant and its assigned depot is minimized. You are to write a program that computes the optimal positions and assignments of the depots.
To make this more precise, the management of McBurger has issued the following specification: You will be given the positions of n restaurants along the highway as n integers d1 < d2 < ... < dn (these are the distances measured from the company's headquarter, which happens to be at the same highway). Furthermore, a number k (k <= n) will be given, the number of depots to be built.
The k depots will be built at the locations of k different restaurants. Each restaurant will be assigned to the closest depot, from which it will then receive its supplies. To minimize shipping costs, the total distance sum, defined as
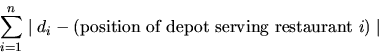
must be as small as possible.
Write a program that computes the positions of the k depots, such that the total distance sum is minimized.
To make this more precise, the management of McBurger has issued the following specification: You will be given the positions of n restaurants along the highway as n integers d1 < d2 < ... < dn (these are the distances measured from the company's headquarter, which happens to be at the same highway). Furthermore, a number k (k <= n) will be given, the number of depots to be built.
The k depots will be built at the locations of k different restaurants. Each restaurant will be assigned to the closest depot, from which it will then receive its supplies. To minimize shipping costs, the total distance sum, defined as
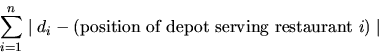
must be as small as possible.
Write a program that computes the positions of the k depots, such that the total distance sum is minimized.
Input
The input file contains several descriptions of fastfood chains. Each description starts with a line containing the two integers n and k. n and k will satisfy 1 <= n <= 200, 1 <= k <= 30, k <= n. Following this will n lines containing one integer each, giving
the positions di of the restaurants, ordered increasingly.
The input file will end with a case starting with n = k = 0. This case should not be processed.
The input file will end with a case starting with n = k = 0. This case should not be processed.
Output
For each chain, first output the number of the chain. Then output a line containing the total distance sum.
Output a blank line after each test case.
Output a blank line after each test case.
Sample Input
6 3
5
6
12
19
20
27
0 0
Sample Output
Chain 1
Total distance sum = 8
#include <algorithm>
#include <iostream>
#include <stdlib.h>
#include <string.h>
#include <iomanip>
#include <stdio.h>
#include <string>
#include <queue>
#include <cmath>
#include <stack>
#include <map>
#include <set>
#define eps 1e-7
#define M 10001000
//#define LL __int64
#define LL long long
#define INF 0x3f3f3f3f
#define PI 3.1415926535898
const int maxn = 101000;
using namespace std;
int dp[500][500];
int w[500][500];
int num[500];
int main()
{
int k, n;
int Case = 1;
while(cin >>n>>k)
{
if(!n && !k)
break;
memset(dp, INF, sizeof(dp));
memset(w, 0 , sizeof(w));
memset(num, 0, sizeof(num));
for(int i = 1; i <= n; i++)
cin >>num[i];
for(int i = 1; i <= n; i++)
for(int j = i; j <= n; j++)
for(int m = i; m <= j; m++)
w[i][j] += abs(num[m]-num[(i+j)/2]);
for(int i = 1; i <= n; i++)
dp[1][i] = w[1][i];
for(int i = 2; i <= k; i++)
for(int j = i; j <= n; j++)
for(int m = i-1; m <= j-1; m++)
dp[i][j] = min(dp[i][j], dp[i-1][m]+w[m+1][j]);
cout<<"Chain "<<Case++<<endl;
cout<<"Total distance sum = "<<dp[k][n]<<endl<<endl;
}
return 0;
}
相關文章
- HDU 5119 Happy Matt Friends(簡單二維dp)APP
- URAL 1577. E-mail(簡單二維dp)AI
- hdu 1069 Monkey and Banana(簡單dp)NaN
- hdu 3401 單調佇列+DP佇列
- HDU 1466 計算直線的交點數(簡單dp)
- hdu4374單調佇列+dp佇列
- PHP生成簡單二維碼PHP
- 二維碼簡單封裝封裝
- HDU 3530 Subsequence (dp+單調佇列)佇列
- HDU 2888 Check Corners(二維RMQ)MQ
- 簡單的Java二維碼應用Java
- HDU 3853 LOOPS(概率dp)OOP
- HDU 4669 Mutiples on a circle (DP , 統計)
- 用java做一個簡單的二維碼Java
- hdu 3665Seaside(簡單floyd)IDE
- HDU 4965 Fast Matrix Calculation(矩陣快速冪)AST矩陣
- 【基礎dp】HDU 1260 Tickets
- HDU 4455 Substrings(預處理+dp)
- phpqrcode生成動態二維碼簡單例項PHP單例
- hdu5365 簡單幾何問題
- c#簡單實現二維陣列和二維陣列列表List<>的轉置C#陣列
- Binary Tree Traversals(HDU1710)二叉樹的簡單應用二叉樹
- 簡單易用的二維碼掃描工具:QR Capture for MacAPTMac
- javascript實現二維陣列實現簡單介紹JavaScript陣列
- 使用 Swift 建立簡單的二維碼掃描應用Swift
- HDU 6415 Rikka with Nash Equilibrium (DP)UI
- HDU 3853 LOOPS:期望dp【網格型】OOP
- 【dp】HDU - 1069 Monkey and BananaNaN
- HDU 5119 Happy Matt Friends(DP)APP
- HDU 5326 Work (基礎樹形dp)
- hdu 4123 樹形DP+RMQMQ
- HDU 4770 Lights Against Dudely(列舉所有狀態 當然壯壓dp會很簡單)AI
- hdu 4287Intelligent IME(簡單hash)Intel
- hdu 1326 java (理解起來很簡單)Java
- URAL 1658. Sum of Digits(簡單dp)Git
- HDU3415 Max Sum of Max-K-sub-sequence (DP+單調佇列)佇列
- HDU 6274 Master of Sequence(思維+樹狀陣列+二分)AST陣列
- 自定義 React Native 二維碼掃描元件(簡單,易用!)React Native元件