異常點/離群點檢測演算法——LOF

wangyibo0201發表於2016-06-18
演算法

區域性異常因子演算法-Local Outlier Factor(LOF)

　　在資料探勘方面，經常需要在做特徵工程和模型訓練之前對資料進行清洗，剔除無效資料和異常資料。異常檢測也是資料探勘的一個方向，用於反作弊、偽基站、金融詐騙等領域。
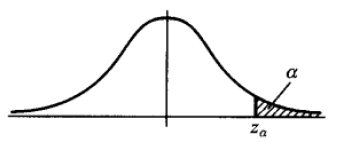
　　異常檢測方法，針對不同的資料形式，有不同的實現方法。常用的有基於分佈的方法，在上、下α分位點之外的值認為是異常值（例如圖1），對於屬性值常用此類方法。基於距離的方法，適用於二維或高維座標體系內異常點的判別，例如二維平面座標或經緯度空間座標下異常點識別，可用此類方法。
　　圖1
　　這次要介紹一下一種基於距離的異常檢測演算法，區域性異常因子LOF演算法（Local Outlier Factor）。
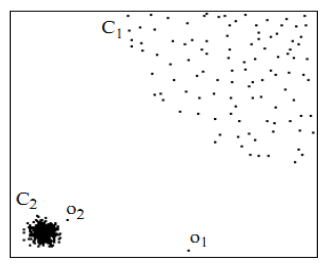
　　用視覺直觀的感受一下，如圖2，對於C1集合的點，整體間距，密度，分散情況較為均勻一致，可以認為是同一簇；對於C2集合的點，同樣可認為是一簇。o1、o2點相對孤立，可以認為是異常點或離散點。現在的問題是，如何實現演算法的通用性，可以滿足C1和C2這種密度分散情況迥異的集合的異常點識別。LOF可以實現我們的目標。
　　這裡寫圖片描述
　　下面介紹LOF演算法的相關定義：
　　1) d(p,o)

d(p, o)
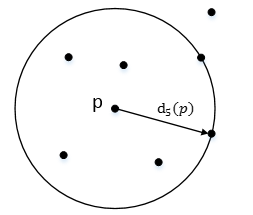
：兩點p和o之間的距離；
　　2) k-distance：第k距離
　　　　對於點p的第k距離dk(p)
d_{k}(p)
定義如下：
　　　　dk(p)=d(p,o)
d_{k}(p) = d(p, o)
，並且滿足：
　　　　　　a) 在集合中至少有不包括p在內的k
k
個點o,∈C{x≠p}
o^,\in C\{x \neq p\}
， 滿足d(p,o,)≤d(p,o)
d(p, o^,) \le d(p, o)
；
　　　　　　b) 在集合中最多有不包括p在內的k−1
k-1
個點o,∈C{x≠p}
o^,\in C\{x \neq p\}
，滿足d(p,o,)<d(p,o)
d(p, o^,) \lt d(p, o)
；
　　　　p的第k距離，也就是距離p第k遠的點的距離，不包括p，如圖3。
　　　　圖3
　　3) k-distance neighborhood of p：第k距離鄰域
　　　　點p的第k距離鄰域Nk(p)
N_k(p)
，就是p的第k距離即以內的所有點，包括第k距離。
　　　　因此p的第k鄰域點的個數 |Nk(p)|≥k
|N_k(p)| \ge k
。
　　4) reach-distance：可達距離
　　　　點o到點p的第k可達距離定義為：
　　　　reach−distancek(p,o)=max{k−distance(o),d(p,o)}
reach-distance_k(p, o) = max\{k-distance(o), d(p, o)\}

　　　　也就是，點o到點p的第k可達距離，至少是o的第k距離，或者為o、p間的真實距離。
　　　　這也意味著，離點o最近的k個點，o到它們的可達距離被認為相等，且都等於dk(o)
d_{k}(o)
。
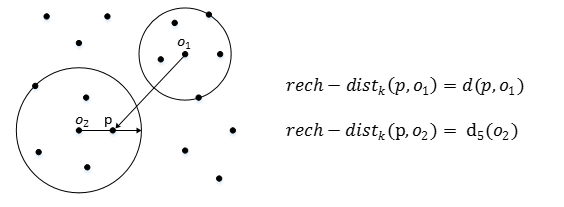
　　　　如圖4，o1
o_1
到p的第5可達距離為d(p,o1)
d(p,o_1)
，o2
o_2
到p的第5可達距離為d5(o2)
d_5(o_2)
。
　　　　這裡寫圖片描述
　　5) local reachability density：區域性可達密度
　　　　點ｐ的區域性可達密度表示為：

lrdk(p)=1/(∑o∈Nk(p)reach−distk(p,o)|Nk(p)|)
lrd_k(p) = 1 / (\frac{\sum_{o \in N_{k}(p)} reach-dist_k(p,o)}{|N_{k}(p)|})

　　　　表示點p的第k鄰域內點到p的平均可達距離的倒數。
　　　　注意，是p的鄰域點Nk(p)
N_k(p)
到p的可達距離，不是p到Nk(p)
N_k(p)
的可達距離，一定要弄清楚關係。並且，如果有重複點，那麼分母的可達距離之和有可能為0，則會導致lrd變為無限大，下面還會繼續提到這一點。
　　　　這個值的含義可以這樣理解，首先這代表一個密度，密度越高，我們認為越可能屬於同一簇，密度越低，越可能是離群點。如果p和周圍鄰域點是同一簇，那麼可達距離越可能為較小的dk(o)
d_{k}(o)
，導致可達距離之和較小，密度值較高；如果p和周圍鄰居點較遠，那麼可達距離可能都會取較大值d(p,o)
d(p, o)
，導致密度較小，越可能是離群點。
　　6) local outlier factor：區域性離群因子
　　　　點p的區域性離群因子表示為：
LOFk(p)=∑o∈Nk(p)lrdk(o)lrdk(p)|Nk(p)|=∑o∈Nk(p)lrdk(o)|Nk(p)|/lrdk(p)
LOF_k(p)=\frac{\sum_{o \in N_{k}(p)} \frac{lrd_k(o)}{lrd_k(p)}}{|N_k(p)|} = \frac{\sum_{o \in N_k(p)} lrd_k(o)}{|N_k(p)|} / lrd_k(p)

　　　　表示點p的鄰域點Nk(p)
N_k(p)
的區域性可達密度與點p的區域性可達密度之比的平均數。
　　　　如果這個比值越接近1，說明p的其鄰域點密度差不多，p可能和鄰域同屬一簇；如果這個比值越小於1，說明p的密度高於其鄰域點密度，p為密集點；如果這個比值越大於1，說明p的密度小於其鄰域點密度，p越可能是異常點。
　　現在概念定義已經介紹完了，現在再回過頭來看一下lof的思想，主要是通過比較每個點p和其鄰域點的密度來判斷該點是否為異常點，如果點p的密度越低，越可能被認定是異常點。至於密度，是通過點之間的距離來計算的，點之間距離越遠，密度越低，距離越近，密度越高，完全符合我們的理解。而且，因為lof對密度的是通過點的第k鄰域來計算，而不是全域性計算，因此得名為“區域性”異常因子，這樣，對於圖1的兩種資料集C1和C2，lof完全可以正確處理，而不會因為資料密度分散情況不同而錯誤的將正常點判定為異常點。
　　演算法思想已經講完了，現在進入乾貨環節，亮程式碼。
　　給一個python實現的lof演算法：
　　https://github.com/damjankuznar/pylof
　　再給一下我fork之後的程式碼：
　　https://github.com/wangyibo360/pylof
　　有區別：
　　上面提到了，對於重複點區域性可達密度可能會變為無限大的問題，我改的程式碼對這個問題做了處理，如果有重複點方面的場景，可以用我的程式碼，原始碼這塊有bug沒有fix，而且好像程式碼主人無蹤影了，提的pull也沒人管。。。

相關文章