淺談優化程式效能(下)

weixin_33912246發表於2012-05-13
優化

前言

在上一篇隨筆中，我們談到最小化一個計算中的運算元量不一定會提高它的效能。現在，就讓我們來解開為什麼會出現這種情況的原因吧。

處理器體系結構

在計算機的處理器中，處理一條指令包括很多操作，可以分為取指(fetch)、譯碼(decode)、執行(execute)、訪存(memory)、寫回(write back)和更新程式計數器(PC update)等幾個階段。這些階段可以在流水線上同時進行，如下圖所示：

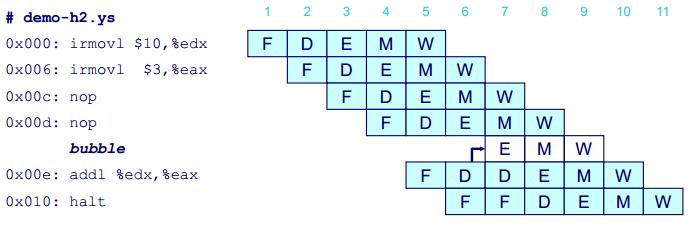
pipeline

上圖中，F、D、E、M 和 W 分別代表上述五個階段。當然，現代的處理器比這個示例要複雜得多，但是原理是一樣的。

  • 雙精度浮點數乘法: 延遲 5 發射時間 1
  • 雙精度浮點數加法: 延遲 3 發射時間 1
  • 單精度浮點數乘法: 延遲 4 發射時間 1
  • 單精度浮點數加法: 延遲 3 發射時間 1
  • 整數乘法：延遲 3 發射時間 1
  • 整數加法：延遲 1 發射時間 0.33

上面是 Intel Core i7 的一些算術運算的效能。這些時間對於其他處理器來說也是具有代表性的。每個運算都是由兩個週期計數值來刻畫的：

  1. 延遲(latency)，表示完成運算所需要的總時間。
  2. 發射時間(issue time)，表示兩個連續的同型別運算之間需要的最小時鐘週期數。

我們看到，大多數形式的算術運算的發射時間為 1，意思是說在每個時鐘週期，處理器都可以開始一條新的這樣的運算。這種很短的發射時間是通過使用流水線實現的。流水線化的功能單元實現為一系列的階段(stage)，每個階段完成一部分的運算。例如，一個典型的浮點加法器包含三個階段(所以有三個週期的延遲)：

  1. 處理指數值
  2. 將小數相加
  3. 對結果進行舍入

算術運算可以連續地通過各個階段，而不用等待一個操作完成後再開始下一個。只有當要執行的運算是連續的、邏輯上獨立的時候，才能利用這種功能。發射時間為 1 的功能單元被稱為完全流水線化的(fully pipelined)：每個時鐘週期都可以開始一個新的運算。整數加法的發射時間為 0.33，這是因為硬體有三個完全流水線化的能夠執行整數加法的功能單元。處理器有能力每個時鐘週期執行三個加法。

上述內容來源於《深入理解計算機系統(原書第2版)》。更詳細的內容請參閱該書，特別是“第四章 處理器體系結構”和“第五章 優化程式效能”。我們這篇文章討論的兩個演算法就來源於該書的“練習題 5.5”和“練習題 5.6”。

分析 poly 函式

下面就是 poly 函式的 C 語言源程式程式碼：

double poly(double a[], double x)
{
  double result = 0, p = 1;
  for (int i = 0; i < N; i++, p *= x) result += a[i] * p;
  return result;
}

我們在 openSuSE 12.1 作業系統中使用 objdump -d a.out 命令對上一篇隨筆中的測試程式進行反彙編，找出其中的 poly 函式的彙編程式碼如下所示：

0000000000400640 <poly>:
  400640:	66 0f 57 d2          	xorpd  %xmm2,%xmm2
  400644:	31 c0                	xor    %eax,%eax
  400646:	f2 0f 10 0d 92 01 00 	movsd  0x192(%rip),%xmm1        # 4007e0 <_IO_stdin_used+0x10>
  40064d:	00 
  40064e:	66 90                	xchg   %ax,%ax
  400650:	f2 0f 10 1c 07       	movsd  (%rdi,%rax,1),%xmm3
  400655:	48 83 c0 08          	add    $0x8,%rax
  400659:	48 3d a8 60 2f 0b    	cmp    $0xb2f60a8,%rax
  40065f:	f2 0f 59 d9          	mulsd  %xmm1,%xmm3
  400663:	f2 0f 59 c8          	mulsd  %xmm0,%xmm1
  400667:	f2 0f 58 d3          	addsd  %xmm3,%xmm2
  40066b:	75 e3                	jne    400650 <poly+0x10>
  40066d:	66 0f 28 c2          	movapd %xmm2,%xmm0
  400671:	c3                   	retq   
  400672:	66 66 66 66 66 2e 0f 	data32 data32 data32 data32 nopw %cs:0x0(%rax,%rax,1)
  400679:	1f 84 00 00 00 00 00

可以看出，poly 函式從地址 0x400640 處開始，這與上一篇隨筆中測試程式的執行結果相符。我們重點分析迴圈語句對應的從地址 0x400650 到 0x40066b 之間的程式碼：

# for (int i = 0; i < N; i++, p *= x) result += a[i] * p;
# i in %rax, a in %rdi, x in %xmm0, p in %xmm1, result in %xmm2, z in %xmm3
400650:	movsd  (%rdi,%rax,1),%xmm3  # z = a[i]
400655:	add    $0x8,%rax            # i++, for 8-byte pointer
400659:	cmp    $0xb2f60a8,%rax      # compare N : i
40065f:	mulsd  %xmm1,%xmm3          # z *= p
400663:	mulsd  %xmm0,%xmm1          # p *= x
400667:	addsd  %xmm3,%xmm2          # result += z
40066b:	jne    400650 <poly+0x10>   # if !=, goto loop

在 x86-64 體系結構中，%rax, %rdi 是 64-bit 的暫存器，%xmm0, %xmm1, %xmm2, %xmm3 是 128-bit 的浮點暫存器。

在本例中：

  • 整型迴圈變數 i 存放在 %rax 暫存器中。
  • 雙精度浮點型陣列 a 第一個元素的地址存放在 %rdi 暫存器中，注意這個地址是一個 64-bit 的指標，是整數值，而不是浮點值。
  • 雙精度浮點型輸入引數 x 存放在 %xmm0 暫存器中。
  • 中間變數 p 存放在 %xmm1 暫存器中。
  • 最終結果 result 存放在 %xmm2 暫存器中。
  • 此外，GCC C 編譯器還使用了一個臨時變數 z，存放在 %xmm3 暫存器中。

上述程式碼中的立即數的含義：

  • 0x08: 在 add 指令中使用，使 %rax 加上字長 8-byte，達到 i++ 的目的。
  • 0xb2f60a8: 在 cmp 指令中使用，它等於 187654312，除以字長 8-byte 就是 23456789，即 N 的值。
  • 0x400650: 在 jne 指令中使用，指明跳轉的目的地。

我們可以看到，這裡限制效能的計算是反覆地計算表示式 p *= x。這需要一個雙精度浮點數乘法(5個時鐘週期)，並且直到前一次迭代完成，下一次迭代的計算才能開始。兩次連續的迭代之間，還要計算表示式 z *= p， 這需要一個雙精度浮點乘法(5個時鐘週期)，以及計算表示式 result += z， 這需要一個雙精度浮點加法(3個時鐘週期)。這三個涉及浮點數運算的表示式的計算都可以在流水線上同時地進行。最終，完成一次迴圈迭代需要5個時鐘週期。

在這個彙編程式中，C 語言編譯器充分利用了處理器提供的指令級並行(instruction-level parallelism)能力，同時執行多條指令，以達到優化程式效能的目的。

分析 polyh 函式

這下面就是 polyh 函式的 C 語言源程式程式碼：

double polyh(double a[], double x)
{
  double result = 0;
  for (int i = N - 1; i >= 0; i--) result = result * x + a[i];
  return result;
}

對應的組合語言程式碼如下所示：

0000000000400680 <polyh>:
  400680:	66 0f 57 c9          	xorpd  %xmm1,%xmm1
  400684:	31 c0                	xor    %eax,%eax
  400686:	66 2e 0f 1f 84 00 00 	nopw   %cs:0x0(%rax,%rax,1)
  40068d:	00 00 00 
  400690:	f2 0f 59 c8          	mulsd  %xmm0,%xmm1
  400694:	f2 0f 58 8c 07 a0 60 	addsd  0xb2f60a0(%rdi,%rax,1),%xmm1
  40069b:	2f 0b 
  40069d:	48 83 e8 08          	sub    $0x8,%rax
  4006a1:	48 3d 58 9f d0 f4    	cmp    $0xfffffffff4d09f58,%rax
  4006a7:	75 e7                	jne    400690 <polyh+0x10>
  4006a9:	66 0f 28 c1          	movapd %xmm1,%xmm0
  4006ad:	c3                   	retq   
  4006ae:	66 90                	xchg   %ax,%ax

同樣可以看出，polyh 函式從地址 0x400680 處開始，也與上一篇隨筆中測試程式的執行結果相符。需要重點分析的迴圈語句位於地址 0x400690 到 0x4006a7 之間：

# for (int i = N - 1; i >= 0; i--) result = result * x + a[i];
# i in %rax, a in %rdi, x in %xmm0, result in %xmm1
400690:	mulsd  %xmm0,%xmm1                   # result *= x
400694:	addsd  0xb2f60a0(%rdi,%rax,1),%xmm1  # result += a[i]
40069d:	sub    $0x8,%rax                     # i--, for 8-byte pointer
4006a1:	cmp    $0xfffffffff4d09f58,%rax      # compare 0 : i
4006a7:	jne    400690 <polyh+0x10>           # if !=, goto loop

上述程式中幾個立即數的含義: 

  • 0x8: 在 sub 指令中使用，從 %rax 中減去字長 8-byte，達到 i-- 的目的。
  • 0xb2f60a0: 在 addsd 指令中使用，它等於 187654304，除以字長 8-byte 就是 23456788，即 N - 1 的值。
  • 0xfffffffff4d09f58: 在 cmp 指令中使用，它加上 0xb2f60a0 就是 0xfffffffffffffff8，再加上 0x8 就等於 0。
  • 0x400690: 在 jne 指令中使用，指明該指令跳轉的目的地。

類似地：

  • 整型迴圈變數 i 存放在 %rax 暫存器中。
  • 雙精度浮點型陣列 a 第一個元素的地址存放在 %rdi 暫存器中。
  • 雙精度浮點型輸入引數 x 存放在 %xmm0 暫存器中。
  • 最終結果 result 存放在 %xmm1 暫存器中。

我們可以看到，這裡限制效能的計算是求表示式 result *= x 和 result += a[i] 的值。從來自上一次迭代的 result 的值開始，我們必須先把它乘以 x (需要 5 個時鐘週期)，然後把它加上 a[i] (需要 3 個時鐘週期)，然後得到本次迭代的值。因此，完成一次迴圈迭代需要 8 個時鐘週期，比原始的演算法需要的 5 個時鐘週期更慢。注意，由於後一個表示式 result += a[i] 的計算需要前一個表示式 result *= x 的值，所以這兩個表示式的計算不能在流水線上同時進行。這裡由於資料相關(data dependency)，無法利用處理器提供的指令級並行能力來優化程式效能。

結論

優化程式效能不是一件簡單的事，必須對計算機系統的核心概念有所瞭解。現代計算機用複雜的技術來處理機器級程式，並行地執行許多指令，執行順序還可能不同於它們在程式中現出的順序。程式設計師必須理解這些處理器是如何工作的，從而調整他們的程式以獲得最大的速度。強烈推薦《深入理解計算機系統(原書第2版)》這本書。

參考資料

  1. 深入理解計算機系統(原書第2版)
  2. Wikipedia: Instruction-level paralelism
  3. Wikipedia: Data dependency

相關文章