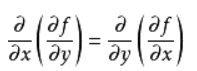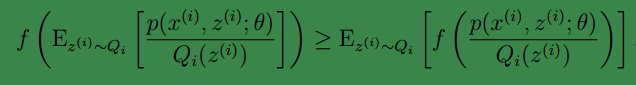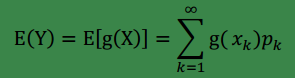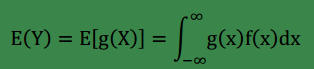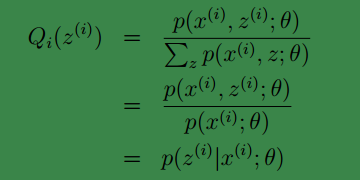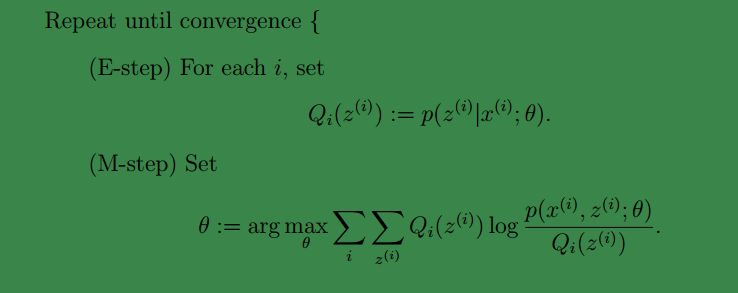（EM演算法）The EM Algorithm

之前介紹了EM演算法在混合高斯模型中的應用，現在讓我們來看看問什麼EM演算法可以用於這類問題。 
首先介紹一下Jensen 不等式

Jensen 不等式

我們知道，如果設 f 是定義域為實數的函式，如果對於所有的實數x，f′′(x)≥0，那麼 f 是凸函式。 
顯然我們的樣本x,是有很多屬性的，也就是說函式f的輸入是一個向量。這時f是凸函式就等價為為f的 hessian 矩陣 H 是半正定的（ H ≥ 0）。

begin-補充-hessian矩陣

對於一個實值多元函式f(x1,x2,...,xn) ，如果函式f 的二階偏導數都存在，則定義 f 的hessian矩陣為:

其中 D_i表示對第i 個變數的微分運算元，x⃗ =(x1,x2,...,xn),上式展開成矩陣形式如下： 

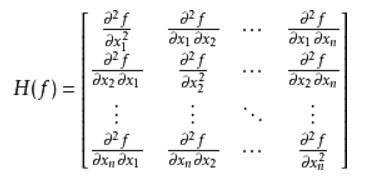
可見如果hessian矩陣存在那麼它必然是對稱的因為求偏導數時的求導順序並不影響最終結果： 

利用hessian進行多元函式極值的判定:

如果實值多元函式f(x1,x2,...,xn)二階連續可導，我們可以利用某個臨界點M處的hessian矩陣判斷該臨界點是否為極值： 
如果H(M)是正定矩陣，則臨界點M處是一個區域性的極小值。 
如果H(M)是負定矩陣，則臨界點M處是一個區域性的極大值。 
如果H(M)是不定矩陣，則臨界點M處不是極值。

end-補充-hessian矩陣

如果f′′(x)≥0,那麼它的hessian矩陣必然是半正定的，因為hessian矩陣中的每個元素都是有f的二階導數。 
下面給出jensen不等式定理： 
如果 f 是凸函式， X 是隨機變數，那麼 

特別地，如果 f 是嚴格凸函式，那麼E[f(X)]=f(EX)(以後都將f(E[X])表示成f(EX))當且僅當p(x=E[x])=1，即當且僅當X 是常量時。

為了便於理解我們們先看下面： 
凸函式的概念： 
【定義】如果函式f(x)滿足對定義域上任意兩個數x1,x2都有 f(x1+x22)≥f(x1)+f(x2)2，那麼f(x)為凸函式。 
注意哦開口向下的是凸,開口向上的是凹。 
如果不等式中等號只有 時才成立，我們分別稱它們為嚴格的凹凸函式. 
推廣下就是： 
對於任意的凹函式f(x)以及其定義域上n個數x1,x2,...,xn,那麼都有f(x1)+f(x2)+...+f(xn)n≥f(x1+x2+...+xnn) 
對於任意的凸函式f(x)以及其定義域上n個數x1,x2,...,xn,那麼都有f(x1)+f(x2)+...+f(xn)n≤f(x1+x2+...+xnn) 
如果上面凹凸是嚴格的，那麼不等式的等號只有x1=x2=...=xn才成立.

其實上面的結論就是我們的jensen不等式，相信大家都見過。 
可將jensen用圖形表示如下： 
 
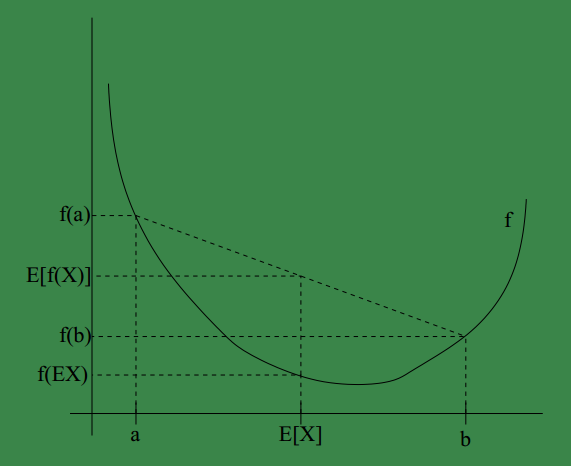
其中E(X)就是a+b2,E[f(X)]就是f(a)+f(b)2,顯然，在凸函式中E[f(X)]≥f(E[X])。

另外， f 是（嚴格）凹函式當且僅當−f 是（嚴格）凸函式。 
Jensen 不等式應用於凹函式時，不等號方向反向，也就是E[f(X)]≤f(E[X]).

EM演算法

假如我們有訓練樣本集{x(1),x(2),...,x(n)},我們之前求模型p(x,y)的引數的方式是利用似然值： 
 
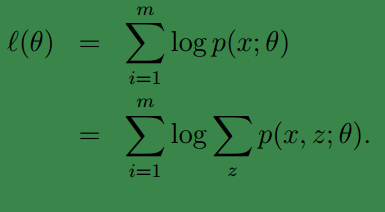
但是在上一篇中我們提到由於z(i)的值是不確定的隨機變數，因此不能通過求最大似然值的方式獲得引數。但是一般確定了 z 後，求解就容易了。

EM 是一種解決存在隱含變數優化問題的有效方法。其思想是：不斷地建立ℓ的下界（E 步），然後優化下界（ M 步）。這就話沒看懂吧！看不懂正常，下面來詳細介紹EM演算法： 
對於每一個樣例 i，讓Qi 表示該樣例隱含變數 z 的某種分佈， Qi 滿足的條件∑zQi(z)=1,Qi(z)≥0(如果 z 是連續性的，那麼Qi是概率密度函式，需要將求和符號換做積分符號)。 
這樣我們可以得到： 
 
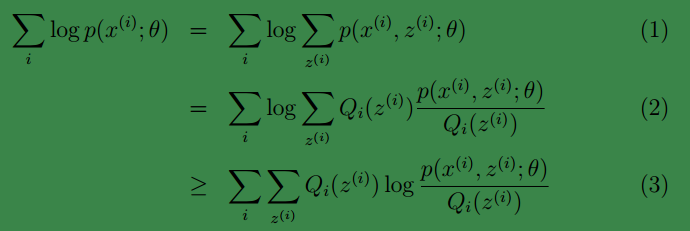
注： 
1、（1）到（2）比較直接，就是分子分母同乘以一個相等的函式。 
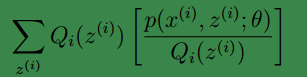
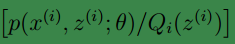
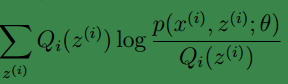
2、（2）到（3）利用了 Jensen不等式；首先log函式是凹函式。其次根據lazy Statistician規則，可知其實就是的數學期望，可以看作jensen不等式中的E[f(X)],同理可以看作jensen不等式中的f(E[X])；此時根據jensen不等式我們可得： 

begin-補充-Lazy Statistician規則

設 Y 是隨機變數X 的函式， Y=g(X)（ g 是連續函式），那麼 
（1） X 是離散型隨機變數，它的分佈律為P(X=xk)=pk，k=1,2,…。若∑∞k=1g(xk)pk絕對收斂，則有 

（2） X是連續型隨機變數，它的概率密度為f(x)，若∫∞−∞g(x)f(x)dx絕對收斂，則有 

end-補充

因此，對於任何一種分佈Qi，上面的式子(3)都給ℓ(θ)的值確定了一個下限。但是對於Qi的選擇，有多種可能，那種更好的？ 
（我們知道，在EM演算法中的E步中，我們的θ是已知的，即在當前條件下可獲得的θ）假設θ已經給定，那麼ℓ(θ)的值就決定於Qi(z(i))和p(x(i),z(i))了。我們可以通過調整這兩個概率使下界儘可能大（即使得(3)的值儘可能大）， 以逼近ℓ(θ)的真實值,顯然當(3)等於(2)時ℓ(θ)的下限最大。根據jensen不等式我們知道當且僅當X是常量時等號成立。這裡p(x(i),z(i);θ)Qi(z(i))就是jensen不等式中的X，我們假設p(x(i),z(i);θ)Qi(z(i))=c⟺p(x(i),z(i);θ)=cQi(z(i))⟺Qi(z(i))=p(x(i),z(i);θ)c 
其中c是一個不依賴於z^{(i)}的常數。我們知道∑zQi(z(i))=1，因此可得∑zp(x(i),z(i);θ)=∑zcQi(z(i))=c. 
進而可得： 
Qi(z(i))=p(x(i),z(i);θ)c=p(x(i),z(i);θ)∑zp(x(i),z(i);θ)=p(x(i),z(i);θ)p(x(i);θ) 
再利用條件概率公式可得:Qi(z(i))=p(z(i)|x(i);θ)

上面的推導有點亂，現在把他們壓縮下就是： 

現在我們知道Qi(z(i))該如何選擇啦，Qi(z(i))的計算公式就是後驗概率p(z(i)|x(i);θ). 
這一步就是E 步，建立ℓ(θ)的下界。接下來的M步，就是在給定Qi(z(i))後，調整θ，去極大化ℓ(θ)的下界（在固定Qi(z(i))後，下界還可以調整的更大）。 一般的EM演算法的步驟如下： 

下面讓我們來證明EM演算法的收斂性： 
假定θ(t)和θ(t+1)是 EM 第 t 次和 t+1 次迭代後的結果。 如果我們證明了ℓ(θ(t)) ≤ ℓ(θ(t+1))，也就是說極大似然估計單調增加，那麼最終我們會到達最大似然估計的最大值。 下面來證明，選定θ(t)後，我們得到 E 步，為了能取等號，選取Qi(z(i))如下： 
 
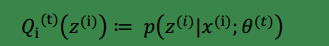
進而等號滿足： 
 
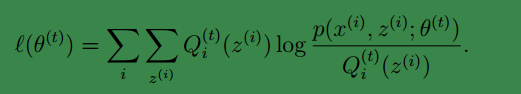
然後我們通過最大化上面等式的式右面獲得了新的引數θt+1. 
此時必然有： 
 
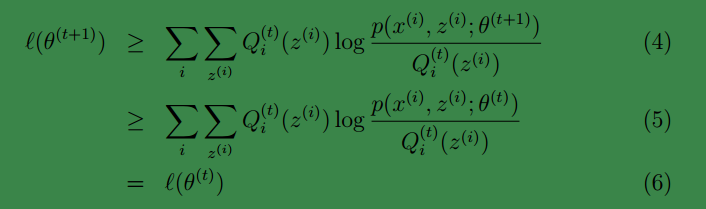
上面第一行是由式（3）得到，即基於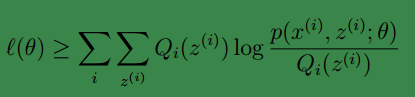 
第（ 5）步利用了 M 步的定義。第（ 5）步利用了 M 步的定義， M 步就是將θ(t)調整到θ(t+1)，即θ(t+1)的選擇是基於： 
因此（ 5）成立，（ 6）是之前的等式結果。 
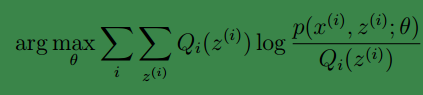
這樣就證明了ℓ(θ)會單調增加。因此EM演算法是收斂的。 
如果我們定義： 
 
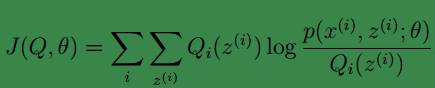
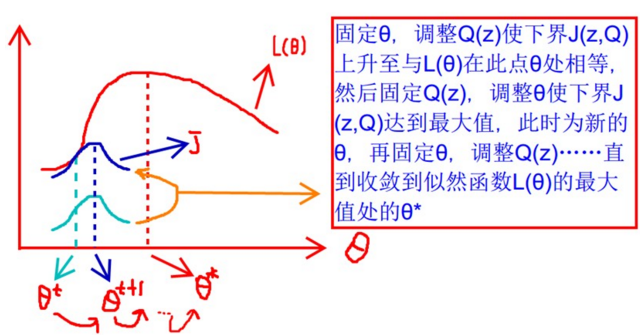
從前面的推導中我們知道ℓ(θ) ≥ J(Q, θ)， EM 可以看作是 J 的座標上升法， E 步固定θ，優化Q， M 步固定Q優化θ。 
下面從別人那偷了張圖，很好的說明了EM演算法的優化過程：