主成分分析（Principal components analysis）-最大方差解釋

在這一篇之前的內容是《Factor Analysis》，由於非常理論，打算學完整個課程後再寫。在寫這篇之前，我閱讀了PCA、SVD和LDA。這幾個模型相近，卻都有自己的特點。本篇打算先介紹PCA，至於他們之間的關係，只能是邊學邊體會了。PCA以前也叫做Principal factor analysis。

1. 問題

     真實的訓練資料總是存在各種各樣的問題：

1、 比如拿到一個汽車的樣本，裡面既有以“千米/每小時”度量的最大速度特徵，也有“英里/小時”的最大速度特徵，顯然這兩個特徵有一個多餘。

2、 拿到一個數學系的本科生期末考試成績單，裡面有三列，一列是對數學的興趣程度，一列是複習時間，還有一列是考試成績。我們知道要學好數學，需要有濃厚的興趣，所以第二項與第一項強相關，第三項和第二項也是強相關。那是不是可以合併第一項和第二項呢？

3、 拿到一個樣本，特徵非常多，而樣例特別少，這樣用迴歸去直接擬合非常困難，容易過度擬合。比如北京的房價：假設房子的特徵是（大小、位置、朝向、是否學區房、建造年代、是否二手、層數、所在層數），搞了這麼多特徵，結果只有不到十個房子的樣例。要擬合房子特徵->房價的這麼多特徵，就會造成過度擬合。

4、 這個與第二個有點類似，假設在IR中我們建立的文件-詞項矩陣中，有兩個詞項為“learn”和“study”，在傳統的向量空間模型中，認為兩者獨立。然而從語義的角度來講，兩者是相似的，而且兩者出現頻率也類似，是不是可以合成為一個特徵呢？

5、 在訊號傳輸過程中，由於通道不是理想的，通道另一端收到的訊號會有噪音擾動，那麼怎麼濾去這些噪音呢？

     回顧我們之前介紹的《模型選擇和規則化》，裡面談到的特徵選擇的問題。但在那篇中要剔除的特徵主要是和類標籤無關的特徵。比如“學生的名字”就和他的“成績”無關，使用的是互資訊的方法。

     而這裡的特徵很多是和類標籤有關的，但裡面存在噪聲或者冗餘。在這種情況下，需要一種特徵降維的方法來減少特徵數，減少噪音和冗餘，減少過度擬合的可能性。

     下面探討一種稱作主成分分析（PCA）的方法來解決部分上述問題。PCA的思想是將n維特徵對映到k維上（k<n），這k維是全新的正交特徵。這k維特徵稱為主元，是重新構造出來的k維特徵，而不是簡單地從n維特徵中去除其餘n-k維特徵。

2. PCA計算過程

     首先介紹PCA的計算過程：

     假設我們得到的2維資料如下：

     

     行代表了樣例，列代表特徵，這裡有10個樣例，每個樣例兩個特徵。可以這樣認為，有10篇文件，x是10篇文件中“learn”出現的TF-IDF，y是10篇文件中“study”出現的TF-IDF。也可以認為有10輛汽車，x是千米/小時的速度，y是英里/小時的速度，等等。

     第一步分別求x和y的平均值，然後對於所有的樣例，都減去對應的均值。這裡x的均值是1.81，y的均值是1.91，那麼一個樣例減去均值後即為（0.69,0.49），得到

     

     第二步，求特徵協方差矩陣，如果資料是3維，那麼協方差矩陣是

     

     這裡只有x和y，求解得

     

     對角線上分別是x和y的方差，非對角線上是協方差。協方差大於0表示x和y若有一個增，另一個也增；小於0表示一個增，一個減；協方差為0時，兩者獨立。協方差絕對值越大，兩者對彼此的影響越大，反之越小。

     第三步，求協方差的特徵值和特徵向量，得到

     

     上面是兩個特徵值，下面是對應的特徵向量，特徵值0.0490833989對應特徵向量為，這裡的特徵向量都歸一化為單位向量。

    第四步，將特徵值按照從大到小的順序排序，選擇其中最大的k個，然後將其對應的k個特徵向量分別作為列向量組成特徵向量矩陣。

     這裡特徵值只有兩個，我們選擇其中最大的那個，這裡是1.28402771，對應的特徵向量是。

     第五步，將樣本點投影到選取的特徵向量上。假設樣例數為m，特徵數為n，減去均值後的樣本矩陣為DataAdjust(m*n)，協方差矩陣是n*n，選取的k個特徵向量組成的矩陣為EigenVectors(n*k)。那麼投影后的資料FinalData為

     

     這裡是

     FinalData(10*1) = DataAdjust(10*2矩陣)×特徵向量

     得到結果是

     

     這樣，就將原始樣例的n維特徵變成了k維，這k維就是原始特徵在k維上的投影。

     上面的資料可以認為是learn和study特徵融合為一個新的特徵叫做LS特徵，該特徵基本上代表了這兩個特徵。

     上述過程有個圖描述：

     

     正號表示預處理後的樣本點，斜著的兩條線就分別是正交的特徵向量（由於協方差矩陣是對稱的，因此其特徵向量正交），最後一步的矩陣乘法就是將原始樣本點分別往特徵向量對應的軸上做投影。

     如果取的k=2，那麼結果是

     

     這就是經過PCA處理後的樣本資料，水平軸（上面舉例為LS特徵）基本上可以代表全部樣本點。整個過程看起來就像將座標系做了旋轉，當然二維可以圖形化表示，高維就不行了。上面的如果k=1，那麼只會留下這裡的水平軸，軸上是所有點在該軸的投影。

     這樣PCA的過程基本結束。在第一步減均值之後，其實應該還有一步對特徵做方差歸一化。比如一個特徵是汽車速度（0到100），一個是汽車的座位數（2到6），顯然第二個的方差比第一個小。因此，如果樣本特徵中存在這種情況，那麼在第一步之後，求每個特徵的標準差，然後對每個樣例在該特徵下的資料除以。

     歸納一下，使用我們之前熟悉的表示方法，在求協方差之前的步驟是：

     

     其中是樣例，共m個，每個樣例n個特徵，也就是說是n維向量。是第i個樣例的第j個特徵。是樣例均值。是第j個特徵的標準差。

     整個PCA過程貌似及其簡單，就是求協方差的特徵值和特徵向量，然後做資料轉換。但是有沒有覺得很神奇，為什麼求協方差的特徵向量就是最理想的k維向量？其背後隱藏的意義是什麼？整個PCA的意義是什麼？

3. PCA理論基礎

     要解釋為什麼協方差矩陣的特徵向量就是k維理想特徵，我看到的有三個理論：分別是最大方差理論、最小錯誤理論和座標軸相關度理論。這裡簡單探討前兩種，最後一種在討論PCA意義時簡單概述。

3.1 最大方差理論

     在訊號處理中認為訊號具有較大的方差，噪聲有較小的方差，訊雜比就是訊號與噪聲的方差比，越大越好。如前面的圖，樣本在橫軸上的投影方差較大，在縱軸上的投影方差較小，那麼認為縱軸上的投影是由噪聲引起的。

因此我們認為，最好的k維特徵是將n維樣本點轉換為k維後，每一維上的樣本方差都很大。

     比如下圖有5個樣本點：（已經做過預處理，均值為0，特徵方差歸一）

     

     下面將樣本投影到某一維上，這裡用一條過原點的直線表示（前處理的過程實質是將原點移到樣本點的中心點）。

     

     假設我們選擇兩條不同的直線做投影，那麼左右兩條中哪個好呢？根據我們之前的方差最大化理論，左邊的好，因為投影后的樣本點之間方差最大。

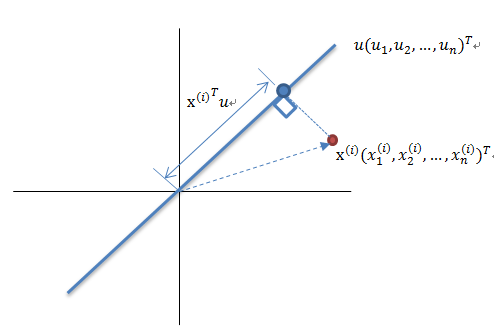
     這裡先解釋一下投影的概念：

     

     紅色點表示樣例，藍色點表示在u上的投影，u是直線的斜率也是直線的方向向量，而且是單位向量。藍色點是在u上的投影點，離原點的距離是（即或者）由於這些樣本點（樣例）的每一維特徵均值都為0，因此投影到u上的樣本點（只有一個到原點的距離值）的均值仍然是0。

     回到上面左右圖中的左圖，我們要求的是最佳的u，使得投影后的樣本點方差最大。

     由於投影后均值為0，因此方差為：

     

     中間那部分很熟悉啊，不就是樣本特徵的協方差矩陣麼（的均值為0，一般協方差矩陣都除以m-1，這裡用m）。

     用來表示，表示，那麼上式寫作

      

     由於u是單位向量，即，上式兩邊都左乘u得，

     即

     We got it！就是的特徵值，u是特徵向量。最佳的投影直線是特徵值最大時對應的特徵向量，其次是第二大對應的特徵向量，依次類推。

     因此，我們只需要對協方差矩陣進行特徵值分解，得到的前k大特徵值對應的特徵向量就是最佳的k維新特徵，而且這k維新特徵是正交的。得到前k個u以後，樣例通過以下變換可以得到新的樣本。

     

     其中的第j維就是在上的投影。

     通過選取最大的k個u，使得方差較小的特徵（如噪聲）被丟棄。

     這是其中一種對PCA的解釋，第二種是錯誤最小化，放在下一篇介紹。