支援向量機(五)SMO演算法
11 SMO優化演算法(Sequential minimal optimization)
SMO演算法由Microsoft Research的John C. Platt在1998年提出,併成為最快的二次規劃優化演算法,特別針對線性SVM和資料稀疏時效能更優。關於SMO最好的資料就是他本人寫的《Sequential Minimal Optimization A Fast Algorithm for Training Support Vector Machines》了。
我拜讀了一下,下面先說講義上對此方法的總結。
首先回到我們前面一直懸而未解的問題,對偶函式最後的優化問題:
要解決的是在引數![]() 上求最大值W的問題,至於
上求最大值W的問題,至於![]() 和
和![]() 都是已知數。C由我們預先設定,也是已知數。
都是已知數。C由我們預先設定,也是已知數。
按照座標上升的思路,我們首先固定除![]() 以外的所有引數,然後在
以外的所有引數,然後在![]() 上求極值。等一下,這個思路有問題,因為如果固定
上求極值。等一下,這個思路有問題,因為如果固定![]() 以外的所有引數,那麼
以外的所有引數,那麼![]() 將不再是變數(可以由其他值推出),因為問題中規定了
將不再是變數(可以由其他值推出),因為問題中規定了
因此,我們需要一次選取兩個引數做優化,比如![]() 和
和![]() ,此時
,此時![]() 可以由
可以由![]() 和其他參數列示出來。這樣迴帶到W中,W就只是關於
和其他參數列示出來。這樣迴帶到W中,W就只是關於![]() 的函式了,可解。
的函式了,可解。
這樣,SMO的主要步驟如下:
意思是,第一步選取一對![]() 和
和![]() ,選取方法使用啟發式方法(後面講)。第二步,固定除
,選取方法使用啟發式方法(後面講)。第二步,固定除![]() 和
和![]() 之外的其他引數,確定W極值條件下的
之外的其他引數,確定W極值條件下的![]() ,
,![]() 由
由![]() 表示。
表示。
SMO之所以高效就是因為在固定其他引數後,對一個引數優化過程很高效。
下面討論具體方法:
假設我們選取了初始值![]() 滿足了問題中的約束條件。接下來,我們固定
滿足了問題中的約束條件。接下來,我們固定![]() ,這樣W就是
,這樣W就是![]() 和
和![]() 的函式。並且
的函式。並且![]() 和
和![]() 滿足條件:
滿足條件:
由於![]() 都是已知固定值,因此為了方面,可將等式右邊標記成實數值
都是已知固定值,因此為了方面,可將等式右邊標記成實數值![]() 。
。
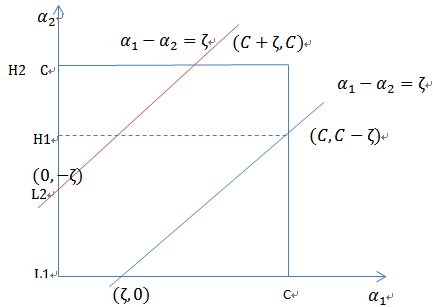
當![]() 和
和![]() 異號時,也就是一個為1,一個為-1時,他們可以表示成一條直線,斜率為1。如下圖:
異號時,也就是一個為1,一個為-1時,他們可以表示成一條直線,斜率為1。如下圖:
然後反代入W中,得
展開後W可以表示成![]() 。其中a,b,c是固定值。這樣,通過對W進行求導可以得到
。其中a,b,c是固定值。這樣,通過對W進行求導可以得到![]() ,然而要保證
,然而要保證![]() 滿足
滿足![]() ,我們使用
,我們使用![]() 表示求導求出來的
表示求導求出來的![]() ,然而最後的
,然而最後的![]() ,要根據下面情況得到:
,要根據下面情況得到:
下面進入Platt的文章,來找到啟發式搜尋的方法和求b值的公式。
這邊文章使用的符號表示有點不太一樣,不過實質是一樣的,先來熟悉一下文章中符號的表示。
文章中定義特徵到結果的輸出函式為
原始的優化問題為:
求導得到:
經過對偶後為:
這裡與W函式是一樣的,只是符號求反後,變成求最小值了。![]() 和
和![]() 是一樣的,都表示第i個樣本的輸出結果(1或-1)。
是一樣的,都表示第i個樣本的輸出結果(1或-1)。
由公式(7)代入(1)中可知,
這個過程和之前對偶過程一樣。
重新整理我們要求的問題為:
與之對應的KKT條件為:
這個KKT條件說明,在兩條間隔線外面的點,對應前面的係數![]() 為0,在兩條間隔線裡面的對應
為0,在兩條間隔線裡面的對應![]() 為C,在兩條間隔線上的對應的係數
為C,在兩條間隔線上的對應的係數![]() 在0和C之間。
在0和C之間。
將我們之前得到L和H重新拿過來:
之前我們將問題進行到這裡,然後說將![]() 用
用![]() 表示後代入W中,這裡將代入
表示後代入W中,這裡將代入![]() 中,得
中,得
其中
這裡的![]() 和
和![]() 代表某次迭代前的原始值,因此是常數,而
代表某次迭代前的原始值,因此是常數,而![]() 和
和![]() 是變數,待求。公式(24)中的最後一項是常數。
是變數,待求。公式(24)中的最後一項是常數。
其中
代入(24)中,得
如果![]() 的二階導數大於0(凹函式),那麼一階導數為0時,就是極小值了。
的二階導數大於0(凹函式),那麼一階導數為0時,就是極小值了。
假設其二階導數為0(一般成立),那麼上式化簡為:
將w和v代入後,繼續化簡推導,得(推導了六七行推出來了)
通常情況下目標函式是正定的,也就是說,能夠在直線約束方向上求得最小值,並且![]() 。
。
那麼
在特殊情況下,![]() 可能不為正,如果核函式K不滿足Mercer定理,那麼目標函式可能變得非正定,
可能不為正,如果核函式K不滿足Mercer定理,那麼目標函式可能變得非正定,![]() 可能出現負值。即使K是有效的核函式,如果訓練樣本中出現相同的特徵x,那麼
可能出現負值。即使K是有效的核函式,如果訓練樣本中出現相同的特徵x,那麼![]() 仍有可能為0。SMO演算法在
仍有可能為0。SMO演算法在![]() 不為正值的情況下仍有效。為保證有效性,我們可以推匯出
不為正值的情況下仍有效。為保證有效性,我們可以推匯出![]() 就是
就是![]() 的二階導數,
的二階導數,![]() ,
,![]() 沒有極小值,最小值在邊緣處取到(類比
沒有極小值,最小值在邊緣處取到(類比![]() ),
),![]() 時更是單調函式了,最小值也在邊緣處取得,而
時更是單調函式了,最小值也在邊緣處取得,而![]() 的邊緣就是L和H。這樣將
的邊緣就是L和H。這樣將![]() 和
和![]() 分別代入
分別代入![]() 中即可求得
中即可求得![]() 的最小值,相應的
的最小值,相應的![]() 還是
還是![]() 也可以知道了。具體計算公式如下:
也可以知道了。具體計算公式如下:
至此,迭代關係式出了b的推導式以外,都已經推出。
b每一步都要更新,因為前面的KKT條件指出了![]() 和
和![]() 的關係,而
的關係,而![]() 和b有關,在每一步計算出
和b有關,在每一步計算出![]() 後,根據KKT條件來調整b。
後,根據KKT條件來調整b。
b的更新有幾種情況:
來自羅林開的ppt
這樣全部引數的更新公式都已經介紹完畢,附加一點,如果使用的是線性核函式,我們就可以繼續使用w了,這樣不用掃描整個樣本庫來作內積了。
w值的更新方法為:
根據前面的
公式推匯出。
12 SMO中拉格朗日乘子的啟發式選擇方法
終於到了最後一個問題了,所謂的啟發式選擇方法主要思想是每次選擇拉格朗日乘子的時候,優先選擇樣本前面係數![]() 的
的![]() 作優化(論文中稱為無界樣例),因為在界上(
作優化(論文中稱為無界樣例),因為在界上(![]() 為0或C)的樣例對應的係數
為0或C)的樣例對應的係數![]() 一般不會更改。
一般不會更改。
這條啟發式搜尋方法是選擇第一個拉格朗日乘子用的,比如前面的![]() 。那麼這樣選擇的話,是否最後會收斂。可幸的是Osuna定理告訴我們只要選擇出來的兩個
。那麼這樣選擇的話,是否最後會收斂。可幸的是Osuna定理告訴我們只要選擇出來的兩個![]() 中有一個違背了KKT條件,那麼目標函式在一步迭代後值會減小。違背KKT條件不代表
中有一個違背了KKT條件,那麼目標函式在一步迭代後值會減小。違背KKT條件不代表![]() ,在界上也有可能會違背。是的,因此在給定初始值
,在界上也有可能會違背。是的,因此在給定初始值![]() =0後,先對所有樣例進行迴圈,迴圈中碰到違背KKT條件的(不管界上還是界內)都進行迭代更新。等這輪過後,如果沒有收斂,第二輪就只針對
=0後,先對所有樣例進行迴圈,迴圈中碰到違背KKT條件的(不管界上還是界內)都進行迭代更新。等這輪過後,如果沒有收斂,第二輪就只針對![]() 的樣例進行迭代更新。
的樣例進行迭代更新。
在第一個乘子選擇後,第二個乘子也使用啟發式方法選擇,第二個乘子的迭代步長大致正比於![]() ,選擇第二個乘子能夠最大化
,選擇第二個乘子能夠最大化![]() 。即當
。即當![]() 為正時選擇負的絕對值最大的
為正時選擇負的絕對值最大的![]() ,反之,選擇正值最大的
,反之,選擇正值最大的![]() 。
。
最後的收斂條件是在界內(![]() )的樣例都能夠遵循KKT條件,且其對應的
)的樣例都能夠遵循KKT條件,且其對應的![]() 只在極小的範圍內變動。
只在極小的範圍內變動。
至於如何寫具體的程式,請參考John C. Platt在論文中給出的虛擬碼。
13 總結
這份SVM的講義重點概括了SVM的基本概念和基本推導,中規中矩卻又讓人醍醐灌頂。起初讓我最頭疼的是拉格朗日對偶和SMO,後來逐漸明白拉格朗日對偶的重要作用是將w的計算提前並消除w,使得優化函式變為拉格朗日乘子的單一引數優化問題。而SMO裡面迭代公式的推導也著實讓我花費了不少時間。
對比這麼複雜的推導過程,SVM的思想確實那麼簡單。它不再像logistic迴歸一樣企圖去擬合樣本點(中間加了一層sigmoid函式變換),而是就在樣本中去找分隔線,為了評判哪條分界線更好,引入了幾何間隔最大化的目標。
之後所有的推導都是去解決目標函式的最優化上了。在解決最優化的過程中,發現了w可以由特徵向量內積來表示,進而發現了核函式,僅需要調整核函式就可以將特徵進行低維到高維的變換,在低維上進行計算,實質結果表現在高維上。由於並不是所有的樣本都可分,為了保證SVM的通用性,進行了軟間隔的處理,導致的結果就是將優化問題變得更加複雜,然而驚奇的是鬆弛變數沒有出現在最後的目標函式中。最後的優化求解問題,也被拉格朗日對偶和SMO演算法化解,使SVM趨向於完美。
另外,其他很多議題如SVM背後的學習理論、引數選擇問題、二值分類到多值分類等等還沒有涉及到,以後有時間再學吧。其實樸素貝葉斯在分類二值分類問題時,如果使用對數比,那麼也算作線性分類器。
相關文章
- 支援向量機|SMO演算法實現演算法
- 支援向量機原理(四)SMO演算法原理演算法
- 《Machine Learning in Action》—— 剖析支援向量機,優化SMOMac優化
- 《機器學習_07_01_svm_硬間隔支援向量機與SMO》機器學習
- 支援向量機原理(五)線性支援迴歸
- 分類演算法-支援向量機 SVM演算法
- 支援向量機原理(一) 線性支援向量機
- 支援向量機
- SVM 支援向量機演算法-原理篇演算法
- SVM 支援向量機演算法-實戰篇演算法
- 演算法金 | 再見,支援向量機 SVM!演算法
- 理解支援向量機
- 機器學習:支援向量機(SVM)機器學習
- 機器學習——支援向量機(SVM)機器學習
- 機器學習演算法筆記之5:支援向量機SVM機器學習演算法筆記
- scikit-learn 支援向量機演算法庫使用小結演算法
- [譯] 支援向量機(SVM)教程
- 機器學習——支援向量機SVM(一)機器學習
- 【機器學習】支援向量機分類機器學習
- svm的smo演算法演算法
- 支援向量機原理(三)線性不可分支援向量機與核函式函式
- 支援向量機原理(二) 線性支援向量機的軟間隔最大化模型模型
- 支援向量機(三)核函式函式
- 【機器學習】支援向量機(個人筆記)機器學習筆記
- 監督學習之支援向量機
- 機器學習之支援向量機的超平面機器學習
- 人工智慧-機器學習-支援向量機SVM人工智慧機器學習
- 機器學習實戰6(SMO演算法)機器學習演算法
- 吳恩達機器學習系列17:支援向量機吳恩達機器學習
- 機器學習基礎專題:支援向量機SVM機器學習
- 基於支援向量機的文字分類文字分類
- 機器學習之支援向量機原理和sklearn實踐機器學習
- 非線性支援向量機 與核函式函式
- 支援向量機(SVM)和python實現(二)Python
- 吳恩達機器學習筆記 —— 13 支援向量機吳恩達機器學習筆記
- 支援向量機python實現(簡易版)Python
- 支援向量機(Support Vector Machine,SVM)—— 線性SVMMac
- OpenCV筆記(3)實現支援向量機(SVM)OpenCV筆記
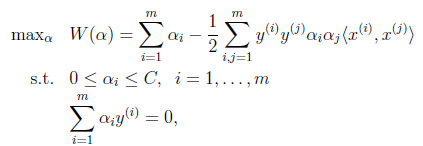
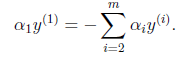

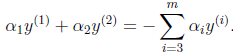
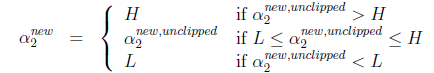

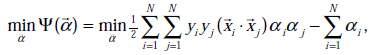
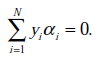
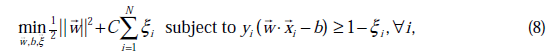

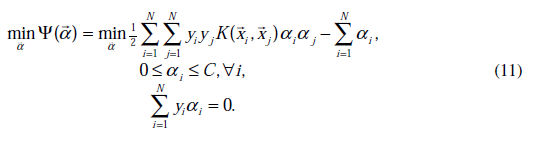

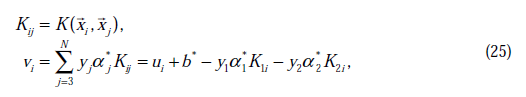
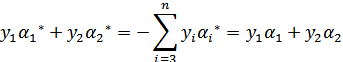
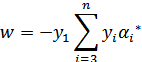
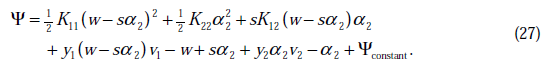
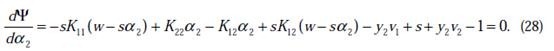
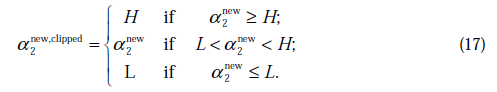
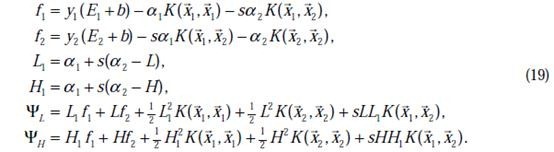

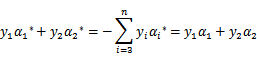
![clip_image068[1] clip_image068[1]](http://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103182044356550.png)