hihocoder 1232 || 2015北京網路賽F題 樹連剖分

life4711發表於2015-09-21

http://hihocoder.com/problemset/problem/1232

描述

"Couple Trees" are two trees, a husband tree and a wife tree. They are named because they look like a couple leaning on each other. They share a same root, and their branches are intertwined. In China, many lovers go to the couple trees. Under the trees, lovers wish to be accompanied by a lifetime.

Ada and her boyfriend Asa came to the couple trees as well. They were very interested in the trees. They were all ACMers, so after careful observation, they found out that these two trees could be considered as two "trees" in graph theory. These two trees shared N vertices which were labeled 1 to N, and they all had exactly N vertices. Vertices 1 was the root of both trees.

Ada and Asa wanted to know more about the trees' rough bark, so each of them put one thumb at a vertices. Then they moved their thumbs towards the root. Ada moved along the wife tree, and Asa moved along the husband tree. Of course, they could moved at different speed.

At that moment, a thought suddenly came to Ada's mind: their thumbs may meet before the root. Which one was the earliest possible meeting vertex? And how many vertices would Ada and Asa encounter on the way to the meeting vertex?

輸入

The input consists of no more than 8 test cases.

For each test case:

The first line contains two integers, N and M, indicating the number of vertices and the number of queries.(1≤N,M≤100,000)

The next line contains N−1 integers. It describes the structure of wife tree in this way: If the ith integer is k, it means that the vertex labeled k is the father vertex of the vertex labeled (i+1) . It's guaranteed that a vertex X's father vertex can't have a larger label than X does.

The next line describes the husband tree in the same way.

Then next M lines describe the queries. Each line contains two integers Xi and Yi. Let Ki be the earliest possible meeting vertex of the ith query (K0 is defined as 0). In the ith query, Ada's thumb was put at the vertex labeled (Xi+Ki−1) mod N + 1 and Asa's thumb was put at the vertex labeled (Yi+Ki−1) mod N + 1.(1≤Xi,Yi≤N) at the beginning.

輸出

For each test case:

Output the answer for each query in a single line. The answer contains three integers: the earliest possible meeting vertex, the number of the vertices Ada will encounter and the number of the vertices Asa will encounter (including the starting vertex and the ending vertex). In particular, if they put their thumb at the same vertex at first, the earliest possible meeting vertex should be the starting vertex.

提示

In the first test case:

The wife tree is like this:


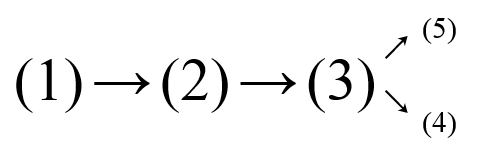
The husband tree is like this:


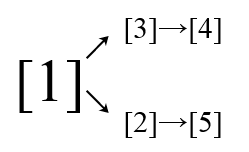
The query is (5)[4], and they may meet at {1,3}, so the earliest one is 3.

In the second test case:

The wife tree is like this:


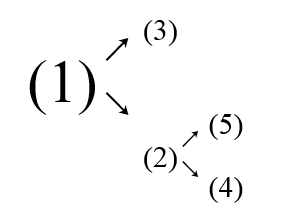
The husband tree is like this:


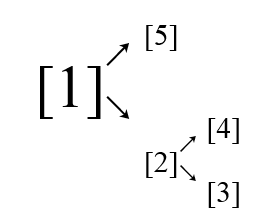
The first query is (1)[4], the second query is (2)[1], and the last one is (5)[2].

For the first query, they may only meet at 1.

For the second query, they may only meet at 1.

For the third query, they may meet at {1,2}, the earliest one is 2.

樣例輸入 
5 1
1 2 3 3
1 1 3 2
4 3
5 3
1 1 2 2
1 2 2 1
5 3
5 4
3 5
5 3
1 1 2 2
1 2 3 1
1 4
1 1
3 4
樣例輸出 
3 2 2
1 1 3
1 2 1
2 2 1
1 2 2
3 1 1
2 1 2
/**
hihocoder 1232 || 2015北京網路賽F題    樹連剖分
題目大意：有一對夫妻樹，他們的節點個數都一樣，都以1為根節點，並且兩個樹中所有的父親節點的編號都比其子孫節點小。
          現在分別給出兩個樹的結構，下面有m組詢問，妻子在妻子樹的x點出發，丈夫在丈夫樹的y點出發，只要二者所到節點的
          編號一樣就算相遇，二者只能望父親節點走，問每次二者的最早的相遇節點是什麼，並且求出二者經過的節點的個數
解題思路：樹連剖分後，每次在鏈上找匹配。每棵樹都剖一次，solve裡面兩個迴圈，列舉兩棵樹叢節點到根的鏈。
          首先題目裡面有個性質父節點的編號小於子節點，然後就是列舉看兩個鏈L1, L2是否有重複的點。對於每個點i, 找到i
          分別在兩棵樹中所在鏈的根f1, f2把i存在 f1, f2中，理論上來說應該用F[f1][f2].push_back(i)，但是這樣太大，
          而且不是每對f1, f2都有公共點，就用了map，二分查詢。
*/
#pragma comment(linker, "/STACK:102400000,102400000")
#include <stdio.h>
#include <algorithm>
#include <iostream>
#include <string.h>
#include <vector>
#include <map>
using namespace std;
const int maxn=100500;

int n,m;
vector<int>vec[2][maxn];
int fa[2][maxn],dep[2][maxn],siz[2][maxn],top[2][maxn],son[2][maxn];
map<pair<int,int>,int>mp;
vector<pair<int,int> >ans;
vector<pair<int,int> >::iterator lv[maxn],rv[maxn];

void init()
{
    for(int i=0;i<=n;i++)
    {
        vec[0][i].clear();
        vec[1][i].clear();
    }
    mp.clear();
    ans.clear();
}

void dfs1(int u,int pre,int flag)
{
    son[flag][u]=0,siz[flag][u]=1;
    dep[flag][u]=dep[flag][pre]+1;
    fa[flag][u]=pre;
    int n=vec[flag][u].size();
    for(int i=0;i<n;i++)
    {
        int v=vec[flag][u][i];
        dfs1(v,u,flag);
        if(siz[flag][son[flag][u]]<siz[flag][v])
        {
            son[flag][u]=v;
        }
        siz[flag][u]+=siz[flag][v];
    }
}

void dfs2(int u,int tp,int flag)
{
    top[flag][u]=tp;
    if(son[flag][u])
    {
        dfs2(son[flag][u],tp,flag);
    }
    int n=vec[flag][u].size();
    for(int i=0;i<n;i++)
    {
        int v=vec[flag][u][i];
        if(v==son[flag][u])continue;
        dfs2(v,v,flag);
    }
}

int solve(int x,int y)///分別列舉x和y的所在鏈，找深度最大的同號頂點
{
    int fai,faj;
    for(int i=x;i;i=fa[0][fai])
    {
        fai=top[0][i];
        for(int j=y;j;j=fa[1][faj])
        {
            faj=top[1][j];
            if(j<fai)break;
            if(i<faj)continue;
            int t=mp[make_pair(fai,faj)];
            if(t==0)continue;
            if((rv[t]-1)->second<=min(i,j))
                return (rv[t]-1)->second;
            else
            {
                vector<pair<int,int> >::iterator id=upper_bound(lv[t],rv[t],make_pair(t,min(i,j)));
                if(id!=lv[t])return (id-1)->second;
            }
        }
    }
}
int main()
{
     while(~scanf("%d%d",&n,&m))
     {
         init();
         for(int i=1;i<n;i++)///wife tree
         {
             int x;
             scanf("%d",&x);
             vec[0][x].push_back(i+1);
         }
         for(int i=1;i<n;i++)///husband tree
         {
             int x;
             scanf("%d",&x);
             vec[1][x].push_back(i+1);
         }
         for(int i=0;i<2;i++)///分別進行樹鏈剖分
         {
             dep[i][0]=0;
             dfs1(1,0,i);
             dfs2(1,1,i);
         }
         int cnt=0;
         for(int i=1;i<=n;i++)///記錄每一個節點在兩個樹中鏈的位置
         {
             pair<int,int> tmp=make_pair(top[0][i],top[1][i]);
             if(mp[tmp]==0)mp[tmp]=++cnt;
             ans.push_back(make_pair(mp[tmp],i));
         }
         sort(ans.begin(),ans.end());
         for(int i=1;i<=cnt;i++)
         {
             lv[i]=lower_bound(ans.begin(),ans.end(),make_pair(i,0));
             rv[i]=upper_bound(ans.begin(),ans.end(),make_pair(i,n));
         }
         int pre=0;
         while(m--)
         {
             int x,y;
             scanf("%d%d",&x,&y);
             x=(x+pre)%n+1;
             y=(y+pre)%n+1;
             int ret=solve(x,y);
             int ret1=abs(dep[0][x]-dep[0][ret])+1;
             int ret2=abs(dep[1][y]-dep[1][ret])+1;
             pre=ret;
             printf("%d %d %d\n",ret,ret1,ret2);
         }
     }
     return 0;
}


相關文章