hdu 4568 spfa 最短路演算法+旅行商問題
http://acm.hdu.edu.cn/showproblem.php?pid=4568
Problem Description
One day, a hunter named James went to a mysterious area to find the treasures. James wanted to research the area and brought all treasures that he could.
The area can be represented as a N*M rectangle. Any points of the rectangle is a number means the cost of research it,-1 means James can't cross it, James can start at any place out of the rectangle, and explore point next by next. He will move in the rectangle and bring out all treasures he can take. Of course, he will end at any border to go out of rectangle(James will research every point at anytime he cross because he can't remember whether the point are researched or not).
Now give you a map of the area, you must calculate the least cost that James bring out all treasures he can take(one point up to only one treasure).Also, if nothing James can get, please output 0.
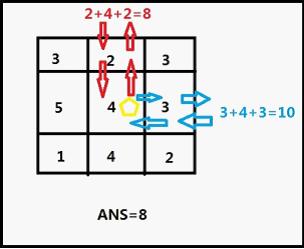
The area can be represented as a N*M rectangle. Any points of the rectangle is a number means the cost of research it,-1 means James can't cross it, James can start at any place out of the rectangle, and explore point next by next. He will move in the rectangle and bring out all treasures he can take. Of course, he will end at any border to go out of rectangle(James will research every point at anytime he cross because he can't remember whether the point are researched or not).
Now give you a map of the area, you must calculate the least cost that James bring out all treasures he can take(one point up to only one treasure).Also, if nothing James can get, please output 0.

Input
The input consists of T test cases. The number of test cases T is given in the first line of the input. Each test case begins with a line containing 2 integers N M , (1<=N,M<=200), that represents the rectangle. Each of the following N lines contains M numbers(0~9),represent
the cost of each point. Next is K(1<=K<=13),and next K lines, each line contains 2 integers x y means the position of the treasures, x means row and start from 0, y means column start from 0 too.
Output
For each test case, you should output only a number means the minimum cost.
Sample Input
2
3 3
3 2 3
5 4 3
1 4 2
1
1 1
3 3
3 2 3
5 4 3
1 4 2
2
1 1
2 2
Sample Output
8
11
/**
hdu 4568 spfa 最短路演算法+旅行商問題
題目大意:給定一個n*m的棋盤,每一個格子有一個值,代表經過這個格子的花費,給出sum個寶藏點的座標,求從棋盤的任意一個邊進入棋盤,經過所有的寶藏點後在走出
棋盤所需要的最小花費
解題思路:spfa處理處任意兩個寶藏點之間的最短距離(最小花費)和每個寶藏點和邊界的最短距離。然後狀態壓縮:dp[s][i]表示經過寶藏點的狀態為s並且結尾點為i的
最小花費
*/
#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <iostream>
#include <queue>
using namespace std;
const int maxn=205;
int n,m;
struct note
{
int x,y;
} point[15];
int dx[4][2]= {1,0,0,1,-1,0,0,-1};
int dis[maxn][maxn],a[maxn][maxn],dis_border[25],length[20][20];
bool vis[maxn][maxn];
int dp[1<<15][15];
void spfa(int s)
{
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
dis[i][j]=0x3f3f3f3f;
memset(vis,0,sizeof(vis));
queue<pair<int,int> >q;
q.push(make_pair(point[s].x,point[s].y));
vis[point[s].x][point[s].y]=1;
dis[point[s].x][point[s].y]=0;
while(!q.empty())
{
int x=q.front().first;
int y=q.front().second;
q.pop();
vis[x][y]=0;
if(x==0||x==n-1||y==0||y==m-1)
dis_border[s]=min(dis_border[s],dis[x][y]);
for(int i=0; i<4; i++)
{
int xx=x+dx[i][0];
int yy=y+dx[i][1];
if(xx>=0&&xx<n&&yy>=0&&yy<m&&a[xx][yy]!=-1)
{
if(dis[xx][yy]>dis[x][y]+a[xx][yy])
{
dis[xx][yy]=dis[x][y]+a[xx][yy];
if(vis[xx][yy]==0)
{
vis[xx][yy]=1;
q.push(make_pair(xx,yy));
}
}
}
}
}
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
scanf("%d%d",&n,&m);
for(int i=0; i<n; i++)
{
for(int j=0; j<m; j++)
{
scanf("%d",&a[i][j]);
}
}
int k;
scanf("%d\n",&k);
for(int i=0;i<k;i++)
{
scanf("%d%d",&point[i].x,&point[i].y);
}
//===預處理===
for(int i=0;i<k;i++)
{
dis_border[i]=0x3f3f3f3f;
for(int j=0;j<k;j++)
{
if(i==j)
length[i][j]=0;
else
length[i][j]=0x3f3f3f3f;
}
}
for(int i=0;i<(1<<k);i++)
{
for(int j=0;j<k;j++)
{
dp[i][j]=0x3f3f3f3f;
}
}
//===求有寶藏的點之間和每一個寶藏點和邊界的最短距離===
for(int i=0; i<k; i++)
{
spfa(i);
for(int j=0; j<k; j++)
{
if(j==i)continue;
length[i][j]=min(dis[point[j].x][point[j].y],length[i][j]);
}
dp[1<<i][i]=dis_border[i]+a[point[i].x][point[i].y];
}
///===求最優路徑===
for(int s=0;s<(1<<k);s++)
{
for(int i=0;i<k;i++)
{
if(s&(1<<i)==0)continue;
if(dp[s][i]==0x3f3f3f3f)continue;
for(int j=0;j<k;j++)
{
if(s&(1<<j)==1)continue;
dp[s|(1<<j)][j]=min(dp[s|(1<<j)][j],dp[s][i]+length[i][j]);
}
}
}
///===還要回到邊界==
int ans=0x3f3f3f3f;
for(int i=0;i<k;i++)
{
ans=min(ans,dp[(1<<k)-1][i]+dis_border[i]);
}
printf("%d\n",ans);
}
return 0;
}
相關文章
- 最短路-SPFA演算法&Floyd演算法演算法
- HDU3790 最短路徑問題【Dijkstra演算法】演算法
- 最短路演算法詳解(Dijkstra/SPFA/Floyd)演算法
- POJ 1511 Invitation Cards(最短路spfa演算法)演算法
- 演算法:最短路徑問題演算法
- 最短路(DJsktra,spfa,flyd).mdJS
- 演算法專題 | 10行程式碼實現的最短路演算法——Bellman-ford與SPFA演算法行程
- HDU 4460 Friend Chains(map + spfa)AI
- 最短路徑問題 (dijkstra演算法)演算法
- Bellmanford與Spfa解決存在負邊權的單源匯最短路問題
- HDU 3068 最長迴文(Manacher演算法解決最長迴文串問題)演算法
- 851. spfa求最短路(用佇列優化bellman——ford演算法)佇列優化演算法
- SPFA演算法演算法
- 遺傳演算法解決旅行商問題(TSP)演算法
- 使用A*演算法解迷宮最短路徑問題演算法
- 最短路徑問題
- hdu1874 暢通工程續 Bellman-Ford演算法SPFA演算法
- ACO蟻群演算法解決TSP旅行商問題演算法
- 蟻群演算法實現TSP(旅行商)問題(java)演算法Java
- 旅行商問題(TSP)概述
- HDU3665Seaside(最短路徑)IDE
- python實現Dijkstra演算法之 最短路徑問題Python演算法
- 模擬退火演算法Python程式設計(4)旅行商問題演算法Python程式設計
- SPFA演算法模板(C/C++)演算法C++
- [最短路徑問題]Dijkstra演算法(含還原具體路徑)演算法
- HDU 5067 Harry And Dig Machine:TSP(旅行商)Mac
- 最短路演算法演算法
- week2 kuangbin 題單 最短路問題 + 並查集問題並查集
- hdu5090 匈牙利演算法二分圖最大匹配問題演算法
- 2013成都站D題||hdu4784 bfs+DP+priority_queue(思路從spfa得到啟示)
- Bellman - Ford, SPFA 學習筆記(含有負權的單源最短路徑)筆記
- P1354 房間最短路問題
- hdu2048遞迴問題遞迴
- hdu2049遞迴問題遞迴
- Floyd最短路演算法演算法
- 最短路徑演算法演算法
- 《迷茫的旅行商:一個無處不在的計算機演算法問題》很好看計算機演算法
- hdu5365 簡單幾何問題