2013南京站I題||hdu4810 二進位制列舉
http://acm.hdu.edu.cn/showproblem.php?pid=4810
Problem Description
Ms.Fang loves painting very much. She paints GFW(Great Funny Wall) every day. Every day before painting, she produces a wonderful color of pigments by mixing water and some bags of pigments. On the K-th day, she will select K specific bags of pigments and mix
them to get a color of pigments which she will use that day. When she mixes a bag of pigments with color A and a bag of pigments with color B, she will get pigments with color A xor B.
When she mixes two bags of pigments with the same color, she will get color zero for some strange reasons. Now, her husband Mr.Fang has no idea about which K bags of pigments Ms.Fang will select on the K-th day. He wonders the sum of the colors Ms.Fang will get with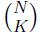 different plans.
different plans.
For example, assume n = 3, K = 2 and three bags of pigments with color 2, 1, 2. She can get color 3, 3, 0 with 3 different plans. In this instance, the answer Mr.Fang wants to get on the second day is 3 + 3 + 0 = 6.
Mr.Fang is so busy that he doesn’t want to spend too much time on it. Can you help him?
You should tell Mr.Fang the answer from the first day to the n-th day.
When she mixes two bags of pigments with the same color, she will get color zero for some strange reasons. Now, her husband Mr.Fang has no idea about which K bags of pigments Ms.Fang will select on the K-th day. He wonders the sum of the colors Ms.Fang will get with
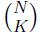 different plans.
different plans.For example, assume n = 3, K = 2 and three bags of pigments with color 2, 1, 2. She can get color 3, 3, 0 with 3 different plans. In this instance, the answer Mr.Fang wants to get on the second day is 3 + 3 + 0 = 6.
Mr.Fang is so busy that he doesn’t want to spend too much time on it. Can you help him?
You should tell Mr.Fang the answer from the first day to the n-th day.
Input
There are several test cases, please process till EOF.
For each test case, the first line contains a single integer N(1 <= N <= 103).The second line contains N integers. The i-th integer represents the color of the pigments in the i-th bag.
For each test case, the first line contains a single integer N(1 <= N <= 103).The second line contains N integers. The i-th integer represents the color of the pigments in the i-th bag.
Output
For each test case, output N integers in a line representing the answers(mod 106 +3) from the first day to the n-th day.
Sample Input
4
1 2 10 1
Sample Output
14 36 30 8
一開始拿到這個題感覺有點摸不著頭腦,最笨的方法是列舉出所有的種類一個一個的進行異或,但是馬上就想到這個方法根本就行不通,先不說超時的問題,就是組合數在longlong範圍內就根本不可能取得到。
似乎這個題沒有什麼解法了,但是仔細想想,根異或的特性,對於每一個二進位制位我們只有當1的個數為奇數的時候才可能通過異或在該位得到1。因此,我們可以列舉所有二進位制位,計算出每個二進位制位上1的個數k,我們列舉1~k之間所有的奇數(1,3,5,7……),利用組合數求出各種取法的和然後乘上權值1<<i。
想到這裡,緊接著又出現了一個新的問題,就是求得的和是否等於所求呢?只是列舉的單個位數,我們在取得時候可是要整取的啊?可以這樣想,在整取的過程中,把所有的情況全列舉出來之後做異或時還是要各個位單獨異或,相互之間沒有影響,最後在做完還是要加起來。傳統的過程與我們的做法唯一不同的是:他是把一個數的各個二進位制位計算出後相加從而得到一個新的數,然後和其他情況計算出的數進行相加取和。而我們是把所有情況中相同的二進位制位先相加,然後在對所有的二進位制位進行求和。過程不一樣,其結果是一致的。問題分析到這裡基本上就可以收尾了,下面就是程式碼實現了
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int MOD=1000003;
const int N=1005;
int n,c[N][N],a[N];
int ans[N];
void init()//預處理,先求出組合數
{
memset(c,0,sizeof(c));
for(int i=0;i<N;i++)
{
c[i][0]=1;
for(int j=1;j<=i;j++)
c[i][j]=(c[i-1][j]+c[i-1][j-1])%MOD;
}
/*for(int i=0;i<=10;i++)
{
for(int j=0;j<=i;j++)
printf("%d ",c[i][j]);
printf("\n");
}*/
}
void get(int n)//統計各個二進位制位上有多少個1
{
for(int i=0;i<32;i++)
{
if(n&(1<<i))
a[i]++;
}
}
int main()
{
init();
while(~scanf("%d",&n))
{
int temp;
memset(a,0,sizeof(a));
for(int i=0;i<n;i++)
{
scanf("%d",&temp);
get(temp);
}
memset(ans,0,sizeof(ans));
for(int i=1;i<=n;i++)//1~n的所有情況
for(int j=0;j<32;j++)//所有的二進位制位。題目給出數最大不過1000000+3,32位足矣
for(int k=1;k<=a[j]&&k<=i;k+=2)//從1~a[j]列舉出所有的奇數情況,並且還要保證不能超過i
ans[i]=(ans[i]+(LL)c[a[j]][k]*c[n-a[j]][i-k]%MOD*(1<<j%MOD)%MOD)%MOD;//這裡的中間過程會爆掉int,需要強制轉換一下子
for(int i=1;i<=n;i++)
printf(i==n?"%d\n":"%d ",ans[i]);
}
return 0;
}
相關文章
- 二進位制陣列陣列
- HDU 4937 Lucky Number(列舉進位制)
- HDU 4135——Co-prime(容斥原理&&二進位制列舉)
- 二進位制陣列 subarray() 方法陣列
- 二進位制與二進位制運算
- 二進位制陣列 buffer 屬性陣列
- 二進位制陣列 length 屬性陣列
- 進位制詳解:二進位制、八進位制和十六進位制
- JavaScript 二進位制、八進位制與十六進位制JavaScript
- (二進位制)
- 二進位制
- 十進位制——二 (八、十六 )進位制
- JavaScript二進位制陣列建立注意點JavaScript陣列
- 二進位制陣列 byteLength 屬性陣列
- 二進位制陣列 byteOffset 屬性陣列
- 二進位制,八進位制,十進位制,十六進位制的相互轉換
- 【進位制轉換】二進位制、十六進位制、十進位制、八進位制對應關係
- 二進位制、十進位制與十六進位制相互轉化
- 2020東北林業大學acm集訓第五天 二進位制操作與二進位制列舉(附相關習題及AC程式碼)ACMC程式
- java中二進位制、八進位制、十進位制、十六進位制的轉換Java
- 二進位制,八進位制,十進位制,十六進位制之間的轉換
- Python 進位制互相轉換(二進位制、十進位制和十六進位制)Python
- 計算機基礎進位制轉換(二進位制、八進位制、十進位制、十六進位制)計算機
- 二進位制轉十進位制快速方法
- JAVA 二進位制,八進位制,十六進位制,十進位制間進行相互轉換Java
- 什麼是二進位制?二進位制如何轉換?
- 數字邏輯練習題-(二進位制/16進位制模擬)
- 方格分割 二進位制列舉+DFS(2017 第八屆藍橋杯省賽A組 第4題)
- 04 二進位制
- 大話二進位制,八進位制,十進位制,十六進位制之間的轉換
- 資訊學奧賽初賽天天練-71-NOIP2016普及組-基礎題2-進位制轉換、二進位制轉八進位制、八進位制轉二進位制、二叉樹陣列儲存、定址空間二叉樹陣列
- JavaScript十進位制轉換為二進位制JavaScript
- Oracle二進位制與十進位制轉換Oracle
- 十進位制轉二進位制推導(草稿)
- [計算機基礎] 計算機進位制轉換:二進位制、八進位制、十進位制、十六進位制計算機
- 一看就懂二進位制、八進位制、十六進位制數轉換十進位制
- python進位制轉換(二進位制、十進位制和十六進位制)及注意事項Python
- Oracle中的二進位制、八進位制、十進位制、十六進位制相互轉換函式Oracle函式