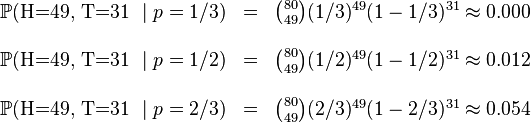【機器學習演算法-python實現】最大似然估計(Maximum Likelihood)
1.背景
最大似然估計是概率論中常常涉及到的一種統計方法。大體的思想是,在知道概率密度f的前提下,我們進行一次取樣,就可以根據f來計算這個取樣實現的可能性。當然最大似然可以有很多變化,這裡實現一種簡單的,實際專案需要的時候可以再更改。
博主是參照wiki來學習的,地址請點選我
這裡實現的是特別簡單的例子如下(摘自wiki的最大似然)
離散分佈,離散有限引數空間[編輯]
考慮一個拋硬幣的例子。假設這個硬幣正面跟反面輕重不同。我們把這個硬幣拋80次(即,我們獲取一個取樣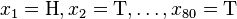 並把正面的次數記下來,正面記為H,反面記為T)。並把丟擲一個正面的概率記為
並把正面的次數記下來,正面記為H,反面記為T)。並把丟擲一個正面的概率記為 ,丟擲一個反面的概率記為
,丟擲一個反面的概率記為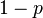 (因此,這裡的
(因此,這裡的 即相當於上邊的
即相當於上邊的 )。假設我們丟擲了49個正面,31個反面,即49次H,31次T。假設這個硬幣是我們從一個裝了三個硬幣的盒子裡頭取出的。這三個硬幣丟擲正面的概率分別為
)。假設我們丟擲了49個正面,31個反面,即49次H,31次T。假設這個硬幣是我們從一個裝了三個硬幣的盒子裡頭取出的。這三個硬幣丟擲正面的概率分別為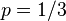 ,
, 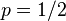 ,
,  .這些硬幣沒有標記,所以我們無法知道哪個是哪個。使用最大似然估計,通過這些試驗資料(即取樣資料),我們可以計算出哪個硬幣的可能性最大。這個似然函式取以下三個值中的一個:
.這些硬幣沒有標記,所以我們無法知道哪個是哪個。使用最大似然估計,通過這些試驗資料(即取樣資料),我們可以計算出哪個硬幣的可能性最大。這個似然函式取以下三個值中的一個:
我們可以看到當 時,似然函式取得最大值。這就是
時,似然函式取得最大值。這就是 的最大似然估計。
的最大似然估計。
2.實現部分
有一點要提的是,因為用到了階乘,關於階乘問題本來想到的方法是用遞迴來實現。但是google了一下發現其實python的reduce方法用起來更加方便,一句話就解決的。
def Factorial(x):
return reduce(lambda x,y:x*y,range(1,x+1)) 完整工程:
'''
Created on 2014-8-22
@author: Garvin
Maximum Likelihood theory practic
This code is base on the http://zh.wikipedia.org/wiki/%E6%9C%80%E5%A4%A7%E4%BC%BC%E7%84%B6%E4%BC%B0%E8%AE%A1
'''
w=2.0/3
h=49
t=31
def DefineParam():
H=h
T=t
return H,T
def MaximumLikelihood(p=w):
H,T=DefineParam()
f1=Factorial(H+T)/(Factorial(H)*Factorial(T))
f2=(p**H)*((1.0-p)**T)
return f1*f2
def Factorial(x):
return reduce(lambda x,y:x*y,range(1,x+1))
實現效果,對應上面的例子,當H=49,T=31,是P=2/3概率的可能性

程式碼地址:請點選我
/********************************
* 本文來自部落格 “李博Garvin“
* 轉載請標明出處:http://blog.csdn.net/buptgshengod
******************************************/
相關文章
- 似然函式與最大似然估計函式
- 機器學習必知概念:貝葉斯估計、最大似然估計、最大後驗估計機器學習
- 最大似然估計詳解
- 從最大似然估計開始,你需要打下的機器學習基石機器學習
- 01EM演算法-大綱-最大似然估計(MLE)、貝葉斯演算法估計、最大後驗概率估計(MAP)演算法
- [筆記]極大似然估計、最大後驗概率、貝葉斯估計筆記
- 詳解最大似然估計(MLE)、最大後驗概率估計(MAP),以及貝葉斯公式的理解公式
- 機器學習系列文章:引數方法(最大似然、分類)機器學習
- 從最大似然到EM演算法淺解演算法
- 極大似然估計理解與應用
- 【機器學習】【邏輯迴歸】代價函式為什麼用最大似然估計而不是最小二乘法?機器學習邏輯迴歸函式
- 基於極大似然估計方法的diffusion
- 機器學習--白板推導系列筆記2 概率:高斯分佈之極大似然估計機器學習筆記
- 最大似然函式和最大後驗概率區別函式
- 淺議極大似然估計(MLE)背後的思想原理
- 如何通俗地理解概率論中的「極大似然估計法」?
- 從DDPM到DDIM (一) 極大似然估計與證據下界
- 從極大似然估計的角度理解深度學習中loss函式深度學習函式
- 損失函式:最小二乘法與極大似然估計法函式
- 【小白學AI】線性迴歸與邏輯迴歸(似然引數估計)AI邏輯迴歸
- 機器學習 - 似然函式:概念、應用與程式碼例項機器學習函式
- 機器學習之kNN演算法(純python實現)機器學習KNN演算法Python
- Python實現常見機器學習演算法(上)Python機器學習演算法
- k近鄰演算法python實現 -- 《機器學習實戰》演算法Python機器學習
- 幽默:駭客式程式設計其實類似機器學習!程式設計機器學習
- 機器學習10種經典演算法的Python實現機器學習演算法Python
- 【機器學習PAI實踐八】用機器學習演算法評估學生考試成績機器學習AI演算法
- 樸素貝葉斯演算法的python實現 -- 機器學習實戰演算法Python機器學習
- 決策樹ID3演算法python實現 -- 《機器學習實戰》演算法Python機器學習
- 機器學習之k-means聚類演算法(python實現)機器學習聚類演算法Python
- 《機器學習實戰》k最近鄰演算法(K-Nearest Neighbor,Python實現)機器學習演算法RESTPython
- 數學推導+Python實現機器學習演算法:線性迴歸Python機器學習演算法
- 為什麼要選擇Python語言實現機器學習演算法Python機器學習演算法
- Python 實現任意多邊形的最大內切圓演算法_任意多邊形最大內切圓演算法Python演算法
- 機器學習分享——KNN演算法及numpy實現機器學習KNN演算法
- 基於似然場的全域性定位
- 演算法金 | 必會的機器學習評估指標演算法機器學習指標
- 數學推導+純Python實現機器學習演算法:邏輯迴歸Python機器學習演算法邏輯迴歸