教你如何迅速秒殺掉：99%的海量資料處理面試題

http://blog.csdn.net/v_july_v/article/details/7382693

      教你如何迅速秒殺掉：99%的海量資料處理面試題

作者：July
出處：結構之法演算法之道blog

前言

   一般而言，標題含有“秒殺”，“99%”，“史上最全/最強”等詞彙的往往都脫不了譁眾取寵之嫌，但進一步來講，如果讀者讀罷此文，卻無任何收穫，那麼，我也甘願揹負這樣的罪名，:-)，同時，此文可以看做是對這篇文章：十道海量資料處理面試題與十個方法大總結的一般抽象性總結。

    畢竟受文章和理論之限，本文將摒棄絕大部分的細節，只談方法/模式論，且注重用最通俗最直白的語言闡述相關問題。最後，有一點必須強調的是，全文行文是基於面試題的分析基礎之上的，具體實踐過程中，還是得具體情況具體分析，且各個場景下需要考慮的細節也遠比本文所描述的任何一種解決方法複雜得多。

    OK，若有任何問題，歡迎隨時不吝賜教。謝謝。

何謂海量資料處理？

   所謂海量資料處理，無非就是基於海量資料上的儲存、處理、操作。何謂海量，就是資料量太大，所以導致要麼是無法在較短時間內迅速解決，要麼是資料太大，導致無法一次性裝入記憶體。

    那解決辦法呢?針對時間，我們可以採用巧妙的演算法搭配合適的資料結構，如Bloom filter/Hash/bit-map/堆/資料庫或倒排索引/trie樹，針對空間，無非就一個辦法：大而化小，分而治之（hash對映），你不是說規模太大嘛，那簡單啊，就把規模大化為規模小的，各個擊破不就完了嘛。

    至於所謂的單機及叢集問題，通俗點來講，單機就是處理裝載資料的機器有限(只要考慮cpu，記憶體，硬碟的資料互動)，而叢集，機器有多輛，適合分散式處理，平行計算(更多考慮節點和節點間的資料互動)。

    再者，通過本blog內的有關海量資料處理的文章：Big Data Processing，我們已經大致知道，處理海量資料問題，無非就是：

1. 分而治之/hash對映 + hash統計 + 堆/快速/歸併排序；
2. 雙層桶劃分
3. Bloom filter/Bitmap；
4. Trie樹/資料庫/倒排索引；
5. 外排序；
6. 分散式處理之Hadoop/Mapreduce。

    下面，本文第一部分、從set/map談到hashtable/hash_map/hash_set，簡要介紹下set/map/multiset/multimap，及hash_set/hash_map/hash_multiset/hash_multimap之區別(萬丈高樓平地起，基礎最重要)，而本文第二部分，則針對上述那6種方法模式結合對應的海量資料處理面試題分別具體闡述。

第一部分、從set/map談到hashtable/hash_map/hash_set

    稍後本文第二部分中將多次提到hash_map/hash_set，下面稍稍介紹下這些容器，以作為基礎準備。一般來說，STL容器分兩種，

• 序列式容器(vector/list/deque/stack/queue/heap)，
• 關聯式容器。關聯式容器又分為set(集合)和map(對映表)兩大類，以及這兩大類的衍生體multiset(多鍵集合)和multimap(多鍵對映表)，這些容器均以RB-tree完成。此外，還有第3類關聯式容器，如hashtable(雜湊表)，以及以hashtable為底層機制完成的hash_set(雜湊集合)/hash_map(雜湊對映表)/hash_multiset(雜湊多鍵集合)/hash_multimap(雜湊多鍵對映表)。也就是說，set/map/multiset/multimap都內含一個RB-tree，而hash_set/hash_map/hash_multiset/hash_multimap都內含一個hashtable。

    所謂關聯式容器，類似關聯式資料庫，每筆資料或每個元素都有一個鍵值(key)和一個實值(value)，即所謂的Key-Value(鍵-值對)。當元素被插入到關聯式容器中時，容器內部結構(RB-tree/hashtable)便依照其鍵值大小，以某種特定規則將這個元素放置於適當位置。

     包括在非關聯式資料庫中，比如，在MongoDB內，文件(document)是最基本的資料組織形式，每個文件也是以Key-Value（鍵-值對）的方式組織起來。一個文件可以有多個Key-Value組合，每個Value可以是不同的型別，比如String、Integer、List等等。 
{ "name" : "July",  
  "sex" : "male",  
    "age" : 23 }  

set/map/multiset/multimap

    set，同map一樣，所有元素都會根據元素的鍵值自動被排序，因為set/map兩者的所有各種操作，都只是轉而呼叫RB-tree的操作行為，不過，值得注意的是，兩者都不允許兩個元素有相同的鍵值。
    不同的是：set的元素不像map那樣可以同時擁有實值(value)和鍵值(key)，set元素的鍵值就是實值，實值就是鍵值，而map的所有元素都是pair，同時擁有實值(value)和鍵值(key)，pair的第一個元素被視為鍵值，第二個元素被視為實值。
    至於multiset/multimap，他們的特性及用法和set/map完全相同，唯一的差別就在於它們允許鍵值重複，即所有的插入操作基於RB-tree的insert_equal()而非insert_unique()。

hash_set/hash_map/hash_multiset/hash_multimap

    hash_set/hash_map，兩者的一切操作都是基於hashtable之上。不同的是，hash_set同set一樣，同時擁有實值和鍵值，且實質就是鍵值，鍵值就是實值，而hash_map同map一樣，每一個元素同時擁有一個實值(value)和一個鍵值(key)，所以其使用方式，和上面的map基本相同。但由於hash_set/hash_map都是基於hashtable之上，所以不具備自動排序功能。為什麼?因為hashtable沒有自動排序功能。
    至於hash_multiset/hash_multimap的特性與上面的multiset/multimap完全相同，唯一的差別就是它們hash_multiset/hash_multimap的底層實現機制是hashtable（而multiset/multimap，上面說了，底層實現機制是RB-tree），所以它們的元素都不會被自動排序，不過也都允許鍵值重複。

    所以，綜上，說白了，什麼樣的結構決定其什麼樣的性質，因為set/map/multiset/multimap都是基於RB-tree之上，所以有自動排序功能，而hash_set/hash_map/hash_multiset/hash_multimap都是基於hashtable之上，所以不含有自動排序功能，至於加個字首multi_無非就是允許鍵值重複而已。

    此外，

• 關於什麼hash，請看blog內此篇文章；
• 關於紅黑樹，請參看blog內系列文章，
• 關於hash_map的具體應用：請看這裡，關於hash_set：請看此文。

    OK，接下來，請看本文第二部分、處理海量資料問題之六把密匙。

第二部分、處理海量資料問題之六把密匙

密匙一、分而治之/Hash對映 + Hash_map統計 + 堆/快速/歸併排序

   具體而論，則是： “首先是這一天，並且是訪問百度的日誌中的IP取出來，逐個寫入到一個大檔案中。注意到IP是32位的，最多有個2^32個IP。同樣可以採用對映的方法，比如%1000，把整個大檔案對映為1000個小檔案，再找出每個小文中出現頻率最大的IP（可以採用hash_map對那1000個檔案中的所有IP進行頻率統計，然後依次找出各個檔案中頻率最大的那個IP）及相應的頻率。然後再在這1000個最大的IP中，找出那個頻率最大的IP，即為所求。”--十道海量資料處理面試題與十個方法大總結。

    關於本題，還有幾個問題，如下：

      1、Hash取模是一種等價對映，不會存在同一個元素分散到不同小檔案中去的情況，即這裡採用的是mod1000演算法，那麼相同的IP在hash後，只可能落在同一個檔案中，不可能被分散的。
      2、那到底什麼是hash對映呢？簡單來說，就是為了便於計算機在有限的記憶體中處理big資料，從而通過一種對映雜湊的方式讓資料均勻分佈在對應的記憶體位置(如大資料通過取餘的方式對映成小樹存放在記憶體中，或大檔案對映成多個小檔案)，而這個對映雜湊方式便是我們通常所說的hash函式，設計的好的hash函式能讓資料均勻分佈而減少衝突。儘管資料對映到了另外一些不同的位置，但資料還是原來的資料，只是代替和表示這些原始資料的形式發生了變化而已。

    OK，有興趣的，還可以再瞭解下一致性hash演算法，見blog內此文第五部分：http://blog.csdn.net/v_july_v/article/details/6879101。

2、尋找熱門查詢，300萬個查詢字串中統計最熱門的10個查詢

    原題：搜尋引擎會通過日誌檔案把使用者每次檢索使用的所有檢索串都記錄下來，每個查詢串的長度為1-255位元組。假設目前有一千萬個記錄（這些查詢串的重複度比較高，雖然總數是1千萬，但如果除去重複後，不超過3百萬個。一個查詢串的重複度越高，說明查詢它的使用者越多，也就是越熱門），請你統計最熱門的10個查詢串，要求使用的記憶體不能超過1G。

    解答：由上面第1題，我們知道，資料大則劃為小的，如如一億個Ip求Top 10，可先%1000將ip分到1000個小檔案中去，並保證一種ip只出現在一個檔案中，再對每個小檔案中的ip進行hashmap計數統計並按數量排序，最後歸併或者最小堆依次處理每個小檔案的top10以得到最後的結。

    但如果資料規模比較小，能一次性裝入記憶體呢?比如這第2題，雖然有一千萬個Query，但是由於重複度比較高，因此事實上只有300萬的Query，每個Query255Byte，因此我們可以考慮把他們都放進記憶體中去（300萬個字串假設沒有重複，都是最大長度，那麼最多佔用記憶體3M*1K/4=0.75G。所以可以將所有字串都存放在記憶體中進行處理），而現在只是需要一個合適的資料結構，在這裡，HashTable絕對是我們優先的選擇。

    所以我們放棄分而治之/hash對映的步驟，直接上hash統計，然後排序。So，針對此類典型的TOP K問題，採取的對策往往是：hashmap + 堆。如下所示：

1. hash_map統計：先對這批海量資料預處理。具體方法是：維護一個Key為Query字串，Value為該Query出現次數的HashTable，即hash_map(Query，Value)，每次讀取一個Query，如果該字串不在Table中，那麼加入該字串，並且將Value值設為1；如果該字串在Table中，那麼將該字串的計數加一即可。最終我們在O(N)的時間複雜度內用Hash表完成了統計；
2. 堆排序：第二步、藉助堆這個資料結構，找出Top K，時間複雜度為N‘logK。即藉助堆結構，我們可以在log量級的時間內查詢和調整/移動。因此，維護一個K(該題目中是10)大小的小根堆，然後遍歷300萬的Query，分別和根元素進行對比。所以，我們最終的時間複雜度是：O（N） + N' * O（logK），（N為1000萬，N’為300萬）。

    別忘了這篇文章中所述的堆排序思路：“維護k個元素的最小堆，即用容量為k的最小堆儲存最先遍歷到的k個數，並假設它們即是最大的k個數，建堆費時O（k），並調整堆(費時O（logk）)後，有k1>k2>...kmin（kmin設為小頂堆中最小元素）。繼續遍歷數列，每次遍歷一個元素x，與堆頂元素比較，若x>kmin，則更新堆（x入堆，用時logk），否則不更新堆。這樣下來，總費時O（k*logk+（n-k）*logk）=O（n*logk）。此方法得益於在堆中，查詢等各項操作時間複雜度均為logk。”--第三章續、Top K演算法問題的實現。
    當然，你也可以採用trie樹，關鍵字域存該查詢串出現的次數，沒有出現為0。最後用10個元素的最小推來對出現頻率進行排序。

3、有一個1G大小的一個檔案，裡面每一行是一個詞，詞的大小不超過16位元組，記憶體限制大小是1M。返回頻數最高的100個詞。
       由上面那兩個例題，分而治之 + hash統計 + 堆/快速排序這個套路，我們已經開始有了屢試不爽的感覺。下面，再拿幾道再多多驗證下。請看此第3題：又是檔案很大，又是記憶體受限，咋辦?還能怎麼辦呢?無非還是：

1. 分而治之/hash對映：順序讀檔案中，對於每個詞x，取hash(x)%5000，然後按照該值存到5000個小檔案（記為x0,x1,...x4999）中。這樣每個檔案大概是200k左右。如果其中的有的檔案超過了1M大小，還可以按照類似的方法繼續往下分，直到分解得到的小檔案的大小都不超過1M。
2. hash_map統計：對每個小檔案，採用trie樹/hash_map等統計每個檔案中出現的詞以及相應的頻率。
3. 堆/歸併排序：取出出現頻率最大的100個詞（可以用含100個結點的最小堆）後，再把100個詞及相應的頻率存入檔案，這樣又得到了5000個檔案。最後就是把這5000個檔案進行歸併（類似於歸併排序）的過程了。

    但如果同一個元素重複出現在不同的電腦中呢，如下例子所述：

   方案1：直接上：

1. hash對映：順序讀取10個檔案，按照hash(query)%10的結果將query寫入到另外10個檔案（記為a0,a1,..a9）中。這樣新生成的檔案每個的大小大約也1G（假設hash函式是隨機的）。
2. hash_map統計：找一臺記憶體在2G左右的機器，依次對用hash_map(query, query_count)來統計每個query出現的次數。注：hash_map(query,query_count)是用來統計每個query的出現次數，不是儲存他們的值，出現一次，則count+1。
3. 堆/快速/歸併排序：利用快速/堆/歸併排序按照出現次數進行排序，將排序好的query和對應的query_cout輸出到檔案中，這樣得到了10個排好序的檔案（記為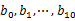）。最後，對這10個檔案進行歸併排序（內排序與外排序相結合）。根據此方案1，這裡有一份實現：https://github.com/ooooola/sortquery/blob/master/querysort.py。

     除此之外，此題還有以下兩個方法：
    方案2：一般query的總量是有限的，只是重複的次數比較多而已，可能對於所有的query，一次性就可以加入到記憶體了。這樣，我們就可以採用trie樹/hash_map等直接來統計每個query出現的次數，然後按出現次數做快速/堆/歸併排序就可以了。

    方案3：與方案1類似，但在做完hash，分成多個檔案後，可以交給多個檔案來處理，採用分散式的架構來處理（比如MapReduce），最後再進行合併。

6、 給定a、b兩個檔案，各存放50億個url，每個url各佔64位元組，記憶體限制是4G，讓你找出a、b檔案共同的url？

    可以估計每個檔案安的大小為5G×64=320G，遠遠大於記憶體限制的4G。所以不可能將其完全載入到記憶體中處理。考慮採取分而治之的方法。

1. 分而治之/hash對映：遍歷檔案a，對每個url求取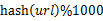，然後根據所取得的值將url分別儲存到1000個小檔案（記為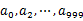，這裡漏寫個了a1）中。這樣每個小檔案的大約為300M。遍歷檔案b，採取和a相同的方式將url分別儲存到1000小檔案中（記為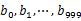）。這樣處理後，所有可能相同的url都在對應的小檔案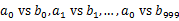（）中，不對應的小檔案不可能有相同的url。然後我們只要求出1000對小檔案中相同的url即可。
2. hash_set統計：求每對小檔案中相同的url時，可以把其中一個小檔案的url儲存到hash_set中。然後遍歷另一個小檔案的每個url，看其是否在剛才構建的hash_set中，如果是，那麼就是共同的url，存到檔案裡面就可以了。

    OK，此第一種方法：分而治之/hash對映 + hash統計 + 堆/快速/歸併排序，再看最後4道題，如下：

7、怎麼在海量資料中找出重複次數最多的一個？

    方案1：先做hash，然後求模對映為小檔案，求出每個小檔案中重複次數最多的一個，並記錄重複次數。然後找出上一步求出的資料中重複次數最多的一個就是所求（具體參考前面的題）。

8、上千萬或上億資料（有重複），統計其中出現次數最多的錢N個資料。

    方案1：上千萬或上億的資料，現在的機器的記憶體應該能存下。所以考慮採用hash_map/搜尋二叉樹/紅黑樹等來進行統計次數。然後就是取出前N個出現次數最多的資料了，可以用第2題提到的堆機制完成。

9、一個文字檔案，大約有一萬行，每行一個詞，要求統計出其中最頻繁出現的前10個詞，請給出思想，給出時間複雜度分析。

     方案1：這題是考慮時間效率。用trie樹統計每個詞出現的次數，時間複雜度是O(n*le)（le表示單詞的平準長度）。然後是找出出現最頻繁的前10個詞，可以用堆來實現，前面的題中已經講到了，時間複雜度是O(n*lg10)。所以總的時間複雜度，是O(n*le)與O(n*lg10)中較大的哪一個。

10. 1000萬字串，其中有些是重複的，需要把重複的全部去掉，保留沒有重複的字串。請怎麼設計和實現？

• 方案1：這題用trie樹比較合適，hash_map也行。
• 方案2：from xjbzju:，1000w的資料規模插入操作完全不現實，以前試過在stl下100w元素插入set中已經慢得不能忍受，覺得基於hash的實現不會比紅黑樹好太多，使用vector+sort+unique都要可行許多，建議還是先hash成小檔案分開處理再綜合。

• 3、那查詢操作呢，如下段文字所述?

    或者小資料量時用map，構造快，大資料量時用hash_map?

rbtree PK hashtable

    據朋友№邦卡貓№的做的紅黑樹和hash table的效能測試中發現：當資料量基本上int型key時，hash table是rbtree的3-4倍，但hash table一般會浪費大概一半記憶體。

    因為hash table所做的運算就是個%，而rbtree要比較很多，比如rbtree要看value的資料 ，每個節點要多出3個指標（或者偏移量） 如果需要其他功能，比如，統計某個範圍內的key的數量，就需要加一個計數成員。

    接下來，我們們來看第二種方法，雙層捅劃分。

密匙二、雙層桶劃分

雙層桶劃分----其實本質上還是分而治之的思想，重在“分”的技巧上！
　　適用範圍：第k大，中位數，不重複或重複的數字
　　基本原理及要點：因為元素範圍很大，不能利用直接定址表，所以通過多次劃分，逐步確定範圍，然後最後在一個可以接受的範圍內進行。可以通過多次縮小，雙層只是一個例子。
　　擴充套件：
　　問題例項：

13、2.5億個整數中找出不重複的整數的個數，記憶體空間不足以容納這2.5億個整數。
    有點像鴿巢原理，整數個數為2^32,也就是，我們可以將這2^32個數，劃分為2^8個區域(比如用單個檔案代表一個區域)，然後將資料分離到不同的區域，然後不同的區域在利用bitmap就可以直接解決了。也就是說只要有足夠的磁碟空間，就可以很方便的解決。

14、5億個int找它們的中位數。

1. 思路一：這個例子比上面那個更明顯。首先我們將int劃分為2^16個區域，然後讀取資料統計落到各個區域裡的數的個數，之後我們根據統計結果就可以判斷中位數落到那個區域，同時知道這個區域中的第幾大數剛好是中位數。然後第二次掃描我們只統計落在這個區域中的那些數就可以了。
   實際上，如果不是int是int64，我們可以經過3次這樣的劃分即可降低到可以接受的程度。即可以先將int64分成2^24個區域，然後確定區域的第幾大數，在將該區域分成2^20個子區域，然後確定是子區域的第幾大數，然後子區域裡的數的個數只有2^20，就可以直接利用direct addr table進行統計了。
2. 　　思路二@綠色夾克衫：同樣需要做兩遍統計，如果資料存在硬碟上，就需要讀取2次。
   方法同基數排序有些像，開一個大小為65536的Int陣列，第一遍讀取，統計Int32的高16位的情況，也就是0-65535，都算作0,65536 - 131071都算作1。就相當於用該數除以65536。Int32 除以 65536的結果不會超過65536種情況，因此開一個長度為65536的陣列計數就可以。每讀取一個數，陣列中對應的計數+1，考慮有負數的情況，需要將結果加32768後，記錄在相應的陣列內。
   第一遍統計之後，遍歷陣列，逐個累加統計，看中位數處於哪個區間，比如處於區間k，那麼0- k-1的區間裡數字的數量sum應該<n/2（2.5億）。而k+1 - 65535的計數和也<n/2，第二遍統計同上面的方法類似，但這次只統計處於區間k的情況，也就是說(x / 65536) + 32768 = k。統計只統計低16位的情況。並且利用剛才統計的sum，比如sum = 2.49億，那麼現在就是要在低16位裡面找100萬個數(2.5億-2.49億)。這次計數之後，再統計一下，看中位數所處的區間，最後將高位和低位組合一下就是結果了。

密匙三：Bloom filter/Bitmap

Bloom filter

關於什麼是Bloom filter，請參看blog內此文：

• 海量資料處理之Bloom Filter詳解

　　適用範圍：可以用來實現資料字典，進行資料的判重，或者集合求交集
　　基本原理及要點：
　　對於原理來說很簡單，位陣列+k個獨立hash函式。將hash函式對應的值的位陣列置1，查詢時如果發現所有hash函式對應位都是1說明存在，很明顯這個過程並不保證查詢的結果是100%正確的。同時也不支援刪除一個已經插入的關鍵字，因為該關鍵字對應的位會牽動到其他的關鍵字。所以一個簡單的改進就是 counting Bloom filter，用一個counter陣列代替位陣列，就可以支援刪除了。
　　還有一個比較重要的問題，如何根據輸入元素個數n，確定位陣列m的大小及hash函式個數。當hash函式個數k=(ln2)*(m/n)時錯誤率最小。在錯誤率不大於E的情況下，m至少要等於n*lg(1/E)才能表示任意n個元素的集合。但m還應該更大些，因為還要保證bit陣列裡至少一半為0，則m應該>=nlg(1/E)*lge 大概就是nlg(1/E)1.44倍(lg表示以2為底的對數)。
　　舉個例子我們假設錯誤率為0.01，則此時m應大概是n的13倍。這樣k大概是8個。
　　注意這裡m與n的單位不同，m是bit為單位，而n則是以元素個數為單位(準確的說是不同元素的個數)。通常單個元素的長度都是有很多bit的。所以使用bloom filter記憶體上通常都是節省的。

　　擴充套件：

　　Bloom filter將集合中的元素對映到位陣列中，用k（k為雜湊函式個數）個對映位是否全1表示元素在不在這個集合中。Counting bloom filter（CBF）將位陣列中的每一位擴充套件為一個counter，從而支援了元素的刪除操作。Spectral Bloom Filter（SBF）將其與集合元素的出現次數關聯。SBF採用counter中的最小值來近似表示元素的出現頻率。

   可以看下上文中的第6題：

“6、給你A,B兩個檔案，各存放50億條URL，每條URL佔用64位元組，記憶體限制是4G，讓你找出A,B檔案共同的URL。如果是三個乃至n個檔案呢？

　　根據這個問題我們來計算下記憶體的佔用，4G=2^32大概是40億*8大概是340億，n=50億，如果按出錯率0.01算需要的大概是650億個bit。現在可用的是340億，相差並不多，這樣可能會使出錯率上升些。另外如果這些urlip是一一對應的，就可以轉換成ip，則大大簡單了。

    同時，上文的第5題：給定a、b兩個檔案，各存放50億個url，每個url各佔64位元組，記憶體限制是4G，讓你找出a、b檔案共同的url？如果允許有一定的錯誤率，可以使用Bloom filter，4G記憶體大概可以表示340億bit。將其中一個檔案中的url使用Bloom filter對映為這340億bit，然後挨個讀取另外一個檔案的url，檢查是否與Bloom filter，如果是，那麼該url應該是共同的url（注意會有一定的錯誤率）。”

Bitmap

• 關於什麼是Bitmap，請看blog內此文第二部分：http://blog.csdn.net/v_july_v/article/details/6685962。

    下面關於Bitmap的應用，可以看下上文中的第13題，以及另外一道新題：

“13、在2.5億個整數中找出不重複的整數，注，記憶體不足以容納這2.5億個整數。

    方案1：採用2-Bitmap（每個數分配2bit，00表示不存在，01表示出現一次，10表示多次，11無意義）進行，共需記憶體2^32 * 2 bit=1 GB記憶體，還可以接受。然後掃描這2.5億個整數，檢視Bitmap中相對應位，如果是00變01，01變10，10保持不變。所描完事後，檢視bitmap，把對應位是01的整數輸出即可。
    方案2：也可採用與第1題類似的方法，進行劃分小檔案的方法。然後在小檔案中找出不重複的整數，並排序。然後再進行歸併，注意去除重複的元素。”

15、給40億個不重複的unsigned int的整數，沒排過序的，然後再給一個數，如何快速判斷這個數是否在那40億個數當中？
    方案1：frome oo，用點陣圖/Bitmap的方法，申請512M的記憶體，一個bit位代表一個unsigned int值。讀入40億個數，設定相應的bit位，讀入要查詢的數，檢視相應bit位是否為1，為1表示存在，為0表示不存在。

密匙四、Trie樹/資料庫/倒排索引

Trie樹

　　適用範圍：資料量大，重複多，但是資料種類小可以放入記憶體
　　基本原理及要點：實現方式，節點孩子的表示方式
　　擴充套件：壓縮實現。
　　問題例項：

1. 上面的第2題：尋找熱門查詢：查詢串的重複度比較高，雖然總數是1千萬，但如果除去重複後，不超過3百萬個，每個不超過255位元組。
   
2. 上面的第5題：有10個檔案，每個檔案1G，每個檔案的每一行都存放的是使用者的query，每個檔案的query都可能重複。要你按照query的頻度排序。
3. 1000萬字串，其中有些是相同的(重複),需要把重複的全部去掉，保留沒有重複的字串。請問怎麼設計和實現？
4. 上面的第8題：一個文字檔案，大約有一萬行，每行一個詞，要求統計出其中最頻繁出現的前10個詞。其解決方法是：用trie樹統計每個詞出現的次數，時間複雜度是O(n*le)（le表示單詞的平準長度），然後是找出出現最頻繁的前10個詞。

    更多有關Trie樹的介紹，請參見此文：從Trie樹（字典樹）談到字尾樹。

資料庫索引
　　適用範圍：大資料量的增刪改查
　　基本原理及要點：利用資料的設計實現方法，對海量資料的增刪改查進行處理。

• 關於資料庫索引及其優化，更多可參見此文：http://www.cnblogs.com/pkuoliver/archive/2011/08/17/mass-data-topic-7-index-and-optimize.html；
• 關於MySQL索引背後的資料結構及演算法原理，這裡還有一篇很好的文章：http://blog.codinglabs.org/articles/theory-of-mysql-index.html；
• 關於B 樹、B+ 樹、B* 樹及R 樹，本blog內有篇絕佳文章：http://blog.csdn.net/v_JULY_v/article/details/6530142。

倒排索引(Inverted index)
　　適用範圍：搜尋引擎，關鍵字查詢
　　基本原理及要點：為何叫倒排索引？一種索引方法，被用來儲存在全文搜尋下某個單詞在一個文件或者一組文件中的儲存位置的對映。
　以英文為例，下面是要被索引的文字：
    T0 = "it is what it is"
    T1 = "what is it"
    T2 = "it is a banana"
    我們就能得到下面的反向檔案索引：
    "a":      {2}
    "banana": {2}
    "is":     {0, 1, 2}
    "it":     {0, 1, 2}
    "what":   {0, 1}
　檢索的條件"what","is"和"it"將對應集合的交集。

　　正向索引開發出來用來儲存每個文件的單詞的列表。正向索引的查詢往往滿足每個文件有序頻繁的全文查詢和每個單詞在校驗文件中的驗證這樣的查詢。在正向索引中，文件佔據了中心的位置，每個文件指向了一個它所包含的索引項的序列。也就是說文件指向了它包含的那些單詞，而反向索引則是單詞指向了包含它的文件，很容易看到這個反向的關係。
　　擴充套件：
　　問題例項：文件檢索系統，查詢那些檔案包含了某單詞，比如常見的學術論文的關鍵字搜尋。

    關於倒排索引的應用，更多請參見：

• 第二十三、四章：楊氏矩陣查詢，倒排索引關鍵詞Hash不重複編碼實踐，
• 第二十六章：基於給定的文件生成倒排索引的編碼與實踐。

密匙五、外排序

　　適用範圍：大資料的排序，去重
　　基本原理及要點：外排序的歸併方法，置換選擇敗者樹原理，最優歸併樹
　　擴充套件：
　　問題例項：
　　1).有一個1G大小的一個檔案，裡面每一行是一個詞，詞的大小不超過16個位元組，記憶體限制大小是1M。返回頻數最高的100個詞。
　　這個資料具有很明顯的特點，詞的大小為16個位元組，但是記憶體只有1M做hash明顯不夠，所以可以用來排序。記憶體可以當輸入緩衝區使用。

    關於多路歸併演算法及外排序的具體應用場景，請參見blog內此文：

• 第十章、如何給10^7個資料量的磁碟檔案排序

密匙六、分散式處理之Mapreduce

    MapReduce是一種計算模型，簡單的說就是將大批量的工作（資料）分解（MAP）執行，然後再將結果合併成最終結果（REDUCE）。這樣做的好處是可以在任務被分解後，可以通過大量機器進行平行計算，減少整個操作的時間。但如果你要我再通俗點介紹，那麼，說白了，Mapreduce的原理就是一個歸併排序。

        適用範圍：資料量大，但是資料種類小可以放入記憶體
　　基本原理及要點：將資料交給不同的機器去處理，資料劃分，結果歸約。
　　擴充套件：
　　問題例項：

1. The canonical example application of MapReduce is a process to count the appearances of each different word in a set of documents:
2. 海量資料分佈在100臺電腦中，想個辦法高效統計出這批資料的TOP10。
3. 一共有N個機器，每個機器上有N個數。每個機器最多存O(N)個數並對它們操作。如何找到N^2個數的中數(median)？

    更多具體闡述請參見blog內：

• 從Hadhoop框架與MapReduce模式中談海量資料處理，
• 及MapReduce技術的初步瞭解與學習。

其它模式/方法論，結合作業系統知識

    作業系統中的方法，先生成4G的地址表，在把這個表劃分為小的4M的小檔案做個索引，二級索引。30位前十位表示第幾個4M檔案，後20位表示在這個4M檔案的第幾個，等等，基於key value來設計儲存，用key來建索引。

    但如果現在只有10000個數，然後怎麼去隨機從這一萬個數裡面隨機取100個數？請讀者思考。更多海里資料處理面試題，請參見此文第一部分：http://blog.csdn.net/v_july_v/article/details/6685962。

參考文獻

1. 十道海量資料處理面試題與十個方法大總結；
2. 海量資料處理面試題集錦與Bit-map詳解；
3. 十一、從頭到尾徹底解析Hash表演算法；
4. 海量資料處理之Bloom Filter詳解；
5. 從Trie樹（字典樹）談到字尾樹；
6. 第三章續、Top K演算法問題的實現；
7. 第十章、如何給10^7個資料量的磁碟檔案排序；
8. 從B樹、B+樹、B*樹談到R 樹；
9. 第二十三、四章：楊氏矩陣查詢，倒排索引關鍵詞Hash不重複編碼實踐；
10. 第二十六章：基於給定的文件生成倒排索引的編碼與實踐；
11. 從Hadhoop框架與MapReduce模式中談海量資料處理；
12. 第十六~第二十章：全排列，跳臺階，奇偶排序，第一個只出現一次等問題；
13. http://blog.csdn.net/v_JULY_v/article/category/774945；
14. STL原始碼剖析第五章，侯捷著；
15. 2012百度實習生招聘筆試題：http://blog.csdn.net/hackbuteer1/article/details/7542774。

後記