POJ 2352（順路講解一下樹狀陣列）

接觸到的第一道樹狀陣列的題，AC之後感覺對樹狀陣列思想的理解明顯清晰了很多，入門必備呀。

先來講講樹狀陣列吧。

上個圖

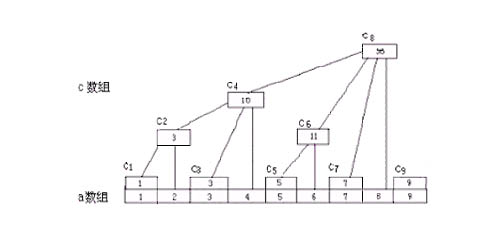
如果要求區間和，例如求a3->a8，我們先用陣列c來記錄下來各個區間的和，那麼就可以直接c8-c2就可以得到a3->a8的區間和了。

c[n]陣列的下標是用來記錄陣列a[1]->a[n]的區間和。

再想，我們如果要求s->t的和可以怎麼求？

是不是可以用(1->t)減去(1->s-1)？

同理，樹狀陣列也可以用這種方式求和。比如求a[2]的話就可以用c[2]-c[1]來得到a[2]。

關於c陣列的記錄方法，就不得不提到x&(-x)這個表示式。

x&(-x)是用來計算每次查詢或者更新時候c陣列的偏移量。

通常寫成函式的形式。

int lowbit(int x)
{
    return x & (-x);
}

注意：計算機中負數是用的補碼錶示的，正數是用的原碼錶示，可以自己拿張草稿紙來實現一下x&(-x)的計算

關於樹狀陣列的求區間和，如果求區間[1,8]，那麼直接c[8]就好，但是如果要求區間[4,8]該怎麼辦？

那麼可以用區間[1,8]的和減去區間[1,3]的和就得到了區間[4,8]的和。

那又如何求區間[1,3]呢？我們可以c[2]+c[3]就得到了區間[1,3]的和了。

下面是求區間[1,x]和的函式：

int sum(int x)
{
    int s = 0;
    while (x > 0)
    {
        s += c[x];
        x -= lowbit(x);
    }
    return s;
}

以求區間[1,3]為例，首先x等於3代入方程，3 > 0，則s = c[3]，然後執行x-=lowbit(x);

讓我們進入lowbit函式，首先3的二進位制原碼為0000 0011，-3為3的補碼，則-3的二進位制碼為1111 1101，進行&運算之後為1，所以x-=1，此時x為2。由於2>0，所以s此時等於c[3] + c[2]。執行x-=lowbit(x)之後x = 0。迴圈結束，此時s已經是區間[1,3]的和了。

我們再來看樹狀陣列的更新函式：

int update(int x， int num)
{
    while (x <= MAX)
    {
        c[x] += num;
        x += lowbit(x);
    }
}

和線段樹一樣，樹狀陣列也是需要對節點所影響到的所有節點進行更新，採取從根到頂的方式。也就是對每個影響到的節點都加上更改資訊。

樹狀陣列時間複雜度O(log n)

————————————————————————分割線——————————————————————————————

題意：有n個星星節點，存在星星節點左下角（包括正左和正下）的其他星星節點，則該星星節點比它左下角的星星節點大，level 0表示該星星節點沒有比他還小的節點，level 1表示存在一個比該星星節點小的點。輸出統計好的每個level等級存在多少星星節點。

解題思路：為什麼要用樹狀陣列呢，因為如果你用for迴圈統計的話，由於資料很大然後又有很多組資料需要統計，那麼肯定是會超時的，所以此時需要一種高效的資料結構（感覺像一句廢話TAT），樹狀陣列類似於線段樹，能夠很高效的解決區間問題，將這道題提煉一下其實也就是一個統計區間和的問題，線段樹寫起來好麻煩的=。=於是乎用了樹狀陣列。

直接上程式碼：

/*因為是按照y升序輸入，所以後面輸入對前面輸入並無影響
**前x與後x如果相同，那麼肯定後x是包含前x的，因為是按照y升序
**即前後x雖是在同一列，但後x肯定在前x上面，即包含前x
**PS:樹狀陣列下標從1開始
*/
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int level[32001];
int c[32001];
int lowbit(int x)
{
    return x & (-x);
}
int sum(int x)
{
    int s = 0;
    while (x > 0)
    {
        s += c[x];
        x -= lowbit(x);
    }
    return s;
}
int update(int x)
{
    while (x <= 32001)
    {
        c[x]++;
        x += lowbit(x);
    }
}
int main()
{
    int n;
    int x, y;
    while(~scanf("%d", &n))
    {
        int N = n;
        memset(level, 0, sizeof(level));
        memset(c, 0, sizeof(c));
        while (n--)
        {
            scanf("%d %d", &x, &y);
            level[sum(x+1)]++;
            update(x+1);
        }
        for (int i = 0; i <= N - 1; i++)
            printf("%d\n", level[i]);
    }
    return 0;
}