裁剪演算法 - Cohen Sutherland Clipping的原理及Java實現

jinbing_peng發表於2015-04-01
演算法Java

裁剪是3D圖形的一個非常重要的方面，二維裁剪功能被廣泛的應用於三維影象領域。本文結合Java程式碼例項，介紹一個非常好，但又足夠簡單的裁剪演算法-科恩-薩瑟蘭演算法.

在繪製2D線段時，線段的一個端點或者兩個端點可能位於螢幕外面，而其中的一部分仍然是可見的。在這種情況下，需要一個有效的演算法來查詢可見部分的兩個新端點，只繪製基於新端點的線段，所有在螢幕外的部分被裁剪掉，從而提高程式的效率。

演算法

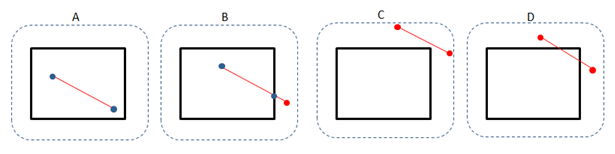
繪製線段時，如果線段的一個端點是螢幕外，另一個在裡面，通過裁剪，只保留螢幕內部的部分。即使兩個端點都在畫面外，該線段的一部分也可能是可見的。裁剪演算法需要找到可見部分線段的新端點，新端點位於螢幕內部或螢幕的邊緣。如下圖，黑色矩形表示螢幕，紅色是原始線段的端點，藍色為裁剪後線段的端點：

這裡寫圖片描述

  • A：兩個端點都在螢幕上，無需裁剪。
  • B：一個端點在螢幕外，一個端點在螢幕內部，螢幕外的端點需要被裁剪。
  • C：兩個端點都在螢幕外面，該線段的任何部分都不可見，無需裁剪
  • D：兩個端點是畫面外，但線段的一部分是可見的，兩個端點都需要被裁剪。

如果繼續細分，還有很多不同的情況，比如，每個端點可以在螢幕內部，左邊，右邊，上面，下面，等… 本演算法可以非常有效地識別這些情況，並作對應的裁剪。

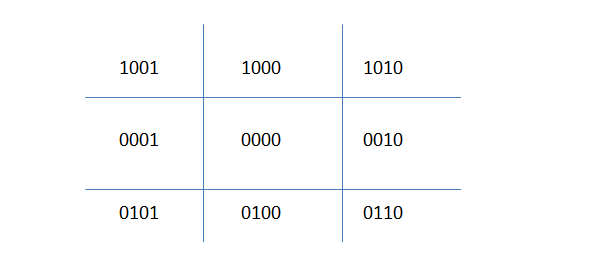
該演算法將2D空間分為9個區域：中心區域是在螢幕，其它的8個區域是在螢幕以外的不同側面。每個區域用一個四位的二進位制數來標識，該二進位制數標識被稱為區域碼（“outcode”）。編碼如下：

這裡寫圖片描述

  • 如果該區域在螢幕的上方，第一個位元組位是1
  • 如果該區域在螢幕的下方，第二個位元組位是1
  • 如果該區域在螢幕的右邊，第三個位元組位是1
  • 如果該區域在螢幕的左側，第四個位元組位為1

顯然，同一區域不能同時在左和右邊，或同時在上方和下方，所以在第三位元組位和第四位元組位不能為同時為1，第一位元組位和第二位元組位的不能同時為1。螢幕區域的4個位元組位全部為0。

螢幕區域的Java定義如下，

private static final int INSIDE = 0;
private static final int LEFT = 1;
private static final int RIGHT = 2;
private static final int BOTTOM = 4;
private static final int TOP = 8;

線段的兩個端點可以位於任意9個區域，我們先從一些簡單的情形入手：

  • 如果兩個端點均在螢幕的內部或邊緣，該線段不需要裁剪並需要全部繪製。這種情況下，是簡單接受（Trivial Accept）。
  • 如果兩個端點均在螢幕（例如，兩個端點都在螢幕上方）的同一側，線段的任何部分都不在螢幕上，該線段不需要裁剪並不需繪製，這種情況下，是簡單拒絕（Trivial Reject）。

以上兩種情況下可以很容易地通過各區域的區域碼(outcode)識別出來：

  • Trivial Accept：兩個端點必須位於程式碼0000的區域中，所以Trivial Accept的情況可以通過 code1 | code2 == 0 來斷定。(其中，code1 和code2 的線段兩個端點的程式碼，’|’ 是二進位制OR運算子，如果code1 和code2都是0，則code1 | code2 == 0)。
  • Trivial Reject：兩個端點均在區域的同一側，這兩個碼有兩個相應的位元組位都是1。例如，如果只有兩個端點是在螢幕的左側，兩個程式碼的第四位均為1。因此，Trivial Reject的情況可以通過code1 & code2 != 0來斷定。

其它情況（既不是Trivial Accept，也不是Trivial Reject），通過裁剪操作，可以轉化成如上的簡單的情況。科恩薩瑟蘭演算法是一種迴圈，每個迴圈只做一個裁剪操作。該操作裁剪其中一個端點，直到新的端點位於螢幕的水平或者垂直邊界。在許多情況下，需要多次裁剪才能夠最終斷定是否該線段被接受或拒絕。但裁剪的次數最多為4次。

螢幕可通過兩個坐上方的點P1（xMin,yMin）,右下方的點P2(xMax, yMax) 來定義, Java 定義如下

    private double xMin;
    private double yMin;
    private double xMax;
    private double yMax;

Clip method用到了一個輔助功能，getRegionCode，該method返回給定端點的二進位制區域程式碼

    private final int getRegionCode(double x, double y) {
        int xcode = x < xMin ? LEFT : x > xMax ? RIGHT : INSIDE;
        int ycode = y < yMin ? BOTTOM : y > yMax ? TOP : INSIDE;
        return xcode | ycode;
    }

Clip功能開始檢測簡單的情形：

    public boolean clip(Line2D.Float line) {
        double p1x = line.getX1(), p1y = line.getY1();
        double p2x = line.getX2(), p2y = line.getY2();
        double qx = 0d, qy = 0d;
        boolean vertical = p1x == p2x;
        double slope = vertical ? 0d : (p2y - p1y) / (p2x - p1x);

        int c1 = getRegionCode(p1x, p1y);
        int c2 = getRegionCode(p2x, p2y);

        while (true) {
            if(c1 == INSIDE & c2 == INSIDE){
                break;
            }

            if ((c1 & c2) != INSIDE){
                return false;
            }

如果c1 == INSIDE & c2 == INSIDE 為true, 即為簡單接受（Trivial Accept），通過break 跳轉到結束程式碼.

        line.setLine(p1x, p1y, p2x, p2y);
        return true;

如果 (c1 & c2) != INSIDE為true, 即為簡單拒絕（Trivial Reject）。直接返回false;

如果沒有檢測到簡單的情形，該線段需要被裁剪。每個迴圈只作4個可能的剪裁操作其中的一個。剪輯，一個座標的一個端點被設定為原線段與對應區域的邊界的交點，新的端點是在螢幕的邊界座標之一，該點的其它座標值是由直線的方程重新計算。為了找到對應的裁剪操作，我們需要找到螢幕的外部的端點。該端點的程式碼稱為codeout，選擇code1或code2中不等於0的一個。

            int c = code1 == INSIDE ? code2 : code1;

            if ((c & LEFT) != INSIDE) {
                qx = xMin;
                qy = (qx - p1x) * slope + p1y;
            } else if ((c & RIGHT) != INSIDE) {
                qx = xMax;
                qy = (qx - p1x) * slope + p1y;
            } else if ((c & BOTTOM) != INSIDE) {
                qy = yMin;
                qx = vertical ? p1x : (qy - p1y) / slope + p1x;
            } else if ((c & TOP) != INSIDE) {
                qy = yMax;
                qx = vertical ? p1x : (qy - p1y) / slope + p1x;
            }

上述程式碼計算裁剪之後新的端點座標，新的座標必須賦給端點p1或端點p2的, p1 和 p2 的選取取決於哪個codeout的值。迴圈結束之後，新線段可能滿足一個簡單的情況下，如果仍然不滿足一個簡單的情況，則進行新的迴圈並作裁剪操作。

            if (c == code1) {
                p1x = qx;
                p1y = qy;
                code1 = getRegionCode(p1x, p1y);
            } else {
                p2x = qx;
                p2y = qy;
                code2 = getRegionCode(p2x, p2y);
            }

最後附上完整的程式碼實現

    public final class Clipping {
        private static final int INSIDE = 0;
        private static final int LEFT = 1;
        private static final int RIGHT = 2;
        private static final int BOTTOM = 4;
        private static final int TOP = 8;

        private double xMin;
        private double yMin;
        private double xMax;
        private double yMax;

        public Clipping() {
        }

        public Clipping(Rectangle2D clip) {
            setClip(clip);
        }

        public void setClip(Rectangle2D clip) {
            xMin = clip.getX();
            xMax = xMin + clip.getWidth();
            yMin = clip.getY();
            yMax = yMin + clip.getHeight();
        }

        private final int getRegionCode(double x, double y) {
            int xcode = x < xMin ? LEFT : x > xMax ? RIGHT : INSIDE;
            int ycode = y < yMin ? BOTTOM : y > yMax ? TOP : INSIDE;
            return xcode | ycode;
        }

        public boolean clip(Line2D.Float line) {
            double p1x = line.getX1(), p1y = line.getY1();
            double p2x = line.getX2(), p2y = line.getY2();
            double qx = 0d, qy = 0d;
            boolean vertical = p1x == p2x;
            double slope = vertical ? 0d : (p2y - p1y) / (p2x - p1x);

            int code1 = getRegionCode(p1x, p1y);
            int code2 = getRegionCode(p2x, p2y);

            while (true) {
                if(code1 == INSIDE & code2 == INSIDE){
                    break;
                }           

                if ((code1 & code2) != INSIDE){
                    return false;
                }

                int codeout = code1 == INSIDE ? code2 : code1;

                if ((codeout & LEFT) != INSIDE) {
                    qx = xMin;
                    qy = (qx - p1x) * slope + p1y;
                } else if ((codeout & RIGHT) != INSIDE) {
                    qx = xMax;
                    qy = (qx - p1x) * slope + p1y;
                } else if ((codeout & BOTTOM) != INSIDE) {
                    qy = yMin;
                    qx = vertical ? p1x : (qy - p1y) / slope + p1x;
                } else if ((codeout & TOP) != INSIDE) {
                    qy = yMax;
                    qx = vertical ? p1x : (qy - p1y) / slope + p1x;
                }

                if (codeout == code1) {
                    p1x = qx;
                    p1y = qy;
                    code1 = getRegionCode(p1x, p1y);
                } else {
                    p2x = qx;
                    p2y = qy;
                    code2 = getRegionCode(p2x, p2y);
                }
            }
            line.setLine(p1x, p1y, p2x, p2y);
            return true;
        }
    }

本文主要參考自http://lodev.org/cgtutor/lineclipping.html， 並結合實際的遊戲引擎，給出了Java版本的程式碼實現。希望對你有所幫助！ 反饋請聯絡jinbing.peng@yahoo.com.

相關文章