很詭異的博弈問題分析方法

    小學奧賽的經典題目：兩個人輪流在黑板上寫一個不大於10的正整數。規定不準把已經寫過的數的約數再寫出來。誰最後沒寫的了誰就輸了。問是先寫的人必勝還是後寫的人必勝，必勝策略是什麼。
    答案很巧妙。先寫者有必勝策略。他可以先寫下數字6，現在就只剩下4、5、7、8、9、10可以寫了。把剩下的6個數分成三對，分別是(4,5)、(7,9)、(8,10)，每一對裡的兩個數都不成倍數關係，且它們各自的倍數（如果出現過）必然是同時出現。因此不管你寫什麼數，我就寫它所在的數對裡的另一個數，這樣可以保證我總有寫的。
    今天偶然看到一個加強版，不知大家見過沒有：規則不變，可以寫的數擴充套件到所有不大於n的正整數。對於哪些n先寫者必勝？證明你的結論。
































    你會有一種被騙的感覺-_-b
    其實，不管n是多少，先寫者總有必勝策略。考慮一個新的規則“不準寫數字1”。如果加上這個新規則後先寫者有必勝策略，那麼這個策略對於原遊戲同樣適用（因為1是所有數的約數，本來就不能寫）；如果在新規則下後寫者必勝，則原遊戲中的先寫者寫下數字1，然後他就變成了新規則下的後寫者。於是不管怎麼樣，先寫者總是有必勝策略。
    To 3樓：忘了提一句，只要是雙方共用狀態（合法的決策完全相同）的對弈遊戲，其中一方肯定有必勝策略。棋局的任一狀態只有兩種，面對這個棋局的人要麼必勝要麼必敗。考慮這樣的一個遞推關係：如果一個狀態是必勝態，那至少有一種走法能走成一個必敗態留給對方；如果一個狀態是必敗態，那它怎麼走都只能走到必勝態。運用這樣的關係，我們可以自底向上推出初始狀態是必勝還是必敗。

    
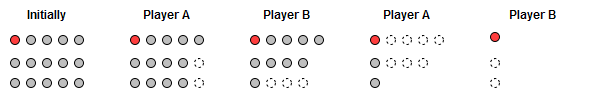
    Update: 感謝網友FreePeter的精彩評論。這種分析方法有一種很形象的名字叫做Strategy-stealing，它的另一個經典例子是Chomp遊戲。遊戲在一塊矩形的巧克力上進行，巧克力被分為MxN塊。兩人輪流選擇其中一個格子，然後吃掉這一格及它右邊、下邊和右下角的所有格子。最左上角的那一塊巧克力有毒，誰吃到誰就輸了。上圖是一個可能的對戰過程。我們可以用類似的方法證明先手必勝。假設後手有必勝策略，那麼先手把最右下角的那一塊取走。注意到接下來對方不管走哪一步，最右下角的那一塊本來也會被取走，因此整個棋局並無變化，只是現在的先手扮演了後手的角色，可以用後手的那個必勝策略來應對棋局，這樣便巧妙地“偷”走了後手的必勝策略。
    上面所舉的例子都是雙方共用狀態的遊戲（ICG遊戲），因此至少有一方存在必勝策略。對於其它一些非ICG遊戲，我們也可以用類似的方法證明後手不可能有必勝策略（但在這裡並不能說明先手一定必勝）。比如對於井字棋遊戲，假設後手有必勝策略，那先手就隨便走一步，以後就裝成是後手來應對。如果在哪一步需要先手在已經下過子的地方落子，他就再隨便走一步就是了。這種證明方法成立的前提就是，多走一步肯定不是壞事。事實上，對於所有這種“多走一步肯定不是壞事”的且決策對稱的遊戲，我們都可以證明後手是沒有必勝策略的。