【分治演算法】歸併排序，快速排序和漢諾塔

1介紹

分治演算法已經是本人所寫的常用演算法系列的第三個了，可能只會寫這一節，對比動態規劃與貪心演算法我們來認識一下分治演算法。
從思路上來看：
（1）動態規劃：多階段過程轉化為一系列單階段問題，利用各階段之間的關係，逐個求解。每一個階段的最優解是基於前一個階段的最優解。
（2）貪心演算法：選擇的貪心策略必須具備無後效性，即某個狀態以前的過程不會影響以後的狀態，只與當前狀態有關。不是對所有問題都能得到整體最優解。
（3）分治演算法：將一個大規模的問題分解成n個容易解決的小問題，當小問題被解決時，最終的問題也被解決了。
乍一看，似乎區別不大。
從程式碼結構上來看（不絕對）：
（1） 動態規劃：通常為兩層for迴圈巢狀；
（2） 貪心演算法：通常先進行排序，後進行選擇；
（3） 分治演算法：通常為遞迴；

2歸併排序

2.1問題

問題：使用歸併排序以下數字：8，7，4，2，2，1，19，23，5，3

2.2解析

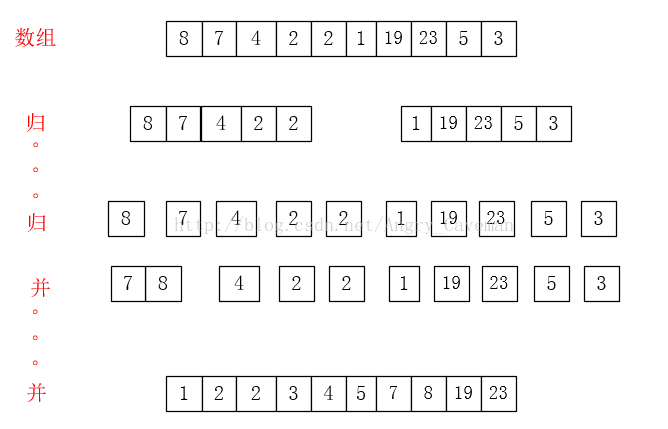
按照分治演算法的思想，題中陣列Array有10個數字，不太方便操作，應該將其分解為若干個容易解決的子問題。假設現在排序的是包含1個數字的陣列Array，是不是就非常容易了（一個數字都不用排序）。
現將陣列Array分解為10個陣列，每個陣列只含有1個數字，這就是歸併排序中“歸”的過程。

陣列只含有1個數字，可見該陣列已經有序了。然後將兩個有序的陣列合並起來，當然合併的時候也要確保合併之後的陣列也是有序的。這就是歸併排序中“並”的過程。

歸併排序的處理過程：
（1）“歸”：拆分為只含有一個數字的陣列；

void SplitSort(int first,int last,int a[],int temp[]){
	if (last>first){
		int mid = (first + last) / 2;
		SplitSort(first,mid,a,temp);
		SplitSort(mid+1,last,a,temp);
		MergeSort(first,last,mid,a,temp);
	}
}

（2）“並”：將兩個有序的陣列合併成一個有序的陣列；

void MergeSort(int first,int last,int mid,int a[],int temp[]){
	int i = first, j = mid + 1;
	int m = mid, n = last;
	int k = 0;

	while (i <= m && j <= n)
	{
		if (a[i] <= a[j])
			temp[k++] = a[i++];
		else
			temp[k++] = a[j++];
	}

	while (i <= m)
		temp[k++] = a[i++];

	while (j <= n)
		temp[k++] = a[j++];

	for (i = 0; i < k; i++)
		a[first + i] = temp[i];
}

本題完整原始碼：

#include<iostream>
using namespace std;
#define Max 10

//歸併排序
void MergeSort(int first,int last,int mid,int a[],int temp[]){
	int i = first, j = mid + 1;
	int m = mid, n = last;
	int k = 0;

	while (i <= m && j <= n)
	{
		if (a[i] <= a[j])
			temp[k++] = a[i++];
		else
			temp[k++] = a[j++];
	}

	while (i <= m)
		temp[k++] = a[i++];

	while (j <= n)
		temp[k++] = a[j++];

	for (i = 0; i < k; i++)
		a[first + i] = temp[i];
}
void SplitSort(int first,int last,int a[],int temp[]){
	if (last>first){
		int mid = (first + last) / 2;
		SplitSort(first,mid,a,temp);
		SplitSort(mid+1,last,a,temp);
		MergeSort(first,last,mid,a,temp);
	}
}
bool Merge(int a[],int n){
	int *temp = new int[n];
	if (temp == NULL)
		return false;
	SplitSort(0,n-1,a,temp);
	return true;
}
int main(){
	int array[Max] = { 8, 7, 4, 2, 2, 1, 19, 23, 5, 3 };
	Merge(array,Max);
	//列印
	int i;
	for (i = 0; i < Max;i++){
		cout << array[i] << " ";
	}
	return 0;
}

2.3結果

3快速排序

3.1問題

問題：使用快速排序一下數字：8，7，4，2，2，1，19，23，5，3

3.2解析

同樣按照分治演算法思想，還是要將其拆分為容易解決的子問題，不過，與歸併演算法的不同之處在於不是將其拆分為只含一個數字的陣列，畢竟容易解決地子問題不只那一個。

拋開眼前的問題，假設現在有一個陣列Array[3]={3,1,2}，如果我們要對其排序的話，可以得到Array[1]==1，可見，只有讓在陣列中大於Array[1]的數字位於其右邊（Array[1]）, 小於Array[1]的數字位於其左邊（Array[0]），那麼Array也就有序了。

基於以上推導，這個容易解決的子問題就是，讓大於某個數的數字位於其右邊，小於該數字則位於其左邊，這個數在快速排序中稱為基數。當然還有很多困惑的地方，比如，基數左右兩邊的陣列仍然是亂序的，結合下圖來看看詳細的快速排序過程。

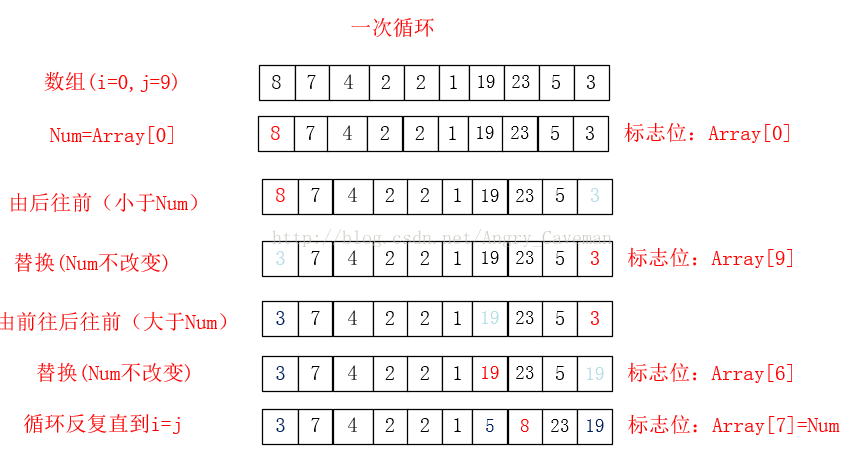
快速排序：

（1）      從陣列Array[n]中任意選取一個數作為基數num，預設num=Array[0];並將此處設為標誌位。

（2）      在Array[n]中，從後往前找小於num的數字，若Array[m1]<num，則將此數字放置在標誌位（0）上，並將m1設為標誌位。

（3）      隨後，由之前的標誌位往（0）後找，若Array[m2]>num, 則將此數字放置在標誌位m1上，並將m2設為標誌位。

（4）      如圖直到i=j，一次迴圈結束。此時左右的兩邊的陣列仍然是亂序的，我們把左右兩邊的陣列分別看成獨立的陣列，讓其也進行同樣的迴圈，最終得到結果。

本題完整原始碼：

#include<iostream>
using namespace std;
#define Max 10

int Sort(int a[], int pos, int last){
	int i, j;
	int num;//比較項
	j = last;
	i = pos;
	num = a[i];//預設取第一個為基數
	while (i < j){
		while (i < j&&a[j] >=num)
			j--;
		if (i < j){
			a[i] = a[j];
			i++;
		}
		while (i < j&&num > a[i])
			i++;
		if (i < j){
			a[j] = a[i];
			j--;
		}
	}
	a[i] = num;
	return i;
}
void QuickSort(int a[],int pos,int n){
	if (pos < n){
		int i = Sort(a, pos, n);
		QuickSort(a, pos, i - 1);
		QuickSort(a, i + 1, n);
	}
}
int main(){
	int array[Max] = { 8,7,4,2,2,1,19,23,5,3 };
	QuickSort(array,0,Max-1);
	//列印
	int i;
	for (i = 0; i < Max; i++){
		cout << array[i] << " ";
	}
	return 0;
}

3.3結果

4漢諾塔

4.1問題

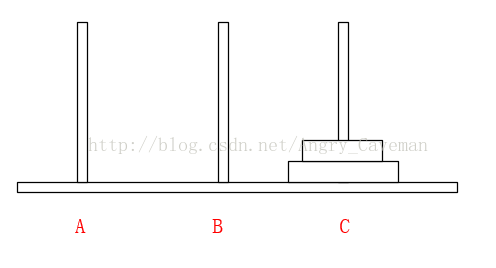
漢諾塔（Hanoi Tower），又稱河內塔，源於印度一個古老傳說。大梵天創造世界的時候做了三根金剛石柱子，在一根柱子上從下往上按照大小順序摞著64片黃金圓盤。大梵天命令婆羅門把圓盤從下面開始按大小順序重新擺放在另一根柱子上。並且規定，任何時候，在小圓盤上都不能放大圓盤，且在三根柱子之間一次只能移動一個圓盤。問應該如何操作？

4.2解析

首先要說明的一點是，以目前個人電腦的執行速度，基本上得不到64片黃金盤的結果。所以此處使用n片，n為隨意輸入的數字。

另外，題目有兩個條件：（1）小圓盤上都不能放大圓盤；（2）一次只能移動一片。

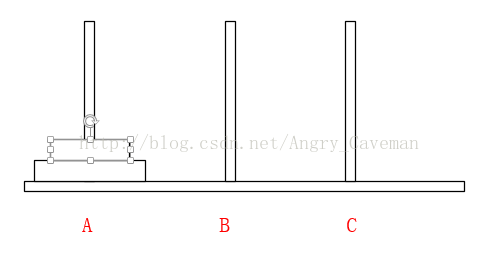
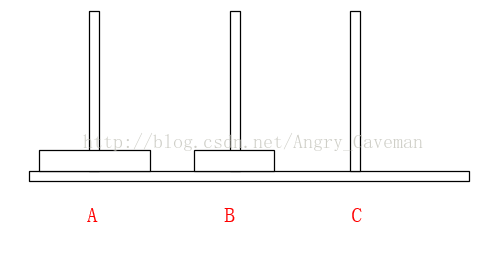
如果只有2片，由A柱移動到C柱需要進行三次操作

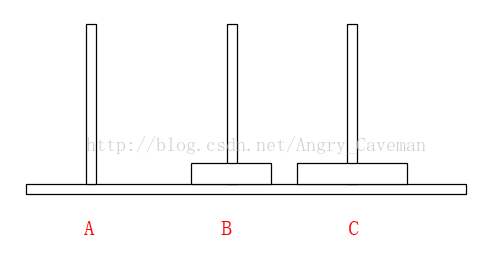
如果有3片的話，我們再來看看。

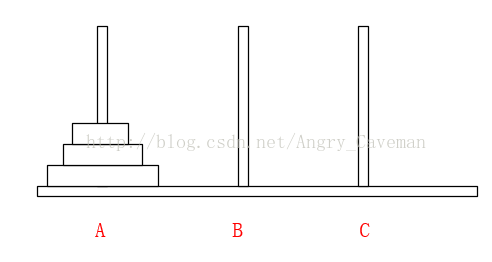
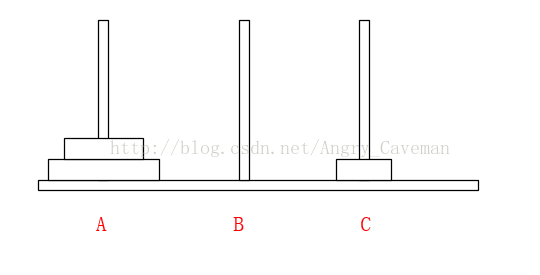
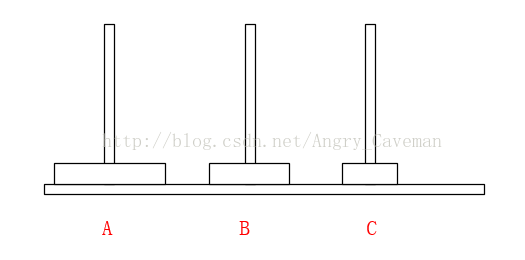
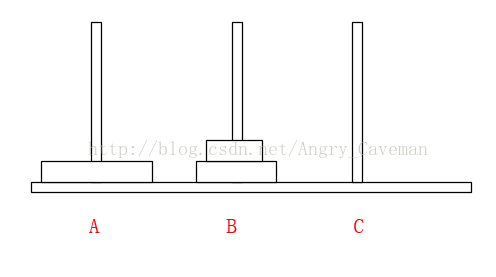
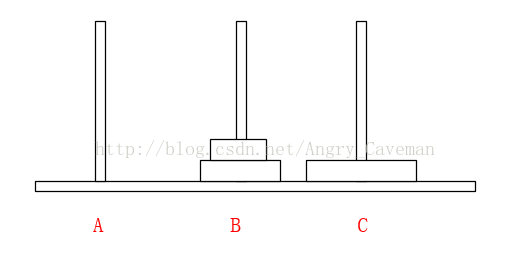
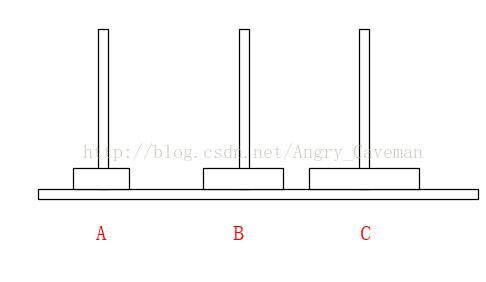
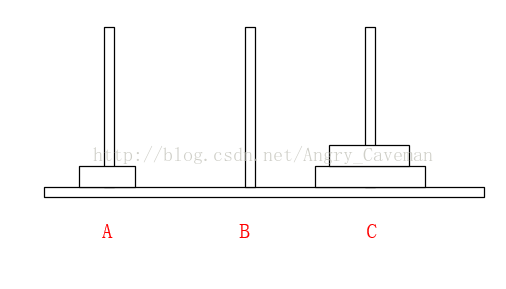
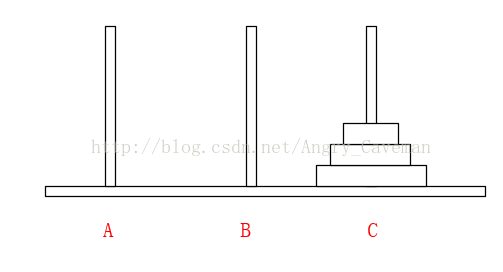
一共需要7步，總結過程：

（1）      前3步一樣，最頂層2個由A柱移動到了B柱；

（2）      最大的盤由A柱移動到C柱；

（3）      又是3步一樣的移動，最頂層2個由B柱移動到了C柱；

由此可以推匯出，F（n）=2F（n-1）+1。由該式可以看出應該使用遞迴。也就是說要得到n片怎麼挪動，就應先知道n-1片怎麼挪動，以此類推直到知道2片怎麼挪動。

         可以直接這樣理解：

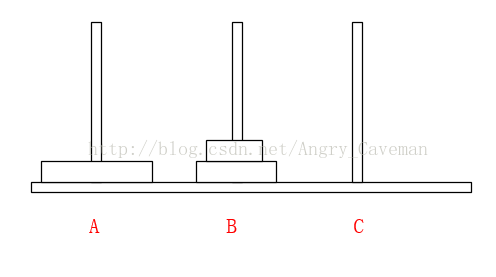
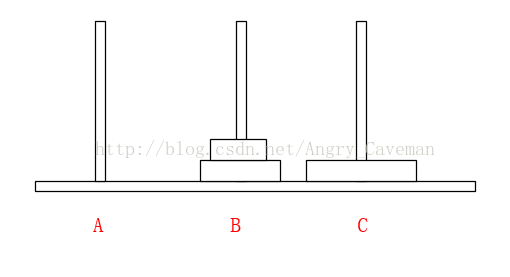
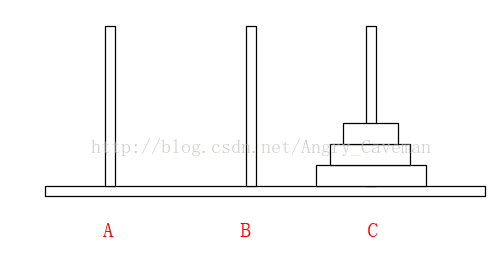
不是說一次只能移動一片嗎？因為除了最底層的盤，其上的n-1盤的移動都已經知道（遞迴），省略了具體步驟而已。

原始碼：

#include<iostream>
using namespace std;
void MoveOutput(char c1, char c2){
	cout << c1 << "-->" << c2 << endl;
}
void Hanoi(int n,char a,char b ,char c){
	if (n==1){
		MoveOutput(a, c);
		return;
	}
	Hanoi(n - 1, a,c,b);//將1到n-1片盤移動由A移動到B
	MoveOutput(a,c);//將最底層盤由A移動到C
	Hanoi(n - 1, b,a,c);//將1到n-1片盤移動由B移動到C
}

int main(){
	int num;
	cout << "輸入盤數："; cin >> num;
	Hanoi(num, 'A', 'B', 'C');
	return 0;
}

4.3結果

5總結

演算法之前就打算只寫這三類（動態規劃，貪心演算法，分治演算法），感覺用的也比較多，整個過程自己也學到不少東西，希望能共勉吧。