轉載請註明出處：http://www.cnblogs.com/WABoss/p/DP.html

 

動態規劃（Dynamic Programming, DP）是運籌學的一個分支，是求解決策過程(decision process)最優化的數學方法……

（先忘了這個吧）允許我從另一個角度去理解並解釋動態規劃，那麼開始吧。

 

一、維度

---

首先說明維度（Dimension）這個概念。這兒有一個很好很有啟發意義的回答：http://www.guokr.com/question/584012/?answer=760222#answer760222。

裡面提到所謂的維度其實就是允許某種東西自由變化的範圍。

比如說，人，人在地球上就有無數個維度，包括人當前所在的經度、緯度和高度，還有人的身高、體重和頭髮顏色之類的，甚至還有時間這個維度。

 

因此，世間萬物都具有無數個維度。事實上在具體的問題中顯然並不需要考慮這無數個維度，只需分析具體問題所需要的維度。

比如說，一個導航的程式，人的身高、體重和頭髮顏色是無所謂的，而經度和緯度是導航程式最關心的兩個基礎維度，此外還有方向、速度等等維度是和導航相關的，總之具體問題具體分析。

 

現在聯想一下高階語言裡陣列，如果把多維陣列各個維度拿出來看，是不是與物理上的“維度”的概念有種異曲同工之妙？

• • • • int dp[n₀][n₁][n₂];

比如上面這個多維陣列每個維度n₀、n₁和n₂都可以自由在0到n_i-1變化，這正是維度的概念！只不過這些維度是些表面沒有太多意義的連續非負整數。

 

如果我們賦予它們意義呢？請看下一節，【狀態】。

 

 

二、狀態

---

事物具有多個維度，反之多個維度就能共同描述一個事物，而多個維度的值就描述了事物的狀態。

比如說，導航程式，經度和緯度這兩個維度的值就能描述當前某使用者的狀態，即這個使用者正在某經度某維度的地方。

 

對應於陣列，經度、緯度兩個維度對應了二維陣列：

• • • • int dp[MaxLng][MaxLat];

 

如果多維陣列各個維度的值確定後，那麼就相當於確定了在多維陣列中具體哪一個單元格。因此可以這麼說，各個單元格就對應了各個狀態，陣列就是狀態的集合，而狀態就是通過確定陣列各個維度的值定位的！

• • • • dp[x][y]所對應的單元格就表示人在經度x緯度y的狀態

 

不過，單元格可不僅僅是單元格，因為陣列可以是bool型別、int型別等等，即這個單元格有值的。這個值就是狀態的值，而狀態該是什麼型別的值，取值是多少這取決於具體的問題。

注意，上面說到值有兩個，紅色字，一個是維度的值，一個是狀態的值，其中維度的值描述了具體的狀態。

比如說，上面的導航程式的陣列是int型別，這樣dp[x][y]就可以拿來表示人在到達經度x緯度y這個狀態所需的時間（分鐘數）。

再比如說，如果陣列是bool型別，這樣dp[x][y]就可以拿來表示人能否到達經度x緯度y這個狀態。

 

在動態規劃問題裡，狀態的值經常是最小值、最大值和方案數等。一般就是從已知的初始狀態的值，通過狀態的轉移，得出最終目標狀態的值。

不過，上面提到的這個“狀態”還不是動態規劃裡的“狀態”，因為還少了一樣東西——請看下一節，【無後效性】。

 

 

三、無後效性

---

動態規劃的狀態必須是無後效性的。下面我用一道題目具體說明什麼是無後效性。

 

HDU2041 超級樓梯

有一樓梯共M級，剛開始時你在第一級，若每次只能跨上一級或二級，要走上第M級，共有多少種走法？

 

這個問題裡面很容易找到一個維度：樓梯的級數。那麼到達第i級臺階就是一個狀態，簡稱狀態i，問題所需要求的是到達狀態i的方案數，即：

• • • • dp[i]表示到達第i級臺階的方案數

 

i的取值是從1到M，也就是說有M個狀態。這M個狀態之間是有關係的。比如可以從第1級的臺階直接移動到第2級或者第3級，或者第5級臺階可以從第3級或者第4級臺階直接移動到。

 

下面就M取5畫一張狀態圖：

 

 

 

這張圖上面的頂點表示的是各個狀態，有向邊（弧）就表示狀態的轉移。事實上這張圖是一張有向無環圖（DAG, Directed Acyclic Graph），即從任何一點出發不可能回到自身。

也就是說在那張圖中狀態i是通過狀態i-1和狀態i-2確定的，並且和狀態i-3、i-4、i-5...沒有一點關係，之後狀態i也不會影響到狀態i-3、i-4、i-5…，i-3、i-4、i-5狀態的值已經是確定好的。

 

這就是無後效性。動態規劃的狀態必須是無後效性的狀態。

 

動態規劃本質上可以理解成在一個DAG上的遞推：入度0的狀態點就是初始的狀態，有向邊說明了狀態轉移的方向，通過狀態的轉移按著DAG的拓撲序推出最終目標狀態的值。而由於是DAG，狀態不會重複經過，最多就經過所有的狀態。

 

具體如何轉移請看下一節，【狀態轉移】。

 

 

四、狀態轉移

---

前面提到了，動態規劃的過程就是從初始狀態轉移到最終的目標狀態，而初始狀態的值是知道的，目標狀態的值就是問題需要的。

 

還是那一題【超級樓梯】，狀態（的值）是這麼表示的：

• • • • dp[i]表示到達第i級臺階的方案數

 

而轉移的表示，通常當然不是畫圖，而是寫出狀態轉移方程：

• • • • dp[i] = 1 （i=1）
      • dp[i] = dp[i-1] （i=2）
      • dp[i] = dp[i-1] + dp[i-2] （i>2）

 

為什麼是這樣呢？可以從之前畫的狀態圖中理解。

1. 首先dp[1]就表示到達臺階1的方案數，一開始就在臺階1，這個狀態的值當然就是1了，即dp[1]=1，而事實上這個也正是初始狀態；
2. 然後dp[i]=dp[i-1]（i=2），也就是說dp[2]=dp[1]，因為走到臺階2只有一種策略就會從臺階1走來，因而到達臺階2的方案數就等於達到臺階1的方案數，也就是1；
3. 最後dp[i]=dp[i-1]+dp[i-2]（i>2），這個從語義上理解是這樣的：走到i-1的方案數是dp[i-1]，然後向上走一步就到了i，因而狀態i的方案數就有dp[i-1]；而走到i-2的方案數是dp[i-2]，然後向上走2步就到了i，因而狀態i的方案數又可以有dp[i-2]種；總共就是dp[i-1]+dp[i-2]個方案數。

 

那麼有了狀態轉移方程，就可以動手寫程式實現了。具體程式的實現多種多樣，但要注意的是狀態的值一定要按拓撲序依次求出。下面我講講講三種方式：“人人為我”、“我為人人”和記憶化搜尋。其中“人人為我”和“我為人人”這兩個是我從北大ACM-ICPC暑期課的課件中學到的。

 

• “人人為我”

　　這個很常見，就是上面轉移方程表示的那樣。

　　狀態圖大概可以這麼看：

　

 

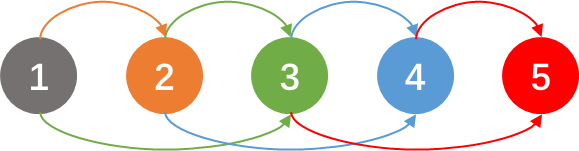
　　比如可以看到狀態5就是從3和4轉移過來的。

　　寫成程式就是這樣：

1. #include<cstdio>
2. using namespace std;
3.  
4. int dp[41];
5.  
6. int main(){
7.  
8. dp[1]=1; dp[2]=1;
9. for(int i=3; i<=40; ++i){
10. dp[i]=dp[i-1]+dp[i-2];
11. }
12.  
13. int N,M;
14. scanf("%d",&N);
15. while(N--){
16. scanf("%d",&M);
17. printf("%d\n",dp[M]);
18. }
19. return 0;
20. }

　　

 

• “我為人人”

　　這個是從當前狀態順著推過去，更新能到達狀態的值。

　　這個實現起來挺直觀的，因為是順著往前推。

　　狀態圖可以這麼看：

　　比如可以看到狀態1更新到2和3。

　　寫成程式是這樣的：

1. #include<cstdio>
2. using namespace std;
3.  
4. int dp[44];
5.  
6. int main(){
7.  
8. dp[1]=1;
9. for(int i=1; i<40; ++i){
10. dp[i+1]+=dp[i];
11. dp[i+2]+=dp[i];
12. }
13.  
14. int N,M;
15. scanf("%d",&N);
16. while(N--){
17. scanf("%d",&M);
18. printf("%d\n",dp[M]);
19. }
20. return 0;
21. }

 

 

• 記憶化搜尋

一般都是用DFS實現，就是用搜尋當前狀態能從哪兒轉移過來。

另外開一個陣列記錄搜尋過的狀態的值，避免重複搜尋，時間複雜度就不會是指數級的了，而是多項式級。

有時候用記憶化搜尋很直觀，而且記憶化搜尋還可以避免搜尋無意義、不需要的狀態，從而使效率提升。

這個直接上程式碼吧：

1. #include<cstdio>
2. using namespace std;
3.  
4. int dp[44];
5.  
6. int dfs(int i){
7. if(dp[i]!=0) return dp[i];
8. return dp[i]=dfs(i-1)+dfs(i-2);
9. }
10.  
11. int main(){
12. dp[1]=1; dp[2]=1;
13.  
14. int N,M;
15. scanf("%d",&N);
16. while(N--){
17. scanf("%d",&M);
18. printf("%d\n",dfs(M));
19. }
20. return 0;
21. }