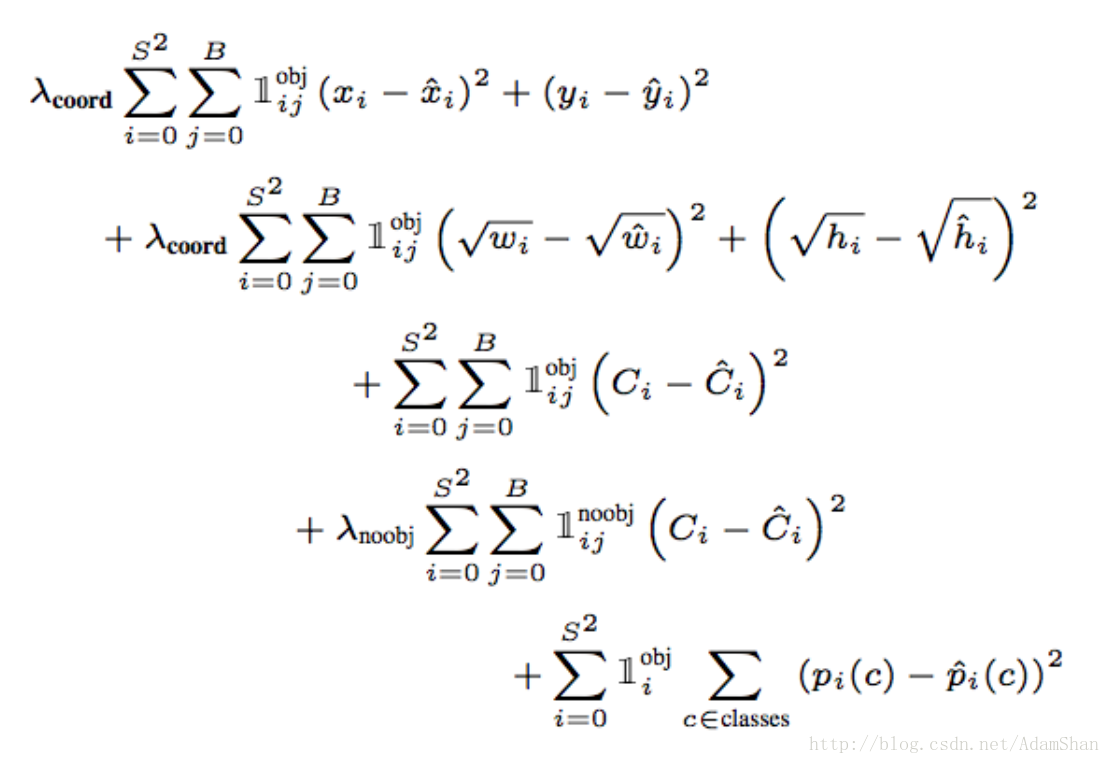無人駕駛汽車系統入門（十二）——卷積神經網路入門，基於深度學習的車輛實時檢測

上篇文章我們講到能否儘可能利用上影象的二維特徵來設計神經網路，以此來進一步提高識別的精度。在這篇部落格中，我們學習一類專門用來處理具有網格結構的資料的神經網路——卷積網路（Convolutional Network）。此外，我們使用keras來實現一種深層卷積網路——YOLO，使用YOLO對車輛進行實時檢測。

創作不易，轉載請註明出處：http://blog.csdn.net/adamshan/article/details/79193775

什麼是卷積，卷積的動機

卷積運算

卷積是一種特殊的線性運算，是對兩個實值函式的一種數學運算，卷積運算通常用符號 $*$ 來表示，我們以Kalman濾波中的例子為例，來討論一個一維離散形式的卷積：

假設我們的可回收飛船正在著陸，其感測器不斷測量自身的高度資訊，我們用 $h(i)$ 來表示 $i$ 時刻的高度測量，這個測量是以一定的頻率發生的（即每隔一個時間間隔測量一次，所以測量 $h(i) 是離散的$），受限於感測器，我們知道測量是不準確的，所以我們採用一種加權平均的方法來簡單處理，具體來說，我們可以認為：越接近於時刻 $i$ 的測量，越符合時刻 $i$ 時的真實高度，即我們給測量 $s(i) = w_ih(i) + w_{i-1}h(i-1) + w_{i-2}h(i-2)...$ 其中的權重 $w_i > w_{i-1} >w_{i-2} ...$ 。這就是一個一維離散形式的卷積，由於這個例子中我們不可能得到“未來的測量”，所以只包含了一維離散卷積的一半，下面是一維離散卷積的完整公式：

$s(i) = (h*w)(i) = \sum_{j=-\infty}^{\infty}h(j)w(i-j)$

其中 $i$ 表示我們計算的狀態(時刻，位置)，$j$ 表示到狀態 $i$ 的距離（可以是時間差，空間距離等等），這裡的 $h$ 和 $w$ 就分別表示兩個實值函式。在卷積神經網路的術語中，第一個函式 $h$ 被稱為輸入，第二個函式 $w$ 被稱為 核函式（kernal function） , 輸出 $s$ 被稱為 特徵對映（feature map），很顯然，在實際的例子中，$j$ (即我們考量的區間)一般不會是負無窮大到正無窮大，它通常是個很小的範圍。在深度學習的應用中，輸入通常是高維度的陣列（比如說影象），而核函式也是由演算法（如隨機梯度下降）產生的高維引數陣列。如果輸入二維影象 $I$ ,那麼相應的我們也需要使用二維的核 $K$，則這個二維卷積可以寫為：

$S(m. n) = (I * K)(m, n) = \sum_i\sum_jI(i, j)K(m-i, n-j)$

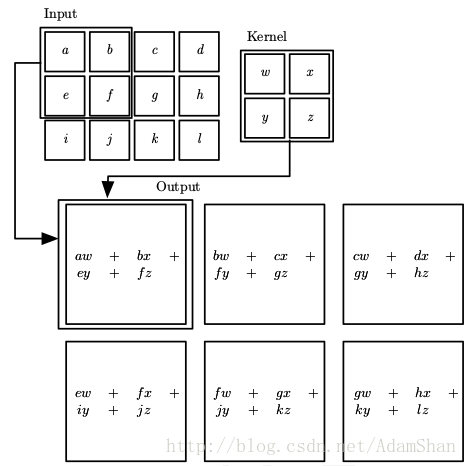
其中，$(m, n)$ 是計算的畫素位置， $(i, j)$ 是考量的範圍。我們用更加直觀的形式來表示的話，二維卷積如下所示：

卷積的動機

那麼在回答了什麼是卷積以後，我們看看為什麼使用卷積這種線性運算。首先我們看看卷積神經網路的定義：

卷積神經網路是指在網路中至少使用了一層卷積運算來代替一般的矩陣乘法運算的神經網路。

我們知道，全連線層中的輸入邊實際上是乘權重再累加，即本質上是一個矩陣乘法，那麼卷積層實際上就是用卷積這種運算替代了原來全連線層中的矩陣乘法，卷積的出發點是通過下述三種思想來改進機器學習系統：

• 稀疏互動(sparse interactions)
• 引數共享(parameter sharing)
• 等變表示(equivariant representations)

稀疏互動

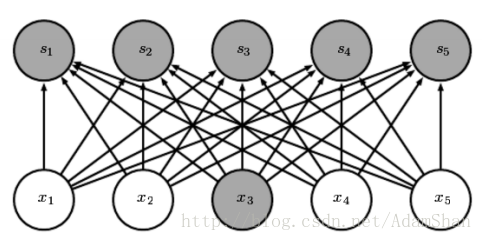
對於普通的全連線網路，層與層之間的節點是全連線的：

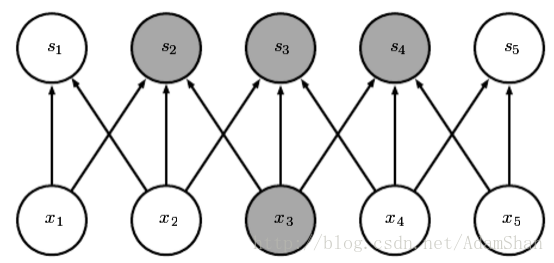
但是對卷積網路而言，下一層的節點只與其卷積核作用到的節點相關：

(圖片出處： Goodfellow et al. Deep learning. 2016.)

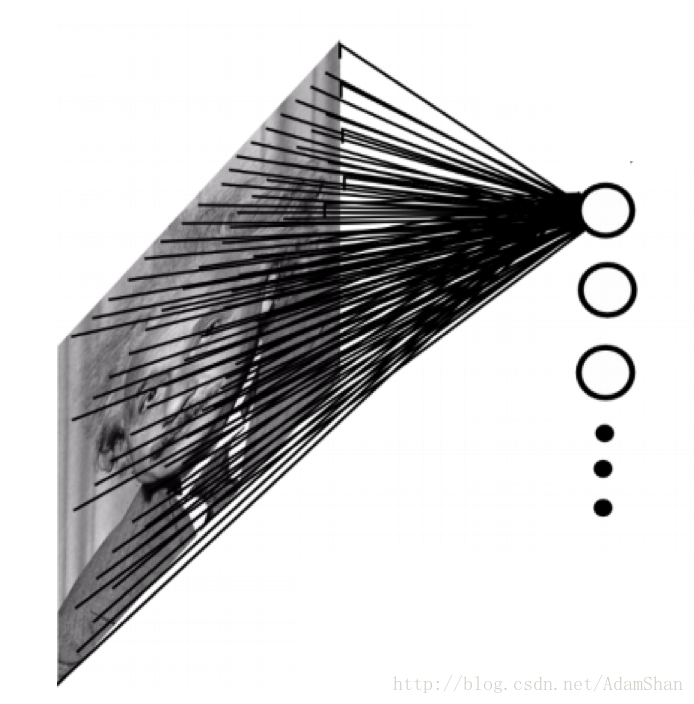
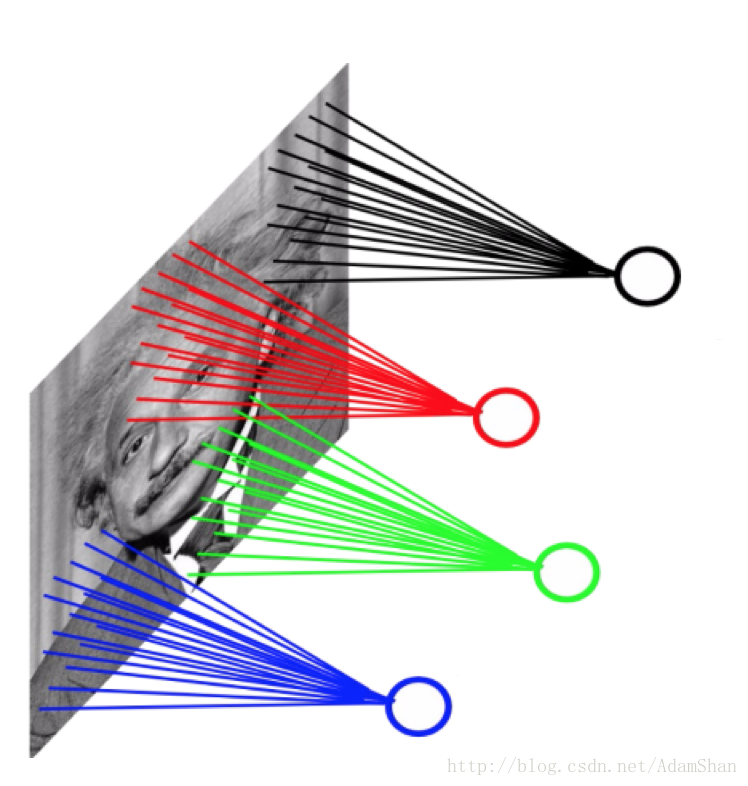
使用稀疏連線的一個直觀的好處就是網路的引數更少了，我們以一副 $200 \times 200$ 的灰度圖為例，當將它輸入到全連線的神經網路中時，如下：

假設這個網路的的第一個隱含層有4萬個神經元（對於輸入樣本為40000維的情況來說，40000個隱含層節點是合適的），那麼這個網路光這一層就有接近20億個引數。這樣的模型訓練的計算量是非常大的，且需要很大的儲存空間。

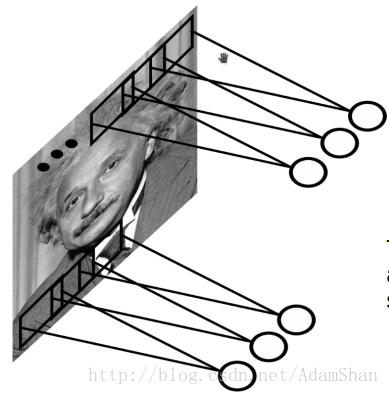
對於卷積網路而言，情況如下：

這裡我們仍然使用40000個隱含層神經元，我們的卷積核（也被稱為濾波(Filter)）的大小為 $10 \times 10$ ,這樣的一層卷積的引數量只有約4000000個，引數數量遠遠小於全連線的網路。

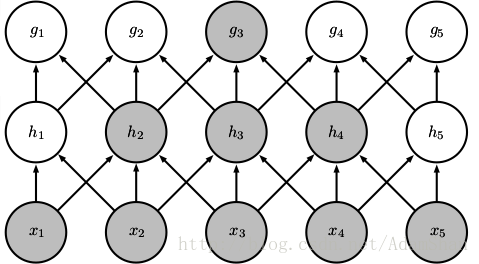
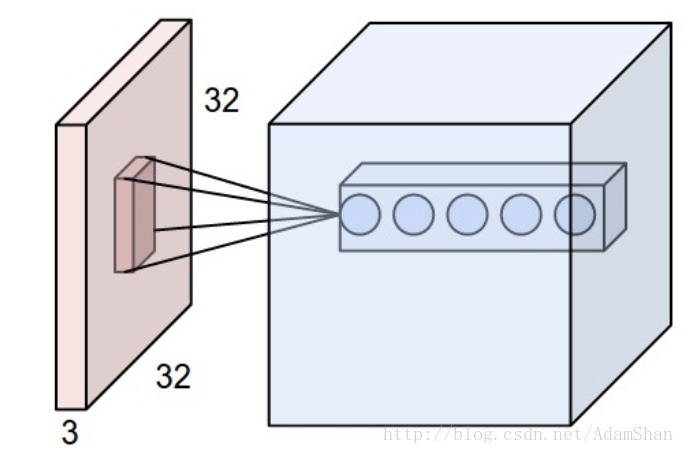
讀者可能會有疑問？卷積的輸出只與輸入的區域性產生關聯，如果某種規律並不是建立在區域性特徵之上，而是和整個輸入都有關聯，那麼通過卷積建立起來的表示是不是就不完整呢？並非如此。現代的卷積網路往往需要疊加多個卷積層，卷積網路雖然在直接連線上是稀疏的，但是在更深的層中的單元可以間接的連線到全部的或者大部分的輸入影象，如下圖所示：

提示：在卷積網路的相關文獻中，存在術語：神經元（neuron），核（kernal），濾波（filter），它們都指同一個事物——核函式，在本文中，我們統一稱為卷積核。

引數共享

使用卷積核實際上就是卷積網路的引數，卷積核在輸入影象上滑動視窗，這也就意味著輸入的影象的畫素點共享這一套引數，如下圖所示：

卷積網路中的引數共享使我們只需要學習一個引數集合，而不需要對每一個畫素都學習一個單獨的引數集合，它使得模型所需的儲存空間大幅度降低。

等變表示

由於整個輸入圖片共享一組引數，那麼模型對於影象中的某些特徵平移具有 等變性 。那麼，何謂等變呢？

如果函式 $f(x)$ 和函式 $g(x)$ 滿足：

$f(g(x)) = g(f(x))$

那麼我們稱函式 $f$ 對變換 $g$ 具有等變性。同理，平移就是函式 $g$ ，那麼如果我們平移輸入的物件，那麼輸出中建立的表示也會平移相同的量，這一性質在檢測輸入中的某些共有結構（比如說邊緣）是非常有用的，尤其在卷積神經網路的前幾層（靠近輸入的層）。

卷積神經網路

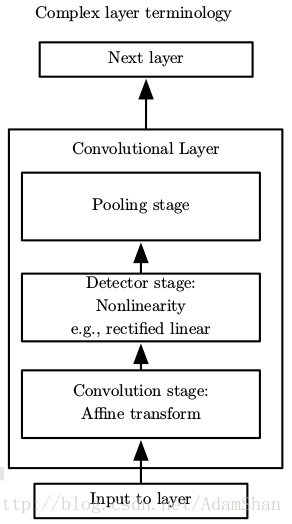
下圖是一個典型的卷積神經網路層（我們簡稱卷積層）,傳統的卷積層包含如下三個結構：

• 卷積運算
• 啟用函式（非線性變換）
• 池化（Pooling）

這裡的啟用函式起著與全連線網路一樣的作用，$ReLU$ 是最常用的啟用函式，下面我們來詳細討論一下池化。

池化

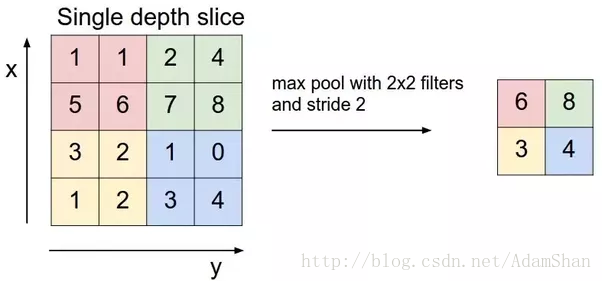
池化通常也被稱為池化函式，池化函式的定義就是：一種使用相鄰位置的總體統計特徵來替換該位置的值，池化的理念有點向時序問題中的滑動視窗平均。下圖表示一種池化方法——最大池化（maxpooling）：

上圖表示一個2×2的最大池化，其步幅（Stride）為2,我們可以理解為，使用一個 $2 \times 2$ 的視窗，以2為步長在輸入影象上滑動視窗，計算視窗之內輸入元素的最大值並輸出。我們不難發現，經過這樣一個池化函式以後，輸入的尺寸被“壓縮”了，同時，池化並沒有引入額外的引數，即池化能夠降低輸入的尺寸，也就意味著我們在後面的卷積層中需要的引數更少，因此，在使用池化以後，整個神經網路的引數數量會進一步降低。下面是池化的輸入輸出的尺寸計算公式：

假設輸入的尺寸為：$w \times h \times d$，步幅為 $s$ ，視窗的大小為 $f \times f$ ，則輸出的寬，高和深度分別為：

$w_{out} = \frac{(w-f)}{s} + 1$

$h_{out} = \frac{(h-f)}{s} + 1$

$d_{out} = d$

常用的池化函式主要有最大池化（Max Pooling）和平均池化（Average Pooling），分別是輸出相鄰的矩陣區域的最大值和平均值，不論是哪種池化，都對於輸入的影象中的目標的少量平移具有不變性，即輸入中的目標物件發生少量的平移，池化函式的輸出不會發生改變。當我們對於卷積的輸出進行池化時，由於卷積學習的是分離的特徵（比如底層的卷積學習到的是各種邊緣特徵），特徵可能存在一些變換（平移，旋轉等等），新增池化函式，能夠進一步學習到應該對哪些變換具有不變性。

卷積的一些細節

我們前面大致瞭解了什麼是卷積，在卷積神經網路中，卷積計算還有一些細節問題要考慮。

填充和輸入輸出尺寸

首先，就是輸入輸出的尺寸換算。和前面的池化一樣，我們假設輸入的尺寸為 $w \times h \times d$，卷積的步幅為 $s$ ，卷積核的大小為 $f \times f \times d$ ，卷積網路中往往還有一個處理方法，叫做填充(padding)，如果我們不想讓我們的卷積核越過影象的邊界去滑動的話，我們稱之為 有效填充（valid padding） ，令 $p$ 為填充的畫素數，則使用有效填充來處理邊界時 $p = 0$ ，然而，在卷積網路的前幾層中，我們要儲存儘可能多的原始輸入資訊，以便我們可以提取這些低階特徵。我們想要應用同樣的卷積層，但我們想將輸出量保持與輸入相同的寬高，為了做到這一點，我們使用一定數量的0填充在邊界的周圍，使得卷積的輸出和輸入有著相同的寬高，我們稱之為 相同填充（same padding）。輸出的寬，高和深度的計算為：

$w_{out} = \frac{(w-f + 2p)}{s} + 1$

$h_{out} = \frac{(w-f + 2p)}{s} + 1$

$d_{out} = k$

其中， $k$ 表示卷積核的個數。

卷積核的深度

通常來說，我們回使用多個卷積核，如下圖所示：

不同的核學習不同的特徵，有些核可能學習的是一些顏色特徵，有些核可能學習的是一些邊緣，形狀特徵，下圖是同一層中已經訓練好的卷積神經網路的核視覺化效果（Krizhevsky et al.）

卷積核的數量我們成為卷積核的深度。

LeNet

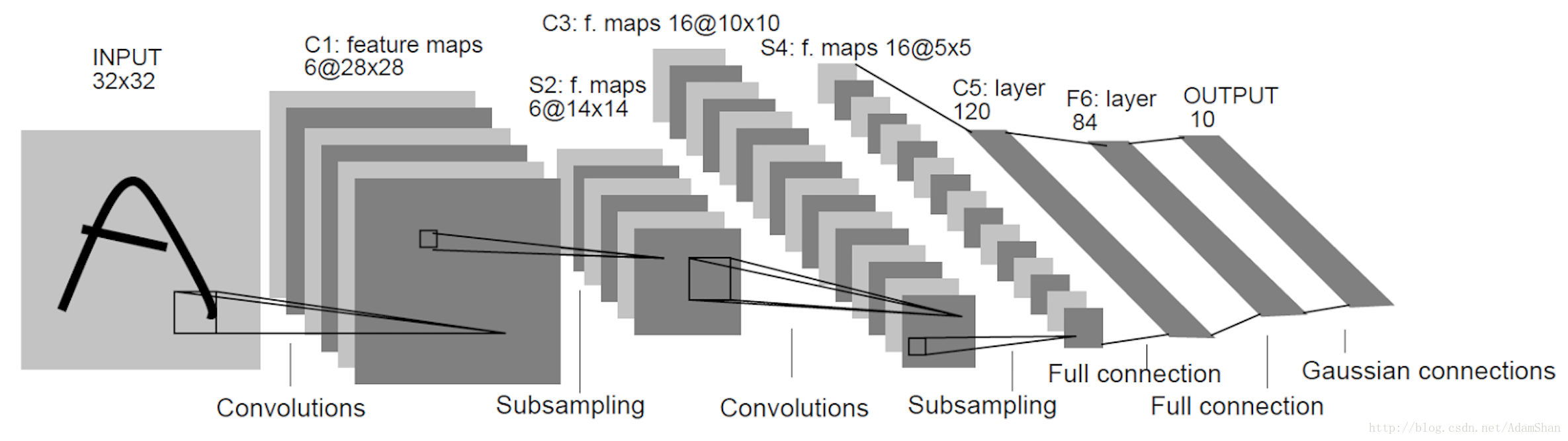
下圖是LeNet是LeCun等人在1998年提出的用於解決手寫字識別的卷積網路，其整體結構如下：

我們從LeNet出發來了解卷積網路的設計模式。如圖，卷積網路通常使用金字塔形結構，即隨著層數的增加，輸出的深度不斷增加，同時，我們使用諸如池化，valid padding和大步幅來縮小輸出的寬高尺寸。同時，卷積核的尺寸選擇已有一定的技巧，通常來說，我們往往在靠近輸入的卷積層中使用較大的卷積核以縮小輸出的尺寸（如 $7 \times 7$ ），而在後面的卷積層中使用小卷積核以充分建立特徵表示（如 $3 \times 3$ ）。

卷積網路的末端和前饋神經網路類似，我們將最後一個卷積層的輸出展成向量，輸入到一個多層感知機中，對於分類問題，仍然是使用交叉熵作為損失函式，使用隨機梯度下降等演算法訓練整個神經網路的引數。

卷積神經網路的視覺化例子：http://scs.ryerson.ca/~aharley/vis/conv/

基於YOLO的實時車輛檢測

YOLO（you only look once） 是一種目標檢測模型。在深度學習出現之前，傳統的目標檢測方法的步驟主要是：

• 提取目標的特徵（Hist，HOG，SIFT等）
• 訓練對應的分類器（訓練一個能判斷一張影象是否為目標的分類器，由於是二分類任務，所以通常使用SVM）
• 滑動視窗搜尋
• 重複和誤報過濾

其主要問題有兩方面：一方面滑窗選擇策略沒有針對性、時間複雜度高，視窗冗餘；另一方面手工設計的特徵魯棒性較差，分類器不可靠。

自深度學習出現之後，目標檢測取得了巨大的突破，最矚目的兩個方向有：1 以RCNN為代表的基於Region Proposal的深度學習目標檢測演算法（RCNN，SPP-NET，Fast-RCNN，Faster-RCNN等）；2 以YOLO為代表的基於迴歸方法的深度學習目標檢測演算法（YOLO，SSD等）。我們介紹基於迴歸方法的深度學習目標檢測方法——YOLO，並且使用YOLO的tiny版本實現一個實時的車輛檢測DEMO。

YOLO

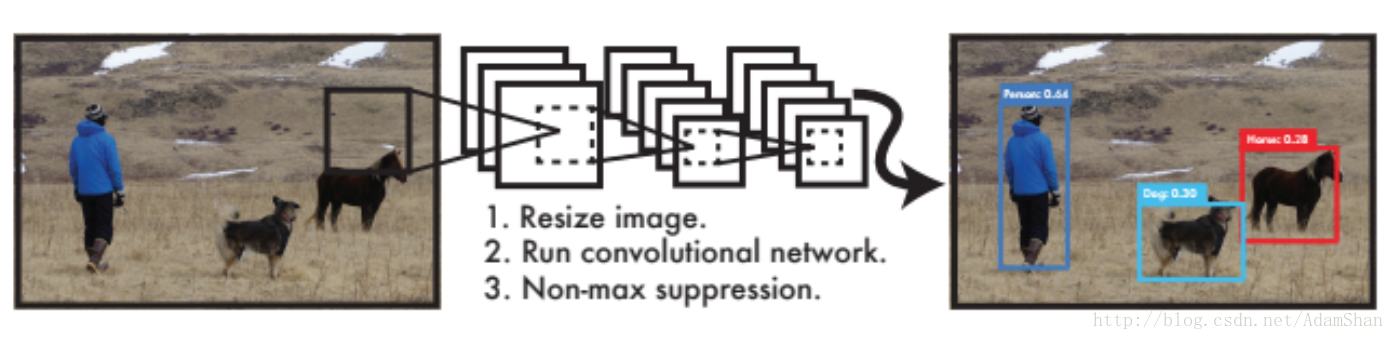
YOLO將目標檢測看作是一個迴歸問題，訓練好的網路的工作流程非常簡單，如下圖所示：

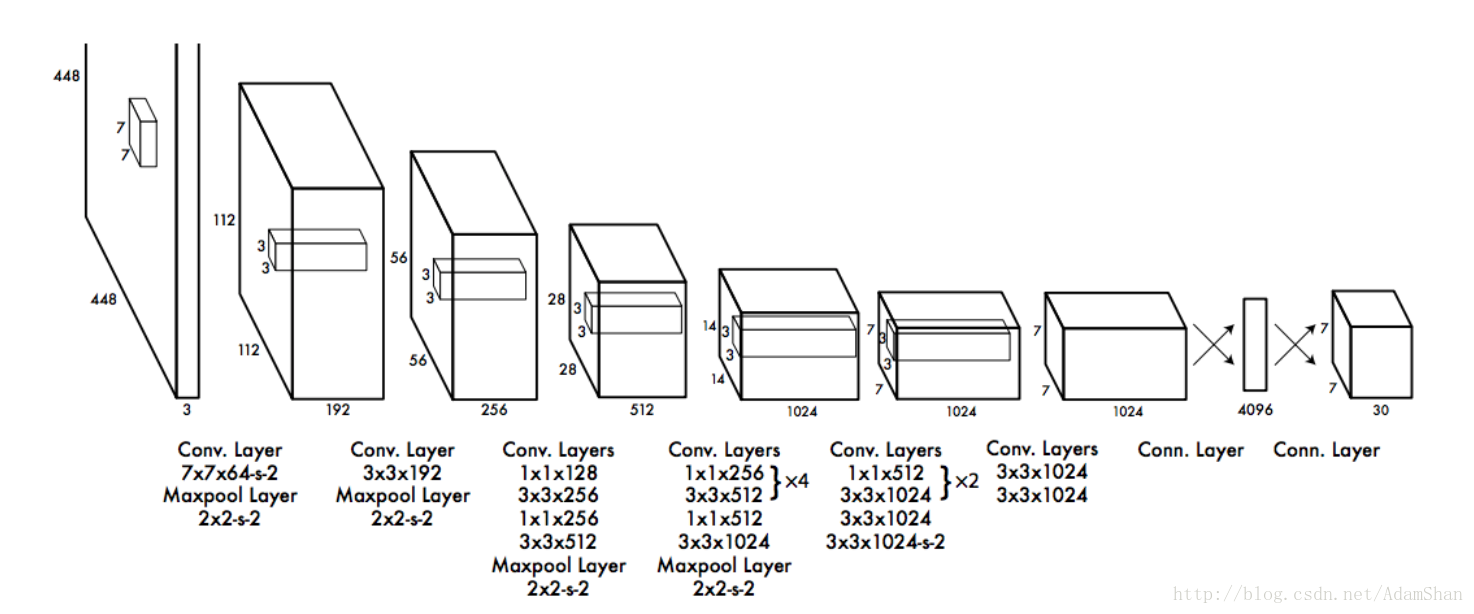
如圖，作為End-To-End網路，輸入原始影象，輸出即為目標的位置和其所屬類別及相應的置信概率。不同於傳統的滑動視窗檢測演算法,在訓練和應用階段，YOLO都使用的是整張圖片作為輸入。YOLO的具體網路結構如下：

整個網路包含了24個卷積層以及2個全連線層，以下是YOLO的整個流程：

預訓練分類網路

• 首先使用上圖中的前20個卷積層+一個平均池化層+一個全連線層在ImageNet資料集上訓練一個分類網路，這個網路的輸入為 $224 \times 224$，該模型在ImageNet2012的資料集上的top 5精度為 $88\%$ 。

訓練檢測網路

接著就是將訓練的分類網路用於檢測，在預訓練好的20個卷積層的後面再新增4個卷積層和2個全連結層（即結構圖中的後4個卷積層和最後兩個全連線層），在這裡，網路的輸入變成了 $448\times 448$ ， 輸出是一個 $7\times 7\times 32$ 的張量。

輸入到檢測網路的圖片首先會被resize成 $448\times 448$ ,然後被被分割成 $7\times 7$ 的網格。

網路的輸出 $7\times 7\times 30$ 負責這7*7個網格的迴歸預測。我們來看看這每個網格的30個輸出構成：

每個網格都要預測2個bounding box，bounding box即我們用來圈出目標的矩形（也就是目標所在的一個矩形區域），一個bounding box包含如下資訊：

• 中心座標 $(x, y)$ ,即我們要預測的目標的所在的矩形區域的中心的座標值。
• bounding box的寬和高 $(w, h)$
• 置信度（confidence）：代表了所預測的box中含有object的置信度和這個box預測的有多準兩重資訊

每個網格都要預測兩個bounding box，即10個輸出，此外，還有20個輸出代表目標的類別，YOLO論文在訓練時一共檢測20類物體，所以一共有20個類別的輸出,我們記做 $C$ ，合集每個網格的預測輸出有30個數值。

損失函式

要很好地迴歸出這30個數值，損失函式的設計就必須在bounding box座標，寬高，置信，類別之間達到一個很好的平衡。YOLO使用如下函式作為檢測網路的損失函式：

測試

在測試階段，每個網格預測的類別資訊和bounding box預測的confidence相乘，就得到每個bounding box的class-specific confidence score。那麼對整個影象的每個網格都做這種操作，則可以得到 $7 \times 7 \times 2 = 98$ 個bounding box，這些bounding box既包含座標等資訊也包含類別資訊。

得到每個bbox的class-specific confidence score以後，設定閾值，濾掉得分低的boxes，對保留的boxes進行NMS處理，就得到最終的檢測結果。

NMS（Non-maximum suppression）:非最大抑制，它首先基於物體檢測分數產生檢測框，分數最高的檢測框M被選中，其他與被選中檢測框有明顯重疊的檢測框被抑制。在本例中，使用YOLO網路預測出一系列帶分數的預選框，當選中最大分數的檢測框M，它被從集合B中移出並放入最終檢測結果集合D。於此同時，集合B中任何與檢測框M的重疊部分大於重疊閾值Nt的檢測框也將隨之移除。

基於YOLO的車輛檢測程式碼

由於車輛檢測對實時性要求高，我們使用一種YOLO的簡化版本：Fast YOLO，該模型使用簡單的9層卷積替代了原來的24層卷積，它犧牲了一定的精度，處理速度更快，從YOLO的45fps提升到155fps。滿足實時目標檢測的需求。

使用Keras實現fast YOLO網路結構：

model = Sequential()
model.add(Convolution2D(16, 3, 3,input_shape=(3,448,448),border_mode='same',subsample=(1,1)))
model.add(LeakyReLU(alpha=0.1))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Convolution2D(32,3,3 ,border_mode='same'))
model.add(LeakyReLU(alpha=0.1))
model.add(MaxPooling2D(pool_size=(2, 2),border_mode='valid'))
model.add(Convolution2D(64,3,3 ,border_mode='same'))
model.add(LeakyReLU(alpha=0.1))
model.add(MaxPooling2D(pool_size=(2, 2),border_mode='valid'))
model.add(Convolution2D(128,3,3 ,border_mode='same'))
model.add(LeakyReLU(alpha=0.1))
model.add(MaxPooling2D(pool_size=(2, 2),border_mode='valid'))
model.add(Convolution2D(256,3,3 ,border_mode='same'))
model.add(LeakyReLU(alpha=0.1))
model.add(MaxPooling2D(pool_size=(2, 2),border_mode='valid'))
model.add(Convolution2D(512,3,3 ,border_mode='same'))
model.add(LeakyReLU(alpha=0.1))
model.add(MaxPooling2D(pool_size=(2, 2),border_mode='valid'))
model.add(Convolution2D(1024,3,3 ,border_mode='same'))
model.add(LeakyReLU(alpha=0.1))
model.add(Convolution2D(1024,3,3 ,border_mode='same'))
model.add(LeakyReLU(alpha=0.1))
model.add(Convolution2D(1024,3,3 ,border_mode='same'))
model.add(LeakyReLU(alpha=0.1))
model.add(Flatten())
model.add(Dense(256))
model.add(Dense(4096))
model.add(LeakyReLU(alpha=0.1))
model.add(Dense(1470))

訓練YOLO網路是一個漫長的過程，這裡我們直接使用已經訓練好的模型，將模型引數載入到keras模型中，引數下載地址：https://drive.google.com/file/d/0B1tW_VtY7onibmdQWE1zVERxcjQ/view?usp=sharing
該下載連結需要科學上網，文末有訓練好的fast YOLO的百度網盤下載連結。

載入引數檔案到我們的網路中：

def load_weights(model, yolo_weight_file):
    tiny_data = np.fromfile(yolo_weight_file, np.float32)[4:]

    index = 0
    for layer in model.layers:
        weights = layer.get_weights()
        if len(weights) > 0:
            filter_shape, bias_shape = [w.shape for w in weights]
            if len(filter_shape) > 2:  # For convolutional layers
                filter_shape_i = filter_shape[::-1]
                bias_weight = tiny_data[index:index + np.prod(bias_shape)].reshape(bias_shape)
                index += np.prod(bias_shape)
                filter_weight = tiny_data[index:index + np.prod(filter_shape_i)].reshape(filter_shape_i)
                filter_weight = np.transpose(filter_weight, (2, 3, 1, 0))
                index += np.prod(filter_shape)
                layer.set_weights([filter_weight, bias_weight])
            else:  # For regular hidden layers
                bias_weight = tiny_data[index:index + np.prod(bias_shape)].reshape(bias_shape)
                index += np.prod(bias_shape)
                filter_weight = tiny_data[index:index + np.prod(filter_shape)].reshape(filter_shape)
                index += np.prod(filter_shape)
                layer.set_weights([filter_weight, bias_weight])

從YOLO網路的輸出中提取出車輛的檢測結果：

def yolo_net_out_to_car_boxes(net_out, threshold=0.2, sqrt=1.8, C=20, B=2, S=7):
    class_num = 6
    boxes = []
    SS = S * S  # number of grid cells
    prob_size = SS * C  # class probabilities
    conf_size = SS * B  # confidences for each grid cell

    probs = net_out[0: prob_size]
    confs = net_out[prob_size: (prob_size + conf_size)]
    cords = net_out[(prob_size + conf_size):]
    probs = probs.reshape([SS, C])
    confs = confs.reshape([SS, B])
    cords = cords.reshape([SS, B, 4])

    for grid in range(SS):
        for b in range(B):
            bx = Box()
            bx.c = confs[grid, b]
            bx.x = (cords[grid, b, 0] + grid % S) / S
            bx.y = (cords[grid, b, 1] + grid // S) / S
            bx.w = cords[grid, b, 2] ** sqrt
            bx.h = cords[grid, b, 3] ** sqrt
            p = probs[grid, :] * bx.c

            if p[class_num] >= threshold:
                bx.prob = p[class_num]
                boxes.append(bx)

    # combine boxes that are overlap
    boxes.sort(key=lambda b: b.prob, reverse=True)
    for i in range(len(boxes)):
        boxi = boxes[i]
        if boxi.prob == 0: continue
        for j in range(i + 1, len(boxes)):
            boxj = boxes[j]
            if box_iou(boxi, boxj) >= .4:
                boxes[j].prob = 0.
    boxes = [b for b in boxes if b.prob > 0.]

    return boxes

在測試圖片上的檢測結果：

在測試視訊上的效果：

YOLO 論文： https://pjreddie.com/media/files/papers/yolo.pdf

訓練好的Fast YOLO百度網盤下載連結：https://pan.baidu.com/s/1o9twnPo

完整程式碼下載連結：http://download.csdn.net/download/adamshan/10229339