莫隊演算法講解（含樹上莫隊）

莫隊演算法

莫隊演算法是一種離線演算法，通常不能有修改 操作。
其通過對詢問操作的執行順序進行更改，然後使用最暴力的方法，可以達到很好的複雜度。

首先，如果要用莫隊演算法，則必須滿足已知ans[l

,r]可以得到ans[l+1,r],ans[l-1,r],ans[l,r+1],ans[l,r-1]。

莫隊演算法的實現步驟為：
1、先對原序列進行分塊。
2、離線操作，對詢問進行排序，以左端點所在塊編號 為第一關鍵字，右端點的位置為第二關鍵字，進行排序。然後維護[l

,r]的答案，並不斷調整l和r。

我們來分析一下時間複雜度：
1、左端點所在塊編號確定時，右端點位置單調不下降，所以右端點移動最多造成的時間複雜度是O

(n)的，總共n√塊，總時間複雜度為O(nn√)。

2、左端點所在塊編號進行變動時，右端點移動最多造成的時間複雜度是O

(n)，總共n√塊，變動次數也就是n√次，總時間複雜度為O(nn√)。

3、塊內左端點位置每次最多移動n√

，一共m次詢問，也就是一共移動m次，總時間複雜度為O(mn√)。

總的來說，時間複雜度是32

次的，這是十分優秀的。

樹上莫隊

樹上莫隊是莫隊演算法的擴充，思想依然差不多，下面我介紹一種樹上莫隊的做法。

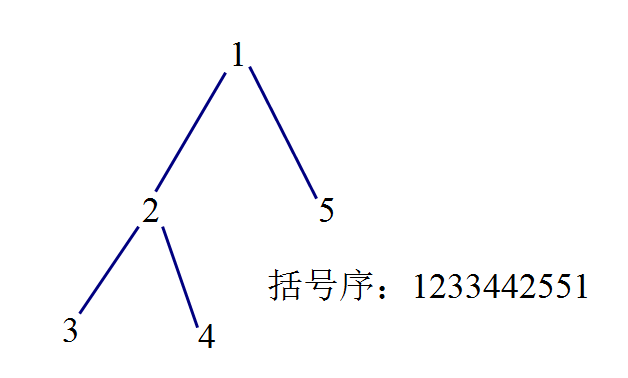
首先弄出樹的括號序。（對樹做一次深搜，第一次進入某節點時，將此節點編號加入序列，從某節點退出時，將此節點編號第二次加入序列）
如圖，有一棵樹，以及它的括號序：

然後記錄一個數在括號序中第一次出現和最後一次出現的位置。
如果要詢問j

到k之間路徑的資訊，需進行分類討論：
（以下均遵循此原則，出現兩次的數字不算入所求資訊中）
1、如果j是k的祖先，那麼所求資訊就為j和k最後出現的位置之間的資訊。
2、如果j不是k的祖先。那麼所求資訊就為j最先出現的位置以及k最後出現的位置之間的資訊，我們發現，j,k的lca不在其中，再把lca加上即可。

那麼實現的時候就是用cha

來表示一個點的出現情況的改變。
然後當做序列上的莫隊來做就可以了。

擴充：帶修改的莫隊

其實莫隊還是可以帶修改的。O(∩_∩)O~~
帶修改的莫隊其實也不難，我們三元組（l,r,x）來排序，x表示在此次詢問操作之前經過了x次修改操作。同樣的，知道(l

,r,x)的答案可以知道(l-1,r,x)(l+1,r,x)(l,r-1,x)(l,r+1,x)(l,r,x-1)(l,r,x+1)的答案，一樣可以用莫隊演算法。

塊大小需要設定為n23

，總時間複雜度是O(n53)，證明略。