計算機圖形學（二）輸出圖元_20_章節總結_程式展示_蝸形線、心形線、螺旋線

    蝸形線、心形線、螺旋線  

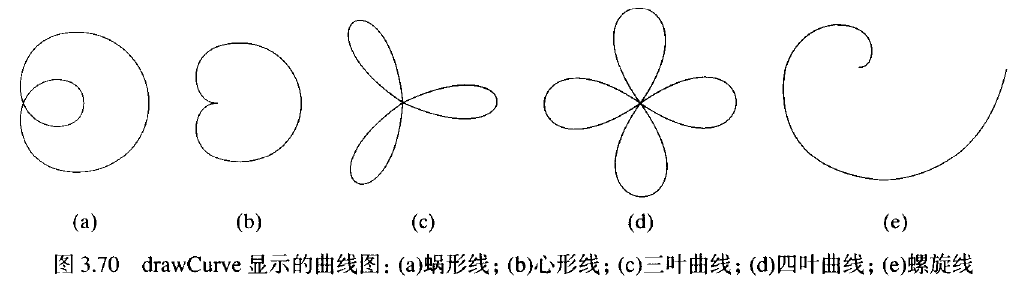
       最後一個程式顯示了圓公式的某些變化，其中使用了引數極座標方程(3.28)來計算曲線路徑的點。這些點用做顯示弧的逼近折線中直線段的端點。圖3.70中的弧通過圓半徑r的變化來生成。按照r的不同變化，可生成蝸形線、心形線、螺旋線或其他類似的圖形。

#include "stdafx.h"
#include "GL/glut.h"
#include "stdlib.h"
#include "math.h"
#include "iostream"
using namespace std;
struct screenPt
{
	GLint x;
	GLint y;
};
typedef enum { limacon = 1, cardioid, threeLeaf, fourLeaf, spiral } curveName;
GLsizei winWidth = 600, winHeight = 500;  //Initial display window size.


void init(void)
{
	glClearColor(1.0, 1.0, 1.0, 1.0);
	glMatrixMode(GL_PROJECTION);
	gluOrtho2D(0.0, 200.0, 0.0, 150.0);
}


void lineSegment(screenPt pt1, screenPt pt2)
{
	glBegin(GL_LINES);
	glVertex2i(pt1.x, pt1.y);
	glVertex2i(pt2.x, pt2.y);
	glEnd();
}


void drawCurve(GLint curveName)
{
	/* The limacon of Pascal is a modification of the circle equation
	* with the radius varying as r = a * cos (theta) + b, where a
	* and b are constants. A cardioid is a limacon with a = b.
	* Three-leaf and four-leaf curves are generated when
	* r = a * cos (n * theta), with n = 3 and n = 2, respectively.
	* A spiral is displayed when r is a multiple of theta.
	*/

	const GLdouble twoPi = 6.283185;
	const GLint a = 175, b = 60;
	GLfloat r, theta, dtheta = 1.0 / float(a);
	GLint x0 = 200, y0 = 250;     // Set an initial screen position.
	screenPt curvePt[2];
	glColor3f(0.0, 0.0, 0.0);    // Set curve position.
	curvePt[0].x = x0;          // Initialize curve position.
	curvePt[0].y = y0;


	switch (curveName){
	case limacon: curvePt[0].x += a + b; break;
	case cardioid: curvePt[0].x += a + a; break;
	case threeLeaf: curvePt[0].x += a;   break;
	case fourLeaf: curvePt[0].x += a;    break;
	case spiral:   break;
	default:       break;
	}

	theta = dtheta;
	while (theta < twoPi){
		switch (curveName){
		case limacon:
			r = a * cos(theta) + b;     break;
		case cardioid:
			r = a * (1 + cos(theta));   break;
		case threeLeaf:
			r = a * cos(3 * theta);     break;
		case fourLeaf:
			r = a * cos(2 * theta);     break;
		case spiral:
			r = (a / 4.0) * theta;       break;
		default:                         break;
		}

		curvePt[1].x = x0 + r * cos(theta);
		curvePt[1].y = y0 + r * sin(theta);
		lineSegment(curvePt[0], curvePt[1]);

		curvePt[0].x = curvePt[1].x;
		curvePt[0].y = curvePt[1].y;
		theta += dtheta;
	}
}


void displayFcn(void)
{
	GLint curveNum;
	glClear(GL_COLOR_BUFFER_BIT);     // Clear display window.
	cout << "\nEnter the integer value corresponding to\n";
	cout << "one of the following curve names.\n";
	cout << "Press any other key to exit.\n";
	cout << "\n1-limacon, 2-cardioid, 3-threeLeaf, 4-fourLeaf, 5-spiral: ";
	cin >> curveNum;

	if (curveNum == 1 || curveNum == 2 || curveNum == 3 || curveNum == 4 || curveNum == 5)
		drawCurve(curveNum);
	else
		exit(0);
	glFlush();
}


void winReshpeFcn(GLint newWidth, GLint newHeight)
{
	glMatrixMode(GL_PROJECTION);
	glLoadIdentity();
	gluOrtho2D(0.0, (GLdouble)newWidth, 0.0, (GLdouble)newHeight);
	glClear(GL_COLOR_BUFFER_BIT);
}
void main(int argc, char** argv)
{
	glutInit(&argc, argv);
	glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
	glutInitWindowPosition(100, 100);
	glutInitWindowSize(winWidth, winHeight);
	glutCreateWindow("Draw Curves");
	init();
	glutDisplayFunc(displayFcn);
	glutReshapeFunc(winReshpeFcn);
	glutMainLoop();
}

我在這裡輸入的是3。輸出3葉曲線形