機器學習-資料歸一化方法

拾毅者發表於2015-11-15
機器學習

本文主要介紹兩種基本的資料歸一化方法。

歸一化方法有兩種形式，一種是把數變為【0，1】之間的小數，一種是把有量綱表示式變為無量綱表示式。

資料標準化（歸一化）處理是資料探勘的一項基礎工作，不同評價指標往往具有不同的量綱和量綱單位，這樣的情況會影響到資料分析的結果，為了消除指標之間的量綱影響，需要進行資料標準化處理，以解決資料指標之間的可比性。原始資料經過資料標準化處理後，各指標處於同一數量級，適合進行綜合對比評價。

下面是歸一化和沒有歸一化的比較：

沒有經過歸一化，尋找最優解過程如下：


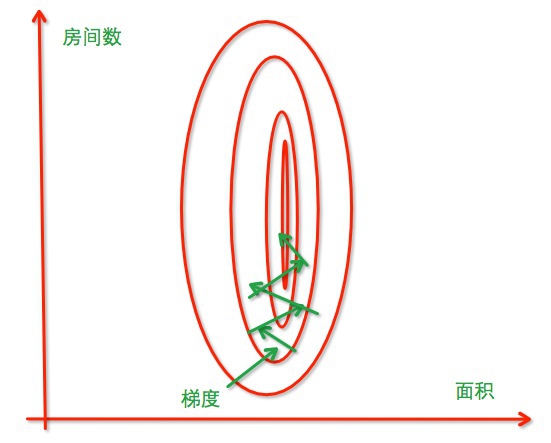
這裡寫圖片描述

經過歸一化，把各個特徵的尺度控制在相同的範圍內：


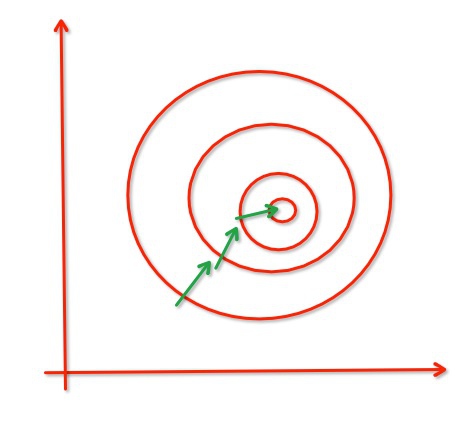
這裡寫圖片描述

從經驗上說，歸一化是讓不同維度之間的特徵在數值上有一定比較性，可以大大提高分類器的準確性。

以下是兩種常用的歸一化方法：

1.min-max標準化（Min-Max Normalization）

也稱為離差標準化，是對原始資料的線性變換，使結果值對映到[0 - 1]之間。轉換函式如下：

x∗=x−xminxmax−xmin
x^{*}=\frac{x-x_{min}}{x_{max}-x_{min}}

where，

xmin

x_{min}
表示樣本資料的最小值，xmax表示樣本數據的最大值
x_{max}表示樣本資料的最大值
。

Python程式碼實現：

def Normalization(x):
    return [(float(i)-min(x))/float(max(x)-min(x)) for i in x]

測試：

x=[1,2,1,4,3,2,5,6,2,7]
b=Normalization(x)

Output：

[0.0, 0.16666666666666666, 0.0, 0.5, 0.3333333333333333, 0.16666666666666666, 0.6666666666666666, 0.8333333333333334, 0.16666666666666666, 1.0]

如果想要將資料對映到[-1,1]，則將公式換成：

x∗=x−xmeanxmax−xmin
x^{*}=\frac{x-x_{mean}}{x_{max}-x_{min}}

x_mean表示資料的均值

Python程式碼實現：

import numpy as np
def Normalization2(x):
    return [(float(i)-np.mean(x))/(max(x)-min(x)) for i in x]

測試：

x=[1,2,1,4,3,2,5,6,2,7]
b=Normalization2(x)

Output：

[-0.3833333333333333, -0.21666666666666665, -0.3833333333333333, 0.1166666666666667, -0.049999999999999968, -0.21666666666666665, 0.28333333333333338, 0.45000000000000001, -0.21666666666666665, 0.6166666666666667]

注意：上面的Normalization是處理單個列表的。

2.z-score標準化方法

這種方法給予原始資料的均值（mean）和標準差（standard deviation）進行資料的標準化。經過處理的資料符合標準正態分佈，即均值為0，標準差為1，轉化函式為：

x∗=x−μσ
x^{*}=\frac{x-\mu}{\sigma}

其中，μ

\mu
表示所有樣本資料的均值，σ
\sigma
表示所有樣本的標準差。

Python程式碼實現：

import numpy as np
def z_score(x):
    x_mean=np.mean(x)
    s2=sum([(i-np.mean(x))*(i-np.mean(x)) for i in x])/len(x)
    return [(i-x_mean)/s2 for i in x]

測試：

x=[1,2,1,4,3,2,5,6,2,7]
print z_score(x)

Output:

[-0.57356608478802995, -0.32418952618453861, -0.57356608478802995, 0.17456359102244395, -0.074812967581047343, -0.32418952618453861, 0.42394014962593524, 0.67331670822942646, -0.32418952618453861, 0.92269326683291775]


此文乃博主即興之作，如果你從中有所收穫，歡迎前來贊助，為博主送上你的支援：【贊助中心】。
新浪微博： 【@拾毅者】

相關文章