經典手眼標定演算法之Tsai-Lenz的OpenCV實現

WHU_WG發表於2016-06-09
演算法AIOpenCV

       本文主要是講解經典手眼標定問題中的TSAI-LENZ 文獻方法，參考文獻為“A New Technique for Fully Autonomous and Efficient 3D Robotics Hand/Eye Calibration”，並且實現了基於OpenCV的C++程式碼程式，code可去CSDN資源下載，MATLAB版本作者為蘇黎世理工的Christian Wengert，也可在此處下載。

手眼標定問題描述

       在機器人校準測量、機器人手眼協調以及機器人輔助測量等領域，都要求知道機器人執行器末端（抓取臂）座標系和感測器（比如用來測量三維空間中目標位置和方向並固定在機器人手上的攝像機）座標系之間的相互關係，確定這種轉換關係在機器人領域就是通常所說的手眼標定。

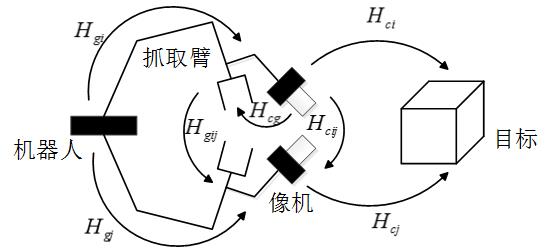
       將手眼標定系統如下圖所示，其中Hgij

H_{gij}
為機器人執行器末端座標系之間相對位置姿態的齊次變換矩陣；Hcij
H_{cij}
為攝像機座標系之間相對位置姿態的齊次變換矩陣；Hcg
H_{cg}
為像機與機器人執行器末端之間的相對位置姿態齊次矩陣。

手眼標定系統

       經過座標系變換，Hgij

H_{gij}
、Hcij
H_{cij}
和Hcg
H_{cg}
滿足如下關係：

HgijHcg=HcgHcij⇔(Rgij0Tgij1)(Rcg0Tcg1)=(Rcg0Tcg1)(Rcij0Tcij1)
{H_{gij}}{H_{cg}} = {H_{cg}}{H_{cij}} \Leftrightarrow \left( {\begin{array}{*{20}{c}} {{R_{gij}}}&{{T_{gij}}} \\ {\mathbf{0}}&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{R_{cg}}}&{{T_{cg}}} \\ {\mathbf{0}}&1 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{R_{cg}}}&{{T_{cg}}} \\ {\mathbf{0}}&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{R_{cij}}}&{{T_{cij}}} \\ {\mathbf{0}}&1 \end{array}} \right)

       將上式展開，可以得到手眼標定的基本方程：
{RgijRcg=RcgRcij(Rgij−I)Tcg=RcgTcij−Tgij
\left\{ {\begin{array}{*{20}{c}} {{R_{gij}}{R_{cg}} = {R_{cg}}{R_{cij}}} \\ {\left( {{R_{gij}} - I} \right){T_{cg}} = {R_{cg}}{T_{cij}} - {T_{gij}}} \end{array}} \right.

       因此，手眼標定問題也就轉化為從上述方程組中求解出Rcg
R_{cg}
和Tcg
T_{cg}
，下面就按照TSAI文獻所述求解該方程組。

“兩步法”手眼標定

       一般用“兩步法”求解基本方程，即先從基本方程上式求解出Rcg

R_{cg}
，再代入下式求解出Tcg
T_{cg}
。在TSAI文獻中引入旋轉軸-旋轉角系統來描述旋轉運動來進行求解該方程組，具體的公式推導可以檢視原始文獻，這裡只歸納計算步驟，不明白的地方可閱讀文獻，計算步驟如下：

Step1：利用羅德里格斯變換將旋轉矩陣轉換為旋轉向量

{rgij=rodrigues(Rgij)rcij=rodrigues(Rcij)
\left\{ {\begin{array}{*{20}{c}} {{r_{gij}} = rodrigues\left( {{R_{gij}}} \right)} \\ {{r_{cij}} = rodrigues\left( {{R_{cij}}} \right)} \end{array}} \right.

Step2：向量歸一化

⎧⎩⎨⎪⎪⎪⎪⎪⎪θgij=∥∥rgij∥∥2Nrgij=rgijθgijθcij=∥∥rcij∥∥2Nrcij=rcijθcij
\left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{\theta _{gij}} = {{\left\| {{r_{gij}}} \right\|}_2}}&{{N_{{r_{gij}}}} = \frac{{{r_{gij}}}}{{{\theta _{gij}}}}} \end{array}} \\ {\begin{array}{*{20}{c}} {{\theta _{cij}} = {{\left\| {{r_{cij}}} \right\|}_2}}&{{N_{{r_{cij}}}} = \frac{{{r_{cij}}}}{{{\theta _{cij}}}}} \end{array}} \end{array}} \right.

Step3：修正的羅德里格斯參數列示姿態變化

⎧⎩⎨⎪⎪⎪⎪Pgij=2sinθgij2NrgijPcij=2sinθcij2Nrcij
\left\{ {\begin{array}{*{20}{c}} {{P_{gij}} = 2\sin \frac{{{\theta _{gij}}}}{2}{N_{{r_{gij}}}}} \\ {{P_{cij}} = 2\sin \frac{{{\theta _{cij}}}}{2}{N_{{r_{cij}}}}} \end{array}} \right.

Step4：計算初始旋轉向量P′cg
P_{cg}^\prime

skew(Pgij+Pcij)Pcg′=Pcij−Pgij
skew\left( {{P_{gij}} + {P_{cij}}} \right){P_{cg}}^\prime = {P_{cij}}- {P_{gij}}

       其中，skew為反對稱運算，假設一個三維向量V=[vx;vy;vz]

V=[v_x;v_y;v_z]
，其反對稱矩陣為：

skew(V)=⎡⎣⎢0vz−vy−vz0vxvy−vx0⎤⎦⎥
skew\left( V \right) = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\text{0}} \\ {{v_z}} \\ { - {v_y}} \end{array}}&{\begin{array}{*{20}{c}} { - {v_z}} \\ {\text{0}} \\ {{v_x}} \end{array}}&{\begin{array}{*{20}{c}} {{v_y}} \\ { - {v_x}} \\ {\text{0}} \end{array}} \end{array}} \right]

Step5：計算旋轉向量Pcg
P_{cg}

Pcg=2Pcg′1+∣∣Pcg′∣∣2−−−−−−−−√
{P_{cg}} = \frac{{2{P_{cg}}^\prime }}{{\sqrt {1 + {{\left| {{P_{cg}}^\prime } \right|}^2}} }}

Step6：計算旋轉矩陣Rcg
R_{cg}

Rcg=⎛⎝1−∣∣Pcg∣∣22⎞⎠I+12(PcgPcgT+4−∣∣Pcg∣∣2−−−−−−−−√skew(Pcg))
{R_{cg}} = \left( {1 - \frac{{{{\left| {{P_{cg}}} \right|}^2}}}{2}} \right)I + \frac{1}{2}\left( {{P_{cg}}{P_{cg}}^T + \sqrt {4 - {{\left| {{P_{cg}}} \right|}^2}} skew\left( {{P_{cg}}} \right)} \right)

Step7：計算平移向量Tcg
T_{cg}

(Rgij−I)Tcg=RcgTcij−Tgij
\left( {{R_{gij}} - I} \right){T_{cg}} = {R_{cg}}{T_{cij}} - {T_{gij}}

演算法原始碼

       根據上述基本計算步驟，在利用OpenCV 2.0開源庫的基礎上，編寫Tsai手眼標定方法的c++程式，其實現函式程式碼如下：

void Tsai_HandEye(Mat Hcg, vector<Mat> Hgij, vector<Mat> Hcij)
{
    CV_Assert(Hgij.size() == Hcij.size());
    int nStatus = Hgij.size();

    Mat Rgij(3, 3, CV_64FC1);
    Mat Rcij(3, 3, CV_64FC1);

    Mat rgij(3, 1, CV_64FC1);
    Mat rcij(3, 1, CV_64FC1);

    double theta_gij;
    double theta_cij;

    Mat rngij(3, 1, CV_64FC1);
    Mat rncij(3, 1, CV_64FC1);

    Mat Pgij(3, 1, CV_64FC1);
    Mat Pcij(3, 1, CV_64FC1);

    Mat tempA(3, 3, CV_64FC1);
    Mat tempb(3, 1, CV_64FC1);

    Mat A;
    Mat b;
    Mat pinA;

    Mat Pcg_prime(3, 1, CV_64FC1);
    Mat Pcg(3, 1, CV_64FC1);
    Mat PcgTrs(1, 3, CV_64FC1);

    Mat Rcg(3, 3, CV_64FC1);
    Mat eyeM = Mat::eye(3, 3, CV_64FC1);

    Mat Tgij(3, 1, CV_64FC1);
    Mat Tcij(3, 1, CV_64FC1);

    Mat tempAA(3, 3, CV_64FC1);
    Mat tempbb(3, 1, CV_64FC1);

    Mat AA;
    Mat bb;
    Mat pinAA;

    Mat Tcg(3, 1, CV_64FC1);

    for (int i = 0; i < nStatus; i++)
    {
        Hgij[i](Rect(0, 0, 3, 3)).copyTo(Rgij);
        Hcij[i](Rect(0, 0, 3, 3)).copyTo(Rcij);

        Rodrigues(Rgij, rgij);
        Rodrigues(Rcij, rcij);

        theta_gij = norm(rgij);
        theta_cij = norm(rcij);

        rngij = rgij / theta_gij;
        rncij = rcij / theta_cij;

        Pgij = 2 * sin(theta_gij / 2)*rngij;
        Pcij = 2 * sin(theta_cij / 2)*rncij;

        tempA = skew(Pgij + Pcij);
        tempb = Pcij - Pgij;

        A.push_back(tempA);
        b.push_back(tempb);
    }

    //Compute rotation
    invert(A, pinA, DECOMP_SVD);

    Pcg_prime = pinA * b;
    Pcg = 2 * Pcg_prime / sqrt(1 + norm(Pcg_prime) * norm(Pcg_prime));
    PcgTrs = Pcg.t();   
    Rcg = (1 - norm(Pcg) * norm(Pcg) / 2) * eyeM + 0.5 * (Pcg * PcgTrs + sqrt(4 - norm(Pcg)*norm(Pcg))*skew(Pcg));

    //Computer Translation 
    for (int i = 0; i < nStatus; i++)
    {
        Hgij[i](Rect(0, 0, 3, 3)).copyTo(Rgij);
        Hcij[i](Rect(0, 0, 3, 3)).copyTo(Rcij);
        Hgij[i](Rect(3, 0, 1, 3)).copyTo(Tgij);
        Hcij[i](Rect(3, 0, 1, 3)).copyTo(Tcij);


        tempAA = Rgij - eyeM;
        tempbb = Rcg * Tcij - Tgij;

        AA.push_back(tempAA);
        bb.push_back(tempbb);
    }

    invert(AA, pinAA, DECOMP_SVD);
    Tcg = pinAA * bb;

    Rcg.copyTo(Hcg(Rect(0, 0, 3, 3)));
    Tcg.copyTo(Hcg(Rect(3, 0, 1, 3)));
    Hcg.at<double>(3, 0) = 0.0;
    Hcg.at<double>(3, 1) = 0.0;
    Hcg.at<double>(3, 2) = 0.0;
    Hcg.at<double>(3, 3) = 1.0;

}

相關文章