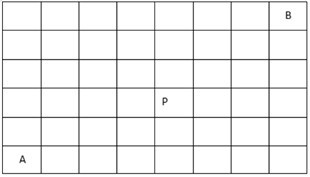
在如下8*6的矩陣中，請計算從A移動到B一共有____種走法。要求每次只能向上或向右移動一格，並且不能經過P。

jiafuLi2018發表於2017-05-26
矩陣

轉載別人的，供自己學習

【組合數學+動態規劃】在如下8*6的矩陣中，請計算從A移動到B一共有____種走法。要求每次只能向上或向右移動一格，並且不能經過P。

在如下8*6的矩陣中，請計算從A移動到B一共有__種走法。要求每次只能向上或向右移動一格，並且不能經過P。 

A:456 
B:492 
C:568 
D:626 
E:680 
F:702

解析: 
8*6的矩陣，從左下角A到右上角B，一共需要走12步，其中5步向上，7步向右，因此總的走法一共有C(12,5)=792種，但題目規定不能經過P，因此需要減去經過P點的走法。 
經過P的路徑分為兩部分，從A到P，從P到B。 
同理，從A到P的走法：C(6,2)=15； 
同理，從P到B的走法：C(6,3)=20； 
因此從A到B經過P點的走法有15*20=300種， 
所以從A到B不經過P點的走法有792-300=492種。

這題其實可以用程式算出來 
簡單的動態規劃 
dp[i][j] = dp[i][j-1] + dp[i-1][j];

程式碼如下:

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <string>

using namespace std;
int main()
{

  int dp[100][100] = {0};

  for(int i = 1; i <= 6; i++)
    for(int j = 1; j <= 8; j++)      
        dp[i][j] = dp[i-1][j] + dp[i][j-1];
    
    int dp2[100][100] = {0};
    dp2[0][1] = 1;

    for(int i = 1; i <= 4; i++)
        for(int j = 1; j <= 4; j++)
            dp2[i][j] = dp2[i-1][j] + dp2[i][j-1];

    cout<<dp[6][8] - dp2[4][4] * dp[3][5]<<endl;

  return 0;
}


相關文章